Guest Post by Willis Eschenbach
Short Post. You can skip this if you understand the tidal force. Some folks seem confused about the nature of tidal forces. Today I saw this gem: “The tide raising force acts in both directions (bulge on each side in the simplistic model)” … the author of that statement may understand the tides, but that isn’t how tidal forces work, they don’t act in different directions.
To clarify the situation, let me give an example. Imagine three one-kilogram masses M1, M2, and M3, connected by a blue rope, that are in free-fall directly into the sun. Figure 1 shows the situation.
 Figure 1. Forces on three one-kilogram masses M1—M3, which are in free-fall straight towards the sun, and are connected by the blue rope. The equations at the bottom show the force of gravity on each of the three masses. The “tidal force” is the difference between two gravitational forces on two objects. Solar tidal forces on a 1-kg mass at the earth’s surface average about half a micronewton (µN, or 10-6 newtons), and the lunar tidal forces are about twice that, about a micronewton. By comparison, Earth’s gravity exerts a force of about 10 newtons on a 1-kg mass at the surface …
Figure 1. Forces on three one-kilogram masses M1—M3, which are in free-fall straight towards the sun, and are connected by the blue rope. The equations at the bottom show the force of gravity on each of the three masses. The “tidal force” is the difference between two gravitational forces on two objects. Solar tidal forces on a 1-kg mass at the earth’s surface average about half a micronewton (µN, or 10-6 newtons), and the lunar tidal forces are about twice that, about a micronewton. By comparison, Earth’s gravity exerts a force of about 10 newtons on a 1-kg mass at the surface …
Clearly, the gravitational force on M1 is greater than the force on M2, which in turn is greater than the force on M3. The difference between those two gravitational forces is the tidal force. There are two different tidal forces of interest in the diagram, which are GF1 – GF2, and GF2 – GF3. As a result of these tidal forces, as the three masses fall towards the sun. the near mass M1 moves the furthest, the far mass M3 moves the least, and the blue rope is always under tension.
For tidal forces on a theoretical planet, just imagine that the surface of the planet is the gray dotted line, and that “r” is the radius of the planet. The tidal force is the difference between the force of gravity on the unit mass M2 at the center of the planet, and the forces of gravity on the unit masses M1 and M3 at the points nearest and furthest from the sun.
Calculating the Tidal Forces
As shown in Figure 1, to calculate the tidal force you can just subtract the gravitational force on the unit mass at the center of the planet from the force on the other unit mass, for example GF1 – GF2. So we can use the equations in Figure 1 to calculate the force.
However, when the distance D is much, much larger than the radius r, we can make some simplifying assumptions. First, we can assume that the force between M1 and M2 is the same as the force between M2 and M3. It’s not, as you can see from the equations … but it is not a large error. For tides from the moon, the individual tidal forces are about ±5% different from their average value.
The next simplifying assumption we can make if D is much larger than r is that the average tidal force can be calculated as
Tidal Force = 2 * G * sunmass * r / D^3
This leads to tiny errors with respect to the sun’s average tidal force on the earth, and slightly larger errors with respect to the moon. For the sun we have
Near side true tidal force on earth (GF1 – GF2) = 0.50590 µN
Far side true force (GF2 – GF3) = 0.50583
True average = 0.50587
Approximation = 0.50587
So the approximation of the average tidal force is good to five significant digits …
And for the moon we have:
Near side true tidal force on earth (GF1 – GF2) = 1.1350 µN
Far side true force (GF2 – GF3) = 1.0796
True average = 1.1073
Approximation = 1.1067
For the moon, the approximation of the average is good to four significant digits. For most results, of course, those differences are far too small to be meaningful, and we can use the approximation without concern.
Why Are There Two Tidal Bulges?
Moving on, let’s look at why there are tidal bulges on both the near and far sides. It’s not because the tidal force acts in different directions, because tidal force is always directed towards the sun. So lets look at Figure 1 again, and this time we’ll include a planet and an ocean. As in Figure 1, the planet is simply free-falling into the sun. That result is shown in Figure 2:
 Figure 2. Tidal forces elongating the planet and the ocean. Note that the planet is elongated as well, but this is not shown in the diagram because obviously, tides in the solid planet are much smaller than tides in the ocean. NOTE THAT THIS PLANET IS NOT THE EARTH.
Figure 2. Tidal forces elongating the planet and the ocean. Note that the planet is elongated as well, but this is not shown in the diagram because obviously, tides in the solid planet are much smaller than tides in the ocean. NOTE THAT THIS PLANET IS NOT THE EARTH.
As the planet free-falls into the sun, the near side of the ocean is pulled the most. So it moves the most, pulling away from the planet. And the planet, in turn is pulled more than the far side, so it pulls away from the ocean. These relative motions create the “bulges”
In other words, the “bulges” on the two sides of the planet are simply a result of the tidal forces stretching the entire system. Indeed, the atmosphere is subject to the same phenomenon, so there are atmospheric tides as well. In prior centuries, these atmospheric tides were said to affect the weather, although in a cyclical rather than a secular manner. However, such connections, while certainly possible, have proven to be elusive and difficult to establish. One complicating factor is that the atmospheric tides that are caused by the sun occur in combinations with solar heating, which makes the atmosphere swell. Also, the variations in pressure caused by the atmospheric tides are small, on the order of a tenth of a millibar (or of a hectopascal), or a variation of only 0.01% …
Finally, I’ve said that the situation in Figure 2 shows that planet free-falling into the sun. As it gets closer and closer, the tidal forces stretching the system get greater and greater, stretching the system more and more. Eventually, at a distance called the “Roche limit”, the tidal forces can reach such strength that they rip the planet into pieces … dang, to have a ring-side seat right on the Roche limit line for that spectacle would be awesome, even if it were perhaps a bit warm …
My best to all,
w.
PS—As with gravity, every mass in the universe exerts a tidal force on every other mass, so you can personally take credit for raising a tide on the surface of the sun … yeah, it’s a small tide, but it’s real. Just sayin’, I had someone claim the opposite. Lots of tidal misinformation out there.
THE USUAL: If you disagree with me or anyone, please quote exactly what it is you disagree with, and tell us precisely why you disagree. That way, we can understand exactly what it is you object to.
millinewton (mN, or 10-6 newtons
1-^(-3) newton. ‘Milli’ means 1/1000 th
Thanks, Leif, fixed. It’s micronewtons …
w.
Figure 2 and it’s accompanying explanation seem to imply that the major axis of the simplified ellipse of the ocean (in cross section), is always pointed towards the sun. But the major axis (of the simplified cross sectional view of the oceans) should surely be oriented towards the moon, which is why the tides change from day to day.
Those Greek letters can be a real pain! Teachers may have a question with micro newtons, but micro is represented by the Greek letter mu, however if the symbol font is not available, then mu becomes m and the answer is off by a factor of 1000 and students get confused.
Willis, I learn something from each of your posts.
Thank you!
Willis, not sure about your numbers but also you seem to be calculating a force per unit mass (N/kg) and not a force in newtons. The tidal force (per unit mass) formula should also have D-cubed and not D-squared.
Nicely done Willis, a very clear explanation. Thank you.
Werner – alt+230 = mu = µ
I also like alt+0176 = °, alt+0153 = ™, alt+0177 = ± alt+0174 = ®
Possible typo, I believe the farthest unit mass is M3.
[Thanks, fixed. -w]
For me the math is not fine with paper, pen, calculator…..but entering on the compute really sucks. Thanks Willis.
William Sears says:
February 14, 2014 at 7:06 pm
I think the units are correct. Consider gravitational force. The units of G are N m2 / kg2.
As a result, G * m1 * m2 /D^2 (gravitational force) has units of
G ( N m2 / kg2) * m1 (kg) * m2 (kg) / D^2 (m2)
The kg and the meters cancel out leaving newtons for the unit of gravitational force. Since tidal forces are the difference of graviational forces, they also are measured in newtons.
Thanks, typo, fixed.
w.
With 3 bodies in play here, (earth, moon, and sun), are there not more than two bulges on opposite sides of the earth? In other words, if the earth was an all-water sphere with no land, what would be the length of the radius as measured from the earth’s center to the surface of the water as a function of its angles in a spherical coordinate system? With no continents to set any boundaries, it seems to me that it would be possible for more than one mode of a standing wave (bulge).
matthew says:
February 14, 2014 at 6:57 pm
Thanks, Matthew. Remember that this is a simplified situation, with a planet free-falling into the sun. There is no moon in this simplified setup, just the sun and the planet.
w.
Willis,
I must admit that I have never given much thought about the tides. I knew the sun was a factor and thought the moon was the other important factor but never really thought much deeper.
From your explanation, could the bulge opposite the sun be explained as a resultant force created by the centripetal force resulting from the earth’s orbit around the sun?
You’ve got me thinking and now I can’t rest until I fully understand the tides. Ohh, that need to know thingy.
Yes Willis, this would be true except for the fact that you do not have an m1 and an m2 in your formulae. You have only the sunmass with no earthmass. Also the numbers that you have calculated appear to have used only one mass, that of the sun.
Willis,
Also in your figure 1 caption you say “Solar tidal forces on a 1-kg mass at the earth’s surface average about half a micronewton (µN, or 10-6 newtons)” which means that you actually agree with me and were just a little sloppy elsewhere. Although I don’t think this is quite the right way of saying this as the tidal force that you have calculated is applied over the radius of the earth (per unit mass) and is not the force on a kilogram mass laying on its surface, tidal or otherwise. I’m in a pedantic mood this evening but will soon fall asleep. I think that I’m in a later time zone than you are.
OK Willis, now my computer has refreshed after making the above comment and I see what you are expressing in a free falling earth. But even if outside the scope of your discussion, for my need to know, in reality would the bulge opposite the sun be from centripal force?
Willis,
Love reading your stuff.
Ever about the tides and if they could induce some kind of spherical harmonics within the ocean?
http://en.wikipedia.org/wiki/File:Spherical_harmonics.png
Thanks for presenting a clear explanation of tidal forces and thus why there is a tidal bulge on the backside of the Earth for both the Sun and the Moon, Willis.
I would like to add 2 points:
1. Atmospheric contraction and expansion contribute to its tidal bulges, but not so for the oceans. Sea tides rise and fall solely due to the lateral flow of sea water.
2. While the tidal bulge on the “backside” of the Earth is due to the Earth being pulled toward the Sun and the Moon, and NOT due to any force directly acting on the seas, to an observer it appears as though the waters are flowing away from the Sun and the Moon. It is the same type of effect that makes the Sun appear to rise or set when it is actually the horizon that is moving. Just as it is normal to speak of the Sun rising, it is normal to speak of the seas flowing towards the backside bulge.
SR
Thanks Willis, very good explanation, but I think this one is also very clear:
Ocean Tides:
The tides that we see in the oceans are due to the pull of the Moon and the Sun. The simplest explanation is that the water on the side of the Earth closest to the Moon is pulled, by the Moon’s gravitational force, more strongly than is the bulk of the Earth, whereas the water on the side furthest from the Moon is pulled less strongly than the Earth. The effect is to make bulges in the water on opposite sides of the Earth. The effect of the Sun’s pull is similar, and the tides that we see are the net effect of both pulls.
When the pull from the Sun adds to that of the Moon, the tides are large and we call them Spring tides, whereas when the pulls are at 90 degrees, the tides are small and we call them Neap tides. The heights of spring tides are governed by the distance of the Moon from the Earth, being largest at Perigee (when the Moon is closest to the Earth) and smallest at Apogee (when the Moon is at its furthest).
Because the Sun’s pull is aligned with that of the Moon at New Moon and Full Moon, these are the times when Spring Tides occur. The pull of the Sun is less than half that of the Moon, and so the frequency of the tides is determined by the apparent passage of the Moon around the Earth, which takes just over a day. We, therefore, in most places on the Earth have two tides a day, with the time of each becoming later from one day to the next by just under an hour a day. (The actual period is, of course, determined by the rotation of the Earth and the orbit of the Moon).
Produced by the Information Services Department of the Royal Greenwich Observatory (1996).
From http://www.oarval.org/tides.htm
Problems
One the earth is not falling into the sun it is semi steady in orbit around it.
Therefore the gravity would be attracting each piece of the earth and sea at the right amount to keep it rotating around the sun. Hence nothing should be moving in respect to anything else.
Imagine 4 balls going around in orbit next to each other. There is no reason for them to move out of their orbits relative to each other.
Hence how do tides form?
Know I am wrong but look forward to explanation .
Second the moon is actually the greater attractor than the sun by a small percentage (WIki) and both together give king tides and both apart 45 degrees give neap (low) tides.
Not that this detracts from your explanation of tides, just rounding out the edges.
Third is the rotation of the earth important in tide formation, not mentioned here.
Angech,
Consider that the four balls are next to each other but at different distances from the sun. They will have different orbital periods and thus will separate from their initial alignment. Connect them with a string as in Willis’ analogy and a tensile force is required to keep the alignment. This is the tidal force. The rotating earth will have an effect both because of the centrifugal and Coriolis forces of a non-inertial frame and the rotation of the tidal bulge. Willis has discussed the latter elsewhere.
For a great explanation of the tides as caused by the moon on Earth watch the series The Mechanical Universe And Beyond. It is a physics course created at Cal Tech for high school or introductory physics. Look at Program 25 Kepler to Einstein. http://www.learner.org/resources/series42.html#
Great explanation and computer graphics illustrating what they are talking about. This whole series is really worth watching. It is available in the US and Canada through Annenberg Learner, I think it’s on Youtube as well.
in reality would the bulge opposite the sun be from centripal force?
++++++++++++++++++++==
Nope.
Before I get called on it I should have said centrifugal force instead of centripetal in my comments above.
Long day, time for bed. 🙂
Before I get called on it I should have said centrifugal force instead of centripetal in my comments above.
========
Nope.
Its circular motion not apparent forces and inertia
Richard D says:
February 14, 2014 at 9:47 pm
Not so, Richard. In the example shown in Figure 2, there is no circular motion, and inertia is not an issue.
w.
Willis Eschenbach says: Not so, Richard. In the example shown in Figure 2, there is no circular motion, and inertia is not an issue.
++++++++++++++++++
You’re right re:figure 2, thanks……. I was looking at centripetal/centrifugal which got me off tract.
As with gravity, every mass in the universe exerts a tidal force on every other mass, so you can personally take credit for raising a tide on the surface of the sun … yeah, it’s a small tide, but it’s real.
+++++++++++++++++++++++++
Thanks for that Willis. Takes me back to the physics classroom.
Problems
One the earth is not falling into the sun it is semi steady in orbit around it.
Therefore the gravity would be attracting each piece of the earth and sea at the right amount to keep it rotating around the sun. Hence nothing should be moving in respect to anything else.
Imagine 4 balls going around in orbit next to each other. There is no reason for them to move out of their orbits relative to each other.
Hence how do tides form?
Know I am wrong but look forward to explanation .
———————————————————————————————————–
So, this will be hard to explain without drawing a diagram, but….
For simplicity, consider a two body system, with a fixed, Sol-centered reference frame and Earth as a moving body, however not yet in an orbit about Sol. As the Earth passes, the mutual gravitational attraction of Sol and Earth modifies the trajectory of Earth, which we call gravitational force. The gravitational force is equal to the change in momentum of earth with respect to time (F = dp/dt = d(mv)/dt = v*(dm/dt) + m*(dv/dt)). We assume both Sol and Earth are fixed mass, reducing the first term to zero and recognize dv/dt to be acceleration. Thus, the gravitational force is F = ma. Because of how the gravitational force equation is defined, the induced acceleration on Earth is towards Sol (the sign convention used in the derivations skipped in this and above). From this definition, you can see that Earth “falls” towards Sol, in the same way that an object dropped from a height “falls” to the ground.
You must remember the fact that momentum, velocity, and acceleration are all vectors. Even in a constant elliptical orbit, Earth will always be accelerating towards Sol. Were you to remove Sol (and, therefore, the force of gravity), Earth’s inertia will carry Earth along the same vector it was traveling at the moment of the disappearance of Sol. The continuing presence of the gravity force continuously accelerates the velocity of Earth about Sol. Even in a truly circular orbit (i.e. radial velocity is constant; rectilinear velocity magnitude is constant), the rectilinear velocity must be constantly accelerated to maintain the orbit. This is done by “pulling” Earth towards Sol. This is why we say it is constantly falling.
Now, for all of that, we traditionally think in terms of point masses, because it’s easier to think about (remember the physics student joke: a horse is a sphere, if it makes the equations easier). In reality, we should treat every body as a continuum of mass elements.
Properly speaking, Willis’s diagram would have a near infinity of mass elements, each working a different amount on each other, with a bunch of other interactions drawn on there. For ease, though, let’s leave the “solid” Earth as a single body. This is an easy idealization to do, since we assume that the frictional forces between the elements are such that they overcome the gravitational force differential between the elements and that the Earth is incompressible. Thus, we assume that the solids would move as one (i.e. the definition of a solid being that it holds its shape and volume in any container). In fact, there is a certain amount of deformation that takes place, as with all solids, in something called “creep”, but we deem this negligible and cancelled out by the rotation (think of it as a rotisserie chicken; we cook it evenly on all sides, so we neglect the temporal differences).
The fluid portions, however, do not have the same amount of friction between them, and therefore “slosh” more easily. The friction between the elements is insufficient to overcome the differential. As a bulk, it will still “fall” about the same as the solid Earth towards Sol (consider the magnitudes of each value input). The different individual elements, however, have are just different enough for us to perceive it.
In truth a fully solid Earth has the same “tidal force” as our blue and green Earth. It just manifests differently, due to the internal forces. The atmosphere “sloshes” far more than the oceans, but it doesn’t really matter to us (the pressure difference being small due to the low densities involved). Were the oceans made of molasses, the same tidal force would again be generated, but the oceans would deform far less (more viscosity = more internal friction to resist deformation).
I hope that helps a bit.
Still is the tide calculation based on Laplace’s tidal equations which states:
from http://en.wikipedia.org/wiki/Tide
“Ocean depths are much smaller than their horizontal extent. Thus, the response to tidal forcing can be modelled using the Laplace tidal equations which incorporate the following features:
1 The vertical (or radial) velocity is negligible, and there is no vertical shear—this is a sheet flow. 2 The forcing is only horizontal (tangential).
3 The Coriolis effect appears as an inertial force (fictitious) acting laterally to the direction of flow and proportional to velocity.
4 The surface height’s rate of change is proportional to the negative divergence of velocity multiplied by the depth. As the horizontal velocity stretches or compresses the ocean as a sheet, the volume thins or thickens, respectively.”
I repeat: The forcing is only horizontal (tangential).
More here:
http://en.wikipedia.org/wiki/Theory_of_tides
“One complicating factor is that the atmospheric tides that are caused by the sun occur in combinations with solar heating, which makes the atmosphere swell. Also, the variations in pressure caused by the atmospheric tides are small, on the order of a tenth of a millibar (or of a hectopascal), or a variation of only 0.01% …”
I fear there may be a misconception here, or perhaps 2. Take a column of air, or water, and measure the pressure at the bottom. Now heat the air, or the water, so it expands upwards. Unless any can leak out sideways the same mass of air or water is till there in the column so the pressure at the bottom must be constant. So whether the atmosphere swells or not, the pressure remains constant.
Now for atmospheric tides. As the earth rotates so the bulge of water tries to remain directly on the line connecting the centre of the earth to the attractor. But friction, inertia, and the continents prevent this happening. So water piles up on the edges, and we see the phenomenon of tides. The atmospheric bulge also tries to stay in the same place, but still there is friction, and hills and mountains get in the way. So the effect of the atmospheric tide is amplified in some places and is minimized in others. I believe it true to say that were the earth a perfect sphere, with a uniform layer of water, the actual rise and fall of the sea level due to tides would be as little as a foot (the surface of the solid earth is also reputed to distort about a foot as well). As all well know, in certain places the tidal effect is greatly magnified, eg, Bay of Fundy with tides up to 40 ft. Just so with the atmospheric tide, and a barograph will record the daily rise and fall of air pressure of up to 3 mb in particular locations. So while the theoretical variation in pressure doe to the atmospheric tide may be 0.1 mb, the observed variation can be 20 or 30 times as great.
The tidal force is affecting every part of the planet.
The force that actually move fluid as water and air is according to Laplace the horizontal (tangential) force.
The vertical force can not move the fluid.
The result of the tangential force is the bulges. It is not the vertical force that create the bulges since water does not expand.
The reason the vertical force are at maximum at bulge maximum is causing the common misinterpretation that the vertical force is the reason for the bulges,
The horisontal forcing is the reason why the earth rotation and tilt and moon inclination have an impact on the direction of tidal induced movement of earths fluids.
Moon inclination is 5.145° to the ecliptic which is between 18.29° and 28.58° to Earth’s equator.
That is then also the direction of the tidal induced fluid movement direction. Fluid is our ocean water and atmosphere are depending on how high the moon are above (or below) the horizon in mornings and evenings when vertical tidal force are at maximum.
Same for solar tide.
Quite a nice explanation Willis. Since there is a huge amount of confusion about this subject, it’s good to have this over-view.
However, one thing is inconsistent in your description.
“There are two different tidal forces of interest in the diagram, which are GF1 – GF2, and GF2 – GF3. ”
That is correct and you will see that are roughly equal and of opposite sign.
” It’s not because the tidal force acts in different directions, because tidal force is always directed towards the sun.”
There you are confusing the tidal raising force (a difference) which you had correctly explained up to that point and the gravitational attraction which is indeed in the same direction, just slightly different in magnitude.
Your piece of blue string is of course the earth’s own gravitational field that is many orders larger than the tiny tidal forces. That’s why tides are only a few metres on a planet thousand of kilometres across.
“string” is not a particularly good idea, a strong steel cable may be better. The cable would hold M1 and M3 anchored in place, but would stretch a little, allowing the ‘tides’ to rise.
So as the proud author of the gem you opened the article with, I note your explanation is in agreement with what I wrote, if you don’t confuse tidal force, the difference in gravitational attraction with gravitational attraction itself.
“The tide raising force acts in both directions (bulge on each side in the simplistic model)”
( GF1 – GF2 ) is negative ( GF2 – GF3. ) is positive. They are roughly equal in size.
Otherwise this nice and clear and easily digestible to a more general readership. Nice work.
Here is my attempt at presenting it. It’s somewhat more technical in language
http://climategrog.wordpress.com/?attachment_id=776
Clive Best has also written a good description with some fairly detailed equations rather then just considering the straight line forces along the earth-moon axis.
http://clivebest.com/blog/
( GF1 – GF2 ) is negative ( GF2 – GF3. ) is positive.
No, that badly put. The point is M3 is accelerated faster towards the sun , faster than the solid earth , M1 less fast than the solid earth. So _when viewed from the point of view of the solid earth_ the forces act in opposite directions.
“I think the units are correct. Consider gravitational force. The units of G are N m2 / kg2.
As a result, G * m1 * m2 /D^2 (gravitational force) has units of
G ( N m2 / kg2) * m1 (kg) * m2 (kg) / D^2 (m2)
The kg and the meters cancel out leaving newtons for the unit of gravitational force. Since tidal forces are the difference of graviational forces, they also are measured in newtons.”
Yes Willis but drop your logic and just look at your tidal force equation that need to be explained:
Tidal Force (N/kg) = 2 * G ( N m2 / kg2) * sunmass (kg) * r (m) / D^3 (m3)
Cancel away. m2 is cancelled by the m/m3 and only one of the kg’s cancel.
Are the units not N/kg?
Two other commenters above seem to have come up with this answer.
You are familiar with these tidal force equations and not myself, yet, so maybe you can explain the discrepancy in either your logic or the tidal force equation itself.
This is all about what scientists refer to as “frame of reference” , it depends up on where you’re sitting as to how you view things.
Willis adopts a frame of reference outside the earth which is rotation about the sun but he does not discuss the centrifugal and Coriolis “fictitious forces” that are necessary if you do that. The other way is regard it as an instantaneous snapshot of a system in rotation where gravity provides the centripetal force that causes the roughly circular orbital motion.
That is the approach I adopted because you can avoid the complication of fictitious forces.
http://climategrog.wordpress.com/?attachment_id=776
Sorry folks, but bits of string and billiard ball mechanics don’t work correctly if the billiard table is on a rotating platform. All this “frame of reference” stuff is not a simple idea but you can’t just stop the earth going round the and forget about it.
I like the simplicity of Wilis’ diagram but he needs to add the centrifugal “fictitious force” acting outwards (to the left). When you do that you find the net force on M1 is to the left and the net force on M3 is to the sun . We then see the equivalence with my statement about opposite forces.
Wayne.Your analysis is correct.
Tidal Force (N/kg) = 2 * G ( N m2 / kg2) * sunmass (kg) * r (m) / D^3 (m3)
“Are the units not N/kg?”
Well, no. It’s because Willis had written his equations for a unit mass of 1kg. and thus left out one of the m’s
The force should be of the form GmM/d^2 , he leaves out the m which is 1kg. It would be clearer to leave it in.
Music for physicists, outside of my benchtop chemistry and lately jewelry comfort zone. Thanks to Willis, WUWT is becoming Khan Acadamy, an online college, so here I can at least at times study my old man eyes out, as an empiricist, delving into new ways to prove those rat bastard theorists of Nature wrong again. Sometimes correctly.
I still think there’s a better groking of Maxwell’s equations out there somewhere in rebel controlled space.
Willis? Torqued space? Wither the aether?
Lubos won’t go there. He’s not a classicist, even in spirit, ever.
The three body problem alone, but add to it the severe inability of overheated supercomputers to even fold simple Tinkertoy proteins right, the stuff of life, and theory becomes just an adjunct to real lab work. Benchtop chemists always bust limits, lately the diffraction limit of traditional optical microscopes.
Oh, they’ll catch up, dragged kicking and screaming, into Reality.
Willis,
I usually enjoy reading your articles because I think you have a gift for explaining complex matters in a correct and simple way, but unfortunately I think this is an exception.
You say:
From this one could think that the distance between the Sun and the Earth is decreasing, but that is not the case, it is increasing.
The tidal force interacts with the rotation of the Sun and causes the Earth to be pushed slightly outwards every year. The energy for the push is taken from the Sun’s rotational energy.
We have the same effect between the Earth and the Moon. The earth is rotating slower and is pushing the moon away.
See:
Sun – Earth distance increasing one micrometer per year:
http://curious.astro.cornell.edu/question.php?number=317
Earth – Moon distance increasing 3 cm per year
http://www.newton.dep.anl.gov/askasci/ast99/ast99639.htm
/ Jan
Angech ponders the tides.
There is a minute change in the value of g which leads to a minute bulge .
The g value is the gravity of the moon not the sun.
It is actually twice as strong as the gravity of the sun on the earth tides as it is much closer to the earth.
The moons gravity is a lot weaker than the earth’s so any effect on bulges (tides) is a lot less than I originally contemplated and the effect of the sun is even less!
Why are the tides longer than 12 hours
The moon orbits the earth every 28 days so the tides are 24 hours divided by 28 means about 50 minutes later every day.
Are their minor tides due to the effect of the sun alone separate to the main 2 we realise.
Once actual movement occurs rotational effects and shallowness of sea beds and Coriolanus forces may make the waves much bigger
Willis
Hi
not strictly on topic but I saw an interesting post on Bishop Hill by a commenter called Paul K which I set out below. The connection to your piece is the gravitational effect on the ‘solid earth’.
Regards
“Personally, I think that it wouldn’t do to underestimate the importance of the England paper – even if it is founded on poor data.
As Nic correctly points out, from the observed data, the total global ocean heat flux shows a peak around 2001-2005 depending on which dataset one takes. TOA radiative measurements show a peak in net radiative incoming flux somewhere around 1997-2000, driven largely by SW changes in net albedo. Modern MSL data from satellite altimetry (or indeed from tide gauge data) shows a peak in its derivative function around 2001-2003, which should also be a proxy for net heat flux going into the ocean. (Using gravimetric data from GRACE, we can rule out the possibility that the peak in MSL derivative was caused by mass addition – it is a peak clearly driven by thermosteric expansion. There is a useful presentation here by Nerem: http://conference2011.wcrp-climate.org/orals/B3/Nerem_B3.pdf) So there is a consistent story from three data sources which says that the net incoming flux hit a peak and has since been decreasing overall for about a decade. This is not compatible with increasing forcing from GHGs and flat or declining tropospheric temperature – a mini paradox, if you will.
The mini-paradox becomes a major paradox when we consider the historical behavior of MSL from tide-guage data. The derivative function of the MSL data shows a dominant and remarkably consistent quasi-60 year cycle. It shows dominant peaks around 1750, 1810, 1870’s and 1940s. (See Jevrejeva 2008.) In other words, the modern peak in the MSL data came in right on time relative to previous recorded oscillatory cycles which date back to 1700. Using the modern peak for calibration, which we know relates to a peak in incoming net flux, we can very reasonably infer that the previous peaks were also due to peaks in net heat flux. The paradox is that these dates for peak incoming flux correspond closely to peaks in the multidecadal oscillations of surface temperature. This is a major bust. This is exactly pi radians out of phase with what we would expect if these cycles were caused by an unforced redistribution of internal heat. (High surface temperatures should induce an increase in outgoing radiation which translates into a decrease in net incoming radiation.) I think that we are therefore led to the inevitable conclusion that these are forced climate oscillations, which means that we have to look for a new flux forcing to explain them, since the current selection box does not have any forcings of the correct frequencies. I now return to the work of Matthew England. His work adds an important piece to the jigsaw puzzle, even if he himself is failing to appreciate the implications. We saw from Kosaka and Xie 2013 that a large chunk of the late 20th century heating as well as the modern temperature hiatus could be captured by the simple expedient of prescribing sea surface temperatures in a small area of the eastern Pacific. Those temperatures are in reality controlled by ENSO events which are in turn controlled by equatorial trade wind strength and direction. England’s work confirms at least in skeletal form that controlling the wind stress tensor in the same area gives a similar result, even if he is wrong on some of the details.
The question it leaves is: what then controls the equatorial trade winds? The answer was actually known more than 40 years ago when science was still relatively unsullied, but it will not be accepted easily by mainstream climate science today, since the answer makes not one but two major breaches in fundamental assumptions of climate science.
The first part of the answer is that the climate oscillations are triggered by gravitationally forced changes in the angular velocity of the solid Earth. These changes transmit a (non-radiative) momentum flux into the hydrosphere and atmosphere via frictional torque and conservation of angular momentum. These changes explain the fluctuations in trade winds and, just as importantly, the latitudinal meanderings of the jet streams. Before anyone starts calling for the men in white coats, I would suggest that you have a look at this 1976 paper: http://gji.oxfordjournals.org/content/46/3/555.full.pdf and this: http://gji.oxfordjournals.org/content/64/1/67.full.pdf . For the excellent correlation apparent in the higher frequency data between Earth’s rotation velocity, atmospheric angular momentum and ENSO events, you might also try this paper: http://trs-new.jpl.nasa.gov/dspace/bitstream/2014/17186/1/99-0613.pdf .
So it seems that England has probably confirmed that the multidecadal oscillations are driven by atmospheric tides which are driven by a non-radiative orbital forcing. He just hasn’t realised yet that what he has done is to demonstrate that the GCMs are all missing a massively important piece of physics which was considered small enough to be neglected on energetic grounds. The story doesn’t end there. The orbital forcing is a triggering and control mechanism, but it is “energetically deficient” to explain the full amplitude of the climate oscillations. On my sums the trough-to-peak transfer of energy via momentum flux and friction amounts to something less than 2*10^22 joules during the 60-year cycles. The amplification factor comes from the cloud response to the change in phase of the orbital forcing, which is why we note the dominant effect of SW changes in the radiative signature. This is a feedback mechanism of sorts, but it is not a “temperature dependent” feedback mechanism; it does not correlate simply with global surface temperature, but rather with the phase of orbital forcing. This post is already too long for me to try to explain how that works. I am hoping if I live long enough to try to get some of this stuff down in more detail in an article for Lucia, but I do keep getting distracted, not to mention beaten up by my wife for wasting time on that climate change rubbish instead of doing something useful.
Feb 14, 2014 at 2:35 PM | Paul_K”
Let’s test this theory. How does one go about measuring the “tidal force”?
The logical consequences of the tidal theory (such as elongation and Roche limit) have been falsified by observations. Metis and Pan orbit inside the Roche limit. Pan seems to be accreting. Far from being elongated, the Moon has a deficit of material on the near side.
http://burro.cwru.edu/Academics/Astr221/SolarSys/lunaint.gif
Other than that, can any 2- or 3-body theory (plus rope) explain the real ocean tide? As understand, tide prediction is not physical. It uses harmonic curve-fitting.
http://web.vims.edu/physical/research/TCTutorial/tidepredict.htm
The idea that there are two bulges on the planet is also too ideal. It is true that there are places where one sees the passage of two maxima every day, but that does not mean there are two bulges on the planet.
I would love to see a similar animation with the position of the Moon plotted on it.
For some reason my instinct says that this explanation cannot be completely correct because I ask that if we take away the moon altogether, (leaving only the sun and earth), would there be an ocean tide at all?
If the earth wasn’t rotating then the answer is easily no. If there was any bulge at all it would be very slight, at the same spot and never vary. But earth is rotating and rotating so that the outermost material at midnight is going the fastest above earth’s center’s orbital velocity resulting in it bulging outward away from the sun and the material at noon time going the slowest below earth’s center’s orbital velocity resulting in it bulging toward the sun thus resulting in a double bulge – without any moon at all.
Is this rotational factor significant? I’ll have run the numbers or wait for someone else to do it.
I really meant, instead of “If the earth wasn’t rotating”, – – “If earth rotated once per year”
Fascinating, Willis.
Isn’t it amazing how such things are often (always?) more complex than they seem at first glance.
No wonder the “Post-Normal” science lot suffer from physics envy.
A quick look gave me a result for a “no moon” variation of “midnight fling” acceleration over average center V^2/R of 3%. For now I’d say it looks significant.
Earth’s average orbit velocity V1 as 29885 m/sec. Crust WRT center V2 as 463 m/sec. So combined velocity in orbit around the sun at midnight V1+V2=V3 as 30349 m/sec V3^2 / V1^2 = 1.03
More on the Roche limit.
Images for the Roche limit
NASA on the Roche limit: Tidal Forces: Let ‘er Rip
Greg says:
February 15, 2014 at 1:55 am
Not true at all. I have a heliocentric (sun centered) frame of reference, which does NOT rotate about the sun. Neither does the planet in my example. The clue is where I say it is free-falling into the sun …
w.
Boiling it down, I’ve produced a two bulge tide model with no moon at all. Earth to Sun acceleration due to gravity is .006 M/sec^2 Plus 3% at midnight, minus 3% at noon makes it a change plus or minus .0002 m/sec^2 against our earth gravity of 10M/sec^2
Certainly tiny WRT to earth’s gravity at sea level but how much does that contribute to the formation of two lobes?
Willis, could you show the combined tidal forces on Earth from the Sun and Moon for both new and full moon positions.
Greg says:
February 15, 2014 at 1:33 am
Yeah, right … do the math again, Greg. Then do it again, again. At some point in there you might notice that they are roughly equal, but that they have the same sign.
I didn’t want to point out that you were the fool in the head post who made the same incorrect claim that the two forces acted in different directions. Instead, I said that perhaps you understood the tidal forces, but your words were just confusing … but now that you’ve restated your idiocy, I see you actually don’t understand.
DO THE FREAKING MATH, Greg. The two have the same sign.
This, of course, is as we’d expect. From the sun’s point of view, there is nothing to distinguish the first pair of masses (M1 & M2) from the second pair of masses (M2 and M3). So why would one be pulled in one direction by the tidal force, and the other be pulled in the other direction?
Math is your friend …
w.
In other words I’m stating that, simply by virtue of earth’s rotation, everything on the surface of earth weighs .002% less at midnight and noon than it does at 6am and 6pm.
wayne says:
February 15, 2014 at 1:53 am
I guess you missed the part where I said that GF1, GF2, and GF3 were the forces on a 1 kilogram mass. Obviously, if it were a two kilogram mass, the force would be twice that.
That is to say, the left half of your equations should be newtons times kilogrammes, not N/kg … I figured that most folks would understand that. However, it appears I underestimated you.
w.
Mike M says:
February 15, 2014 at 8:12 am
In other words I’m stating that, simply by virtue of earth’s rotation, everything on the surface of earth weighs .002% less at midnight and noon than it does at 6am and 6pm.
When is it noon at the North Pole?
Jan Kjetil Andersen says:
February 15, 2014 at 3:05 am
Jan (and others), the planet shown free-falling into the sun IS NOT THE EARTH. Here’s a clue to tell them apart … the planet in Figure 2 is free-falling into the sun. The earth is not.
As a result, although it is assuredly true, in this makes no sense to say “the distance between the sun and the earth is increasing” … we’re talking about planet free-falling into the sun, not the earth.
w.
Willis you say : “… because tidal force is always directed towards the sun.”
That sentence end could use a little correction/clarification I think.
Mike
A slight digression. Canute is mentioned in the title. May I put a word in for this king. When he said that he was commanding the tides he was not doing this out of hubris but to show his people that he had his limitations. Now there is degree of modesty that some warmists could benefit from.
lsvalgaard says: When is it noon at the North Pole?
Maximum kinetically induced differential is obviously at the equator so times the cosine of the latitude.
By all due respect, this is a rather misleading statement
The planet does not “fall into the Sun”. The gravitational pull is countered by the centripetal acceleration of the Earth in its orbit around the Sun.
The centripetal acceleration is the phenomenon one can feel in a carousel. One can feel an outward force away from the center of the spinning point.
The centripetal acceleration is given by the formula:
The planet stay in the orbit because the centripetal acceleration, a, is equal to the gravitational pull from the Sun
But as we see from the formula, a increases with the distance from the Sun. On the other hand, the gravitational pull from the Sun decreases with the distance from the Sun.
The centripetal acceleration is therefore greater than the gravitational pull in point M3 and weaker than the gravitational pull in point A1. In point A2 they are equal.
This means that the greater “carousel force” felt by the centripetal acceleration in M3 combined with the less gravitational pull, makes the oceans bulge out and away from the Sun.
In M1 we have the opposite situation. The smaller carousel effect and larger gravitational pull from the Sun makes the oceans bulge out from the Earth, but toward to the Sun.
/Jan
Mike M says:
February 15, 2014 at 8:35 am
Maximum kinetically induced differential is obviously at the equator so times the cosine of the latitude.
everything on the surface of earth …
And you statement is not correct anyway, as the rotation of the Earth causes things to weigh less at all times at the equator.
lsvalgaard says: “everything on the surface of earth …”
Okay, you got me, everything BUT an infinitesimal sized point at each pole – happy?
“And you statement is not correct anyway, as the rotation of the Earth causes things to weigh less at all times at the equator.”
That’s a CONSTANT, (also per cosine of latitude)… I’m looking at variations in acceleration.
Jan Kjetil Andersen says:
February 15, 2014 at 8:37 am
By all due respect, this is a rather misleading statement
The planet does not “fall into the Sun”. The gravitational pull is countered by the centripetal acceleration of the Earth in its orbit around the Sun.
Amazing how many experts we have around here. Willis is completely correct [apart from a few typos in the beginning]. This tidal effect has nothing to do with rotation, centripetal forces, orbital movement or any of that.
Mike M says:
February 15, 2014 at 8:44 am
I’m looking at variations in acceleration.
Variations caused by what?
Willis, the idea that a person free falling into a black hole feet or head first will be at some point ripped apart lengthwise is a common one and consistent with your assertion.
“DO THE FREAKING MATH, Greg. The two have the same sign. ”
How about reading where I corrected that statement ???
“Not true at all. I have a heliocentric (sun centered) frame of reference, which does NOT rotate about the sun. Neither does the planet in my example. The clue is where I say it is free-falling into the sun …”
OK, I didn’t realise you intended not to rotate anything. So you want to call be a fool for saying something about how planets moons and tides work by comparing to a situation where nothing rotates.
Should still be an interesting exercise.
It’s not clear what the mechanical properiteis of your piece of “string” are so I’ll stick with a steel cable.
As I think we are agreed GF1>GF2>GF3 so the outer mass would accelerate less and get left behind unless it was tethered. Inversely M1 would fall faster. So both cables are under (rougly equal) tension.
You show that we can ignore the asymmetry:
True average = 0.50587
Approximation = 0.50587
So the net force accelerating the three masses is 3GF2 acting 3kg, They experience a common acceleration (since they are tethered) equal to that of the centre mass alone.
But M3 is experiencing less gravitational attraction and has to be pulled by the tether to the tune of GF2-GF3. The tension in the tether is thus that value. Similary the other side which should accelerate more but is held back by the tether.
So at M2 the tensions in the tethers are equal and in opposite directions.
The cables will extent a little due to the tension and both masses will end up a little further away from M2 and continute accelerating as an ensemble. This is the equivalent of the two tideal bugles. The tidal force and the ‘tide’ (stretch in cable) will remain constant until they get significantly closer to the sun and the gravity gradient gets steeper.
All you have done is substituted free-fall acceleration to the sun , without rotation, for a centripetal acceleration towards the sun with rotation.
The difference terms remain the same and act in opposite directions. If they didn’t one of the cables would be lack.
Even a “fool” like me can see that.
slack.
The difference terms remain the same and act in opposite directions. If they didn’t one of the cables would be slack.
lsvalgaard says: “Variations caused by what?”
Read BACK further to my calculations of difference in heliocentric orbital velocity of a point (on the equator) due to earth’s rotation; fastest at midnight, slowest at noon. The kinematic difference compared to the acceleration due to Sun’s gravity, (at earth’s distance), compared to 6am or 6pm, is 3%.
Mike M says:
February 15, 2014 at 8:58 am
Read BACK further to my calculations of difference in heliocentric orbital velocity of a point (on the equator) due to earth’s rotation; fastest at midnight, slowest at noon. The kinematic difference compared to the acceleration due to Sun’s gravity, (at earth’s distance), compared to 6am or 6pm, is 3%.
Not so. The Earth is is free fall and knows nothing about orbital velocity.
So my comments are on moderation now. ?? Is “slack” a moderation tripwise or what?
REPLY: dunno, some triggers are wordpress controlled. May be some spam circulating that uses “slack”…maybe Viagra like – A
lsvalgaard says: Not so. The Earth is is free fall and knows nothing about orbital velocity.
I’m done with ya…
Ok, I see
I thought it was something totally wrong here.
I then see that my other comment on misleading description is also misplaced.
/ Jan
Mike M says:
February 15, 2014 at 9:05 am
I’m done with ya…
Good that you stop digging your hole deeper and deeper. According to your ‘theory’ a pendulum clock should vary its ticking rate during the day and it does not.
Just noticed I’d inverted my name to Gerg . LOL, was that what tripped moderation
“DO THE FREAKING MATH, Greg. The two have the same sign. ”
How about reading where I corrected that statement ???
“Not true at all. I have a heliocentric (sun centered) frame of reference, which does NOT rotate about the sun. Neither does the planet in my example. The clue is where I say it is free-falling into the sun …”
OK, I didn’t realise you intended not to rotate anything. So you want to call be a fool for saying something about how planets moons and tides work by comparing to a situation where nothing rotates.
Should still be an interesting exercise.
It’s not clear what the mechanical properiteis of your piece of “string” are so I’ll stick with a steel cable.
As I think we are agreed GF1>GF2>GF3 so the outer mass would accelerate less and get left behind unless it was tethered. Inversely M1 would fall faster. So both cables are under (rougly equal) tension.
You show that we can ignore the asymmetry:
True average = 0.50587
Approximation = 0.50587
So the net force accelerating the three masses is 3GF2 acting 3kg, They experience a common acceleration (since they are tethered) equal to that of the centre mass alone.
But M3 is experiencing less gravitational attraction and has to be pulled by the tether to the tune of GF2-GF3. The tension in the tether is thus that value. Similary the other side which should accelerate more but is held back by the tether.
So at M2 the tensions in the tethers are equal and in opposite directions.
The cables will extent a little due to the tension and both masses will end up a little further away from M2 and continute accelerating as an ensemble. This is the equivalent of the two tideal bugles. The tidal force and the ‘tide’ (stretch in cable) will remain constant until they get significantly closer to the sun and the gravity gradient gets steeper.
All you have done is substituted free-fall acceleration to the sun , without rotation, for a centripetal acceleration towards the sun with rotation.
The difference terms remain the same and act in opposite directions. If they didn’t one of the cables would be lack.
Even a “fool” like me can see that.
The difference terms remain the same and act in opposite directions. If they didn’t one of the cables would be _slack_.
[Mods , you can delete the three posts by “Gerg” 😉 Must have been taken as posting a pseudo form the same email. ]
Willis, I like your rope model, it is very elegant. However, with all due respect, we often formulate dynamical problems from a convenient frame of reference. Pretending that the Earth is an inertial frame of reference is one such convenience. Within this frame of reference the gradient of tide-raising potential appears to act in opposite directions from the center of mass of the Earth-Moon system. The reason for this is the manner in which centrifugal acceleration gets included on the left side of Newton’s equation (The F of F=ma) in the translation from one frame of reference to the other. I don’t see that the view of the matter from this alternative frame of reference is wrong–it does provide correct predictions.
I mean centripetal not centrifugal in my last post.
Kevin Kilty says:
February 15, 2014 at 10:06 am
I mean centripetal not centrifugal in my last post
It doesn’t matter as the tidal effect has nothing to do with rotation or orbital movements.
Willis,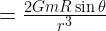
What you write is clear and simple. However the earth is a non-inertial accelerating frame of reference because it is in orbit around the moon-earth barycenter. The mystery of gravity is why the ‘m’ in gravity is the same as the inertial ‘m’ in F=ma. Einstein used this equivalence principal to derive general relativity. The bulge on the opposite side to the moon is not because the centre of the earth feels a stronger gravity than the far side ocean. That only applies to fee falling bodies. It is instead due to the centrifugal acceleration caused by its orbit around the joint barycenter.
The tidal force on the ocean is 10 million times smaller than the earth’s gravity. What moves enormous quantities of water is the tidal component parallel to the surface which is approximately
PS—As with gravity, every mass in the universe exerts a tidal force on every other mass.
No this is not true – An electron does not exert a tidal force on a quark.
lsvalgaard says: “Good that you stop digging your hole deeper and deeper. According to your ‘theory’ a pendulum clock should vary its ticking rate during the day and it does not. ”
Yes, by my theory it does vary! It’s just too small to notice and averages out, cycling every 12 hours. (Like I said, if my numbers are right, the factor is only .002% )
Given that you will not deny that a particle of mass M at the equator is moving faster than earth’s orbital velocity around the sun at midnight and slower than earth’s orbital velocity around the sun at noon – it’s inertial V^2/R reaction (“centrifugal force”) will be greater than its gravitational attraction to the sun (centripetal force) at midnight and less than its gravitational attraction to the sun at noon.
Mike M says:
February 15, 2014 at 11:04 am
Yes, by my theory it does vary! It’s just too small to notice and averages out, cycling every 12 hours. (Like I said, if my numbers are right, the factor is only .002% )
Then your theory is wrong as the orbit around the Sun and around the center of the Milky Way and around the center of the Local Group of Galaxies, and around the… have no measurable effect at all of the weight of ‘everything’ on Earth.
Gravity by far my most favorite subject to read about and ponder. Semi quantified by Newton and refined by my personal hero [Einstein]. The one thing I can take away from the above comments as well as the bulk of my amateur research is that nobody really has a clue. Experimental data results says the math is very close that we currently use to calculate it but the actual mechanism that produces it still eludes us.
For me the simple fact that something so seemingly mundane as a coin falling to the ground is beyond our understanding is captivating. When i contrast this to the state of ” Climate Science ” which does not even get freaking close to meeting model projections makes me laugh and cry at the same time….
lsvalgaard says: “Then your theory is wrong as the orbit around the Sun and around the center of the Milky Way and around the center of the Local Group of Galaxies, and around the… have no measurable effect at all of the weight of ‘everything’ on Earth.”
True or false – They ALL have an affect?
You said I was digging a hole and now look who is crawling into one with “measurable”?
The greatest tidal effect if from the moon. The near bulge on earth is from gravitational force. The far side bulge is created by centripetal force. The moon does not rotate around the earth. They both orbit around a common center of mass which is not the center of the earth.
Mike M says:
February 15, 2014 at 11:25 am
lsvalgaard says: “Then your theory is wrong as the orbit around the Sun and around the center of the Milky Way and around the center of the Local Group of Galaxies, and around the… have no measurable effect at all of the weight of ‘everything’ on Earth.”
True or false – They ALL have an affect?
They have no effect due to rotations or orbital movements. The do have [mostly unmeasurable] tidal effects due to gravity.
FTA: “the author of that statement may understand the tides, but that isn’t how tidal forces work, they don’t act in different directions.”
They do. It’s conceptually a little tricky, but you have made a simple math mistake.
You calculate GF1 – GF2 on the near side. What is this? It is the specific force acting in the direction of the Sun relative to the Earth, i.e., the arrow is starting from the Earth and pointing toward the Sun.
You then calculate GF2 – GF3. This is the specific force acting opposite of the direction of the Sun. The arrow is pointing from the Sun to the Earth.
To get them both in the same direction, you would need to calculate both with respect to the same reference point, GF2.
You see, independently, M1 is experiencing GF1 in the direction of the Sun. M3 is experiencing GF3 with respect to the Sun. With respect to one another, they are experiencing |GF1 – GF3|. This is non-zero, which means the objects are not being pushed in the same direction.
It may help to note that GF2 is actually zero, when you include the centripetal acceleration. Let’s assume we have a circular orbit with angular rate omega = sqrt(mu/D^3). The total specific force acting at the center of the Earth is
GF2 = -mu/D^2 + D*omega^2 = 0
i.e., we are in free fall at the center of the Earth.
The specific force acting on the near side is
GF1 = -mu/(D-r)^2 + (D-r)*omega^2 := (-2*mu/D^3)*r – r*omega^2 = (-3*mu/D^3)*r
The specific force on the far side acting in the direction of the Sun is
GF3 = -mu/(D+r)^2 + (D+r)*omega^2 := (+3*mu/D^3)*r
These specific forces are relative to the Sun. The near one is radially inward toward the Sun, and the far one is radially outward from the Sun. Note that |GF1 – GF3| = (6*mu/D^3)*r, i.e., they are pushing away from each other.
Expat says:
February 15, 2014 at 11:28 am
The greatest tidal effect if from the moon. The near bulge on earth is from gravitational force. The far side bulge is created by centripetal force.
No, very wrong. Both are gravitational. Willis is correct. Rotation and orbital movements have nothing whatsoever to do with the tides.
lsvalgaard says “They have no effect due to rotations or orbital movements.”
FALSE!
Let’s try this again, step by step…
DO YOU DENY that a particle of mass M at the equator is moving faster than earth’s solar orbital velocity around the sun at midnight and slower than earth’s solar orbital velocity around the sun at noon?
“In other words, the “bulges” on the two sides of the Earth are simply a result of the tidal forces stretching the entire system.”
That is a fair desciption. It is the difference in two differenct forces, applied at two different points in the body that exert a tensile stress on the body. You cannot stretch a body with one force. So in the case of two co-linear forces, there will be a net force (the average of the two) actiing to accelerate the body and two opposing components (each half the difference) acting in opposite directions, at the same two points, to stretch the body.
In the case above (GF3+GF1)/2 = GF2 will accelerate each of the three tethered weights at the common rate towards the sun.
Two opposing forces (GF3-GF1)/2 will act at each end mass acting to stretch the tethers applying a tensional stress to the ensemble.
In the case of an orbitting planet, most of the gravitational force is excerted to supply the centrpetal force that produces the centripetal acceleration which ensures the circular orbit. In this experiment it goes to linear acceleration towards the sun.
In both cases there is a residual of two equal and opposing forces that stretch the masses/planat creating the distortions we call “tides”. These are the tide raising forces.
The statement I made yesterday remains valid.
“The tide raising force acts in both directions (bulge on each side in the simplistic model)”
All Willis has done here is to add a large additional force to everything in one direction and then conclude that they all act in the same direction (but with different magnitudes. ). Again, its a question of frame of reference.
It’s a bit like measuring tides as haveing extremes of +/- 2m . Then someone else comes a long , moves the measuring stick and says “no you’re wrong! Here tides are between 8m and 12m , they’re always well above zero”. They then start calling everyone who does not agree with them a “fool”.
Bart says:
February 15, 2014 at 11:34 am
It may help to note that GF2 is actually zero, when you include the centripetal acceleration. Let’s assume we have a circular orbit with angular rate …
Please, Bart. The tidal effects have nothing to do with centripetal accelerations, rotation, orbital movements, etc. Three bodies lined up in the direction of the Sun and falling towards the Sun [[think] of pieces of comet] all are falling under the gravitational force of the Sun directed towards to Sun for all three bodies.
Mike M says:
February 15, 2014 at 11:36 am
DO YOU DENY that a particle of mass M at the equator is moving faster than earth’s solar orbital velocity around the sun at midnight and slower than earth’s solar orbital velocity around the sun at noon?
Whatever you may think of this, such movements have nothing to do with the tidal effects.
lsvalgaard says:
February 15, 2014 at 11:42 am
“The tidal effects have nothing to do with centripetal accelerations…”
Not so. Perhaps you are confusing rotations of the Earth, versus revolution about the Sun. The former has little effect on tides, because it is equally distributed about the Earth. But, the near side of the Earth is indubitably instantaneously accelerating slower with respect to inertial space than the far side.
Bart says:
February 15, 2014 at 11:52 am
But, the near side of the Earth is indubitably instantaneously accelerating slower with respect to inertial space than the far side.
That has nothing to do with the tidal effects. Perhaps the easiest way to see this is that the equations of the tidal heights and for the locations of the Roche Limit make no reference to rotation or orbital movements, only to the dimensions, masses, and distances of the bodies involved.
lsvalgaard says: Whatever you may think of this, such movements have nothing to do with the tidal effects.
Oh, so now you clam up refusing to recognize even a simple statement of relative motion?
I never said it was THE explanation of ocean tides but I stand by my assertion the force differential is REAL and acts to reduce the net gravitational force at the equator at both midnight and noon which would cause a perfect 12 hour tide period if there was no moon present.
The moon injects another component of variation to screw up the timing but then there is the consistence of highest tides occurring at periods of new and full moon which only amplifies my contention.
lsvalgaard says:
February 15, 2014 at 11:57 am
“Perhaps the easiest way to see this is that the equations of the tidal heights and for the locations of the Roche Limit…”
You are wrong. Please do not bother me with any more silly stuff like this.
CliveBert
” The bulge on the opposite side to the moon is not because the centre of the earth feels a stronger gravity than the far side ocean. That only applies to fee falling bodies. It is instead due to the centrifugal acceleration caused by its orbit around the joint barycenter.
The tidal force on the ocean is 10 million times smaller than the earth’s gravity. What moves enormous quantities of water is the tidal component parallel to the surface ”
Yes, I think that is what primarily moves the water volume. However, I think it is gravity that sets a limit on how high it can get. As you say its by far the stronger force.
This is the approach the I took the other day in equating the centripetial force to the local value of gravitational attraction. That provides an instananeous equilibrium level to which it would tend.
http://climategrog.wordpress.com/?attachment_id=776
As we all know , the dynamics is a world away from two (or four) bulges.
Mike M says:
February 15, 2014 at 12:00 pm
I never said it was THE explanation of ocean tides but I stand by my assertion the force differential is REAL and acts to reduce the net gravitational force at the equator at both midnight and noon which would cause a perfect 12 hour tide period if there was no moon present.
A force differential is due to gravity, but is not due to rotation or orbital movement.
Bart says:
February 15, 2014 at 12:01 pm
“Perhaps the easiest way to see this is that the equations of the tidal heights and for the locations of the Roche Limit…”
You are wrong.
The roche limit depends only on the cube root of the ratio of the densities of the bodies [and on the radius of the central body]. As your link says: “we can ignore the centrifugal potential VC and consider only the tidal potential VT”. The centrifugal force being ignored is that of the rotation of a nonspherical body.
Please do not bother me with any more silly stuff like this.
There you go again. A little thought on your part would do you good.
A planet with the dimension and mass as the Earth falling into the Sun from infinity with no centripetal acceleration at all would at the time it distance reached 1 AU experience precisely the same tidal force as the Earth.
Let’s not forget that earth’s crust is extremely thin WRT earth’s diameter and is going to flex to “bulging forces” mostly at the equator along with the ocean. Could that explain why ocean tide varies the least at the equator and greatest at the higher latitudes by virtue that those regions of crust are not being bulged as much making the determination of which way is “downhill” at various times of the day rather complex.. ??
Willis, you *do* have a problem with your signs. You yourself state:
“As shown in Figure 1, to calculate the tidal force you can just subtract the gravitational force on the unit mass at the center of the earth from the force on the other unit mass, for example GF1 – GF2.”
At the other side, your definition would give “GF3 – GF2” (not “G2 – G3”), which is indeed negative. Using the center of mass of the the earth as the frame of reference, the tidal force is away from the center., This is positive toward the moon (as tyou defined your directions), so the far force is indeed negative.
lsvalgaard says:
February 15, 2014 at 12:15 pm
Look farther down. Do you see the equation immediately prior to and following the statement “let us consider how the centrifugal force from rotation will affect the result”? They then add in the centrifugal effects and, as you see, it is the same boost from a factor of 2 to a factor of 3 that I gave in my equations.
Quit making a fool of yourself, Leif. You are wrong. Let it go.
lsvalgaard says “A force differential is due to gravity, but is not due to rotation or orbital movement.”
Oh really, only gravity huh? So if earth’s orbital velocity around the sun slows down it will not fall closer towards the sun and if it speeds up it won’t go further way from the sun? Do you understand orbital mechanics at all?
Tim Folkerts says:
February 15, 2014 at 12:16 pm
Yes, that is me point, before Leif sidetracked me with an irrelevant tangent.
Although we are not talking about earth-moon tidal dynamics, that seems to be shading some of these comments. A review of the detail Noaa Technical Tide description may help…
http://www.co-ops.nos.noaa.gov/restles3.html
Bart says:
February 15, 2014 at 12:18 pm
They then add in the centrifugal effects and, as you see, it is the same boost from a factor of 2 to a factor of 3 that I gave in my equations. Quit making a fool of yourself, Leif. You are wrong. Let it go.
As I said, a little more thought on your part would do you good:
From the link: This is the Roche limit,
d \approx 2{.}423 \cdot R \cdot \sqrt[3]{ \frac {\rho_M} {\rho_m} } \,.
Surprisingly, including the centrifugal potential makes remarkably little difference, though the object becomes a Roche ellipsoid, a general triaxial ellipsoid with all axes having different lengths. The potential becomes a much more complicated function of the axis lengths, requiring elliptic functions. However, the solution proceeds much as in the tidal-only case, and we find
d \approx 2{.}455 \cdot R \cdot \sqrt[3]{ \frac {\rho_M} {\rho_m} } \,.
the change of the numeral factor is from 2.423 to 2.455 thus negligible, and nil for tides on an almost spherical body like the Earth.
Mike M says:
February 15, 2014 at 12:21 pm
Oh really, only gravity huh? So if earth’s orbital velocity around the sun slows down it will not fall closer towards the sun and if it speeds up it won’t go further way from the sun? Do you understand orbital mechanics at all?
The closer the Earth would be to the Sun, the faster it would go, but the orbital speed has nothing to do with the tides.
The equivalence principal is the fundamental assumption of general relativity.
So gravity and inertia are two different ways of looking at the same thing. Anything falling into a black hole will get stretched so that a unit of length increases but time then will also go slower ! It takes an infinite amount of time to pass through the event horizon.
I prefer to use rotational dynamics to derive tides on earth because they better explain the origin of the opposite tide and give quantitative answers – see my calculations here
lsvalgaard says: “The closer the Earth would be to the Sun, the faster it would go….”
That answers my last question…
(In Lief’s universe the slowest rockets reach the highest orbits!)
lsvalgaard says:
February 15, 2014 at 12:26 pm
Those are the formulas for fluid bodies. And, even though the Roche limit is relatively insensitive there, the shape the fluid assumes is quite sensitive. So, you’re no longer dealing with a spherical body. But, my equations for a spherical body are still correct. And, there is a significant effect.
Look higher at the rigid body calculation. You will see the factor of 2 change to the factor of 3 in the formula as I explained above.
It has an effect, just as I outlined. You are wrong.
Leif,
I’m pretty sure Clive Best (February 15, 2014 at 10:43 am) has it correct for tides on Earth. Yes, tidal forces on objects in free fall is exactly as Willis describes, but I think that explanation is not a very good one for Earth’s ocean tides. Please see Clive’s web page (http://clivebest.com/blog/?p=5572) for his complete derivation. The magnitude of the ocean tides on Earth is too large to be accounted for by Willis’s classic free-falling-object explanation. Clive describes his background as follows:
“I have a Bsc in Physics and a PhD in High Energy Physics and have worked as a research fellow at CERN for 3 years, Rutherford Lab for 2 years and the JET Nuclear Fusion experiment for 5 years. Thereafter I worked at the Joint Research Centre in Italy until April 2008 being seconded to the African Union in Addis Adaba Nov 2007 until March 2008.”
He does know a bit of physics; I would not discount what he says without looking at his derivation, which looks correct to me.
Mike M says:
February 15, 2014 at 12:40 pm
lsvalgaard says: “The closer the Earth would be to the Sun, the faster it would go….”
That answers my last question…
(In Lief’s universe the slowest rockets reach the highest orbits!)
Here you can learn about the orbital speeds of the planets and see that the closer they are to sun the faster they go: http://www.sjsu.edu/faculty/watkins/orbital.htm
Bart says:
February 15, 2014 at 12:45 pm
Look higher at the rigid body calculation. You will see the factor of 2 change to the factor of 3 in the formula as I explained above.
The factor increases because of the assumed rotation of the body [if you rotate the body fast enough it will break up just because of rotation], not because of orbital centripetal acceleration.
again: the orbital speed has no bearing on the tidal effects. From your link:
“As the orbit has been assumed circular, the total gravitational force and orbital centrifugal force acting on the main body cancel. That leaves two forces: the tidal force and the rotational centrifugal force.”
Steve Fitzpatrick says:
February 15, 2014 at 12:48 pm
Please see Clive’s web page (http://clivebest.com/blog/?p=5572) for his complete derivation.
If you go there, you will see that the orbital centripetal force omega actually falls out of the equation and it is never used for anything.
The magnitude of the ocean tides on Earth is too large to be accounted for by Willis’s classic free-falling-object explanation.
I don’t think so. As far as I know they are in the right ballpark.
Steve Fitzpatrick says:
February 15, 2014 at 12:48 pm
Please see Clive’s web page (http://clivebest.com/blog/?p=5572) for his complete derivation.
Tides are very important in astrophysics and is something we know a lot about. Here is my derivation of the tidal equation [the actual height of the tidal bulge], slide 21 of
http://www.leif.org/research/AGU%20Fall%202011%20SH34B-08.pdf
On slide 4 you can see the formula used to calculate the tidal effects of the planets on the Sun.
lsvalgaard says:
February 15, 2014 at 12:55 pm
“That leaves two forces: the tidal force and the rotational centrifugal force.”
And, the “rotational centrifugal force” to which they refer is embodied in the equation below which, as you see, depends on the orbit rate. Why? Because their body is tidally locked.
This treatment is, in fact, precisely equivalent to what I have written. It is just another way of writing the same thing for a specific scenario. You do not understand it, so you jump to conclusions. But, the bottom line is that the orbital rate does have an effect.
Really, Leif, this is elementary. You aren’t even close to being right here. Give it up.
lsvalgaard says:
February 15, 2014 at 1:07 pm
“On slide 4 you can see the formula used to calculate the tidal effects of the planets on the Sun.”
A very different situation than the one we are exploring. The effect of centripetal acceleration is, indeed, negligible here. Why? Because the Sun is massive, and the barycenter is close to the center of the Sun. The Sun does not orbit the planets, but the planets can very nearly be said to orbit the Sun.
Similarly, centripetal effects are very small on lunar tides – the Earth does not orbit the Moon. But, we are talking here of solar induced Earth tides.
Lief says
It drops out because inertial mass = gravitational mass. This mystery was eventually explained by Einstein and it was gravity that turned out to be in some sense the fictional force!
Centrifuges separate U256 from U238. Nobody told the machines that what they were doing was fictitious or impossible. The engineers observing them working from the lab – an inertial external frame – didn’t stand around scratching their heads wondering how the hell it all works !
Lief,
So do you disagree also with the Wikipedia description of lunar driven tides on Earth?
“The plane of the Moon’s orbit around Earth lies close to the plane of Earth’s orbit around the Sun (the ecliptic), rather than in the plane perpendicular to the axis of rotation of Earth (the equator) as is usually the case with planetary satellites. The mass of the Moon is sufficiently large, and it is sufficiently close, to raise tides in the matter of Earth. In particular, the water of the oceans bulges out towards the Moon. There is a roughly opposing bulge on the other side of Earth that is caused by the centrifugal force of Earth rotating about the Earth–Moon barycenter. The average tidal bulge is sychronized with the Moon’s orbit, and Earth rotates under this tidal bulge in just over a day. However, the rotation drags the position of the tidal bulge ahead of the position directly under the Moon. ”
Which leads to gradual (geologic periods) increase in the Moon’s distance from Earth and gradual slowing of Earth’s rotational rate. Like I said, Willis’s explanation is perfectly accurate for a free falling body, It just doesn’t seem to me a very useful description for the orbiting Earth-Moon (and Sun) system that generates Earth’s ocean tides.
clivebest says:
February 15, 2014 at 1:27 pm
I think you mean U235 from U238. (The only possibilities for natural Uranium are 234, 235, and 238).
Steve,
Yes indeed it should have been U235
Although God knows we could do with another energy source !
Oh dear !
http://www.leif.org/research/AGU%20Fall%202011%20SH34B-08.pdf
Triple Peak Periods of 9.91 yr [C], 10.78 yr, and 11.87 yr [J]
because in general we have:
cos α + cos β = 2 cos [(α + β)/2] cos [(α − β)/2]
So, the sum of two
cosines can be written
as the product of two
cosines [‘amplitude
modulation’].
====
Hopefully Willis will be along soon to explain how Leif is making a fool of himself , how dare he make up all this “bullshit” and he’d better damn well explain it, or else……
I used to firmly believe all that crap too until Willis put me straight. Good job he’s around.
stevefitzpatrick says:
February 15, 2014 at 1:27 pm
“There is a roughly opposing bulge on the other side of Earth that is caused by the centrifugal force of Earth rotating about the Earth–Moon barycenter.”
I disagree with that. The bulge would exist regardless of centrifugal “force”. Centrifugal force simply adds to the effect.
Gravity is stronger on the near side than it is at the center, so it draws material on that side toward the focus of the orbit. It is weaker on the far side than it is at the center, so the material on that side is drawn in the other direction.
Similarly, centrifugal “force” on the near side is weaker than it is at the center, so material on the near side is drawn away towards the focus of the orbit. Mutatis mutandis on the far side.
The Wikipedia description appeals to intuition, because we thing of gravity as pulling into the center, and centrifugal force as pulling away. But, that is erroneous, because all the pushing and pulling is with respect to the central of gravity of the orbiting object.
Leif,
I think a quick though experiment will settle it. Imagine for a moment not an orbiting Earth-Moon system, but Earth and Moon fixed relative to each other, but held apart at a fixed distance by a (very strong!) mass-less rod. What would happen to the ocean? It would bulge (become deeper) on the Moon side of the Earth, and at the same time become more shallow on the side opposite the Moon. Not two bulges, only one. It is the joint rotation about the Earth-Moon barycenter that generates the opposing bulge away from the Moon.
Bart says:
February 15, 2014 at 1:40 pm
Please consider my thought experiment described above. Centrifugal forces around the barycenter seem to me key to the actual tidal behavior of the Earth’s oceans.
.Mike M says: February 15, 2014 at 12:21 pm …. So if earth’s orbital velocity around the sun slows down it will not fall closer towards the sun and if it speeds up it won’t go further way from the sun? …
—————————
lsvalgaard says: …The closer the Earth would be to the Sun, the faster it would go …
—————————
You avoided answering the question.
My ORIGINAL question: If earth’s orbital velocity around the sun slows down it will:
A) Go closer to the Sun
B) Go further away from the Sun
Answer the question, A or B?
CliveB: Centrifuges separate U256 from U238. Nobody told the machines that what they were doing was fictitious or impossible.
If you climb in with the gas and start spinning you will need to invoke a _fictitious_ force to explain why you are being thrown against the wall of the centrifuge.
If you watch from the lab you will explain that the walls of vessel are providing the centripetal force needed to constrain the gases in a circular motion. Nothing fictitious needs to be explained to the machines or the lab techs.
stevefitzpatrick says:
February 15, 2014 at 1:41 pm
“What would happen to the ocean? It would bulge (become deeper) on the Moon side of the Earth, and at the same time become more shallow on the side opposite the Moon. Not two bulges, only one. “
That is an inappropriately constrained analogy. The the rod is canceling the attractive force on the Earth via compressive forces.
In the case of pure gravity, the Earth is being pulled at one level. The oceans on the near side are being pulled harder, and those on the far side are being pulled less.
The centrifugal “force” does not create the symmetry in the bulge, it only adds to it.
Bart says:
February 15, 2014 at 1:13 pm
And, the “rotational centrifugal force” to which they refer is embodied in the equation below which, as you see, depends on the orbit rate. Why? Because their body is tidally locked.
Fast rotation can also disrupt a body [nothing to do with tides]. One way of estimating the rotation period of a close-in body is to assume that it is tidally locked and then equal to the orbital period.
The combined effect of fast rotation and tidal forces makes the break up happen before it would without rotation. But the tides themselves have nothing to do with rotation or orbital motions. I have you a simple example of a non-rotating body falling straight into the Sun from infinity [no orbital ‘sideways’ movement. Calculate for us what the tidal height would be for that body and you will see where you go wrong [you get the same answer as the ‘standard’ tidal formula gives].
I know it is a difficult logical hurdle when you first approach these kinds of problems, but intuition largely fails in accelerated reference frames.
The Earth is, itself, being accelerated by gravity. Stress occurs not when objects are accelerated, but when they are differentially accelerated.
The amount by which materials on the near side are being accelerated faster than the solid Earth is the same as the amount by which objects on the far side are being accelerated slower. As a result, you get a symmetric bulge.
Steve Reddish says:
February 14, 2014 at 8:33 pm
1. Atmospheric contraction and expansion contribute to its tidal bulges, but not so for the oceans. Sea tides rise and fall solely due to the lateral flow of sea water.
===========
good point. water is largely incompressible. Thus its cannot expand or contract to create a tidal bulge. Thus, the water must flow in response to the tidal force.
This will affect the mixing rate. And due to the large thermal capacity of the oceans, even a small change in the mixing rate will have significant affects on climate.
So, if there is any long term cyclical behavior in the tides, and it is found to coincide with climate cycles, then tidal methods could provide a reliable mechanism to predict climate change.
Willis:
A very nice and clear explanation of the governing tidal force and how it is correctly derived. There are many poor examples out there which your example puts to shame.
Thank you.
I hope that you will agree with me though that this is just the tip of the iceberg.
How that force plays out on the real ocean surface and internally below that surface is where the complexity and interest really lies.
Bart,
“The the rod is canceling the attractive force on the Earth via compressive forces.”
Nonsense. The water on the surface of the Earth does not know anything about the existence of my imaginary rod. The water only reacts to net acceleration forces acting on it. What makes the second tidal bulge in an orbiting system is indeed centrifugal acceleration around the barycenter.
lsvalgaard says:
February 15, 2014 at 1:58 pm
Are you laboring under the presumption that I am claiming something along the lines of stevefitzpatrick, that the bulge is only symmetric due to the centripetal acceleration? If so, you can see that, that is incorrect from the recent posts.
Mike M says:
February 15, 2014 at 1:52 pm
“My ORIGINAL question: If earth’s orbital velocity around the sun slows down it will:
A) Go closer to the Sun
B) Go further away from the Sun
Answer the question, A or B?”
The answer you seek is in Google.
http://lmgtfy.com/?q=Speeding+up+and+slowing+down+in+orbit
https://howthingsfly.si.edu/media/speeding-and-slowing-down-orbit
“So, if there is any long term cyclical behavior in the tides, and it is found to coincide with climate cycles, then tidal methods could provide a reliable mechanism to predict climate change.”
what like lunar declination affecting Indian Ocean you mean?
http://climategrog.wordpress.com/?attachment_id=774
this comes from a movement of water in and out of tropical Indian.O.
http://climategrog.wordpress.com/?attachment_id=777
That implies non linear feedbacks in tropics compensate when warm water is moved in and out.
stevefitzpatrick says:
February 15, 2014 at 2:10 pm
“The water on the surface of the Earth does not know anything about the existence of my imaginary rod.”
Then, it is an alien entity which destroys the analogy. The water on the surface of the Earth clearly experiences the gravity field pulling on the Earth.
“The water only reacts to net acceleration forces acting on it.”
Acceleration relative to what? To the acceleration of the Earth. If your Earth is not accelerating, then your analogy is off the mark.
“What makes the second tidal bulge in an orbiting system is indeed centrifugal acceleration around the barycenter.”
Sorry, no.
RichardLH says: ,….
Reducing velocity AT A GIVEN ORBITAL RADIUS, (the whole basis of my contention) = less energy = go closer to the sun, (yeah, it will speed up tangentially because gravity is stronger but it’s overall orbital energy will be LOWER; it has to be.
RichardLH says: ,….
What do astronauts do to come back to earth? Speed up?
Bart says:
February 15, 2014 at 2:12 pm
Are you laboring under the presumption that I am claiming something along the lines of stevefitzpatrick,
I’m not sure what misconception you are laboring under, but to clarify things “consider a non-rotating body falling straight into the Sun from infinity [no orbital ‘sideways’ movement]. Calculate for us what the tidal height would be for that body according to what you are laboring under.
lsvalgaard says:
February 15, 2014 at 12:30 pm
“The closer the Earth would be to the Sun, the faster it would go, but the orbital speed has nothing to do with the tides.”
The closer the Moon to the Earth, the faster its orbit, and therefore the faster the change in its tides I am sure you would agree.
So nothing is a bit short of the true explanations. Sure the 24 hour – 0/1/2 tides rate does not change as that is Earth rotational but the rest does.
Bart,
OK you have convinced me; you will never understand this relatively simple problem. A deus.
Mike M says:
February 15, 2014 at 2:20 pm
“What do astronauts do to come back to earth? Speed up?”
Ar but now you ask a different question. How do I change my orbit so as to not stay in orbit but instead move into a elliptical path that crosses the Erath’s surface.
Mike M says:
February 15, 2014 at 2:19 pm
“Reducing velocity AT A GIVEN ORBITAL RADIUS, (the whole basis of my contention) = less energy = go closer to the sun, (yeah, it will speed up tangentially because gravity is stronger but it’s overall orbital energy will be LOWER; it has to be.”
Shall I just quote from the link I provided.
“Speeding up and slowing down in orbit works just opposite to what you might expect. The larger a spacecraft’s orbit, the slower the spacecraft travels. So if you wanted to pass a spacecraft just ahead of you, you would have to fire a thruster in a forward direction. This would decrease your orbital energy and drop you into a lower orbit, where you will travel faster! The “passing lane” in orbit is always lower.”
RichardLH says: February 15, 2014 at 2:26 pm “Ar but now you ask a different question. How do I change my orbit so as to not stay in orbit but instead move into a elliptical path that crosses the Erath’s surface.”
Nice dodge, I want come back DOWN! I fire RETRO rocket engines to SLOW my velocity and LOWER my orbit. Less energy = LOWER orbit. You want to deny that – go ahead.
Mike M says:
February 15, 2014 at 2:19 pm
Think of it like this. You have acquired some potential energy to get to a given orbit. If you fire a forward thruster you lose some of that energy. To stay in orbit you must therefore be closer to the surface. i.e. less potential energy from that previously given you by the rocket that got you there.
RichardLH says: February 15, 2014 at 2:29 pm
Shall I just quote from the link I provided.
“Speeding up and slowing down in orbit works just opposite to what you might expect. The larger a spacecraft’s orbit, the slower the spacecraft travels. So if you wanted to pass a spacecraft just ahead of you, you would have to fire a thruster in a forward direction. ”
—–
“In a FORWARD direction” = RETRO ROCKET = OPPOSITE the direction of travel = OPPOSITE direction of thrust that got you into orbit!
RichardLH says: …
So with all your links and education why can’t you just ANSWER the question?
“My ORIGINAL question: If earth’s orbital velocity around the sun slows down it will:
A) Go closer to the Sun
B) Go further away from the Sun
Hmmmm? A or B ?
Here is Feynman on the basic tidal force:
http://www.feynmanlectures.caltech.edu/I_07.html#Ch7-S4
There is of course no force on the mass at the planet centre:
http://www.feynmanlectures.caltech.edu/I_13.html#Ch13-S4
Mike M says:
February 15, 2014 at 2:40 pm
“My ORIGINAL question: If earth’s orbital velocity around the sun slows down it will:
A) Go closer to the Sun
B) Go further away from the Sun
Perhaps it will be clearer if you think about the Moon instead. The Moon is moving away from us to a larger orbit where it moves slower because it is gaining angular momentum [stealing it from the Earth’s rotation which is slowing down]. So if you slow down the Moon, the answer is A. But your question is ill-posed in the first place as you did specify what mechanism you had in mind.
Mike M says:
February 15, 2014 at 2:31 pm
“Nice dodge, I want come back DOWN! I fire RETRO rocket engines to SLOW my velocity and LOWER my orbit. Less energy = LOWER orbit. You want to deny that – go ahead.”
Indeed you do as I explained above. Less energy = LOWER orbit = higher speed. Strange isn’t it?
stevefitzpatrick says:
February 15, 2014 at 2:26 pm
“OK you have convinced me; you will never understand this relatively simple problem.”
It is too simple. Don’t you realize that? Do you really think I would not understand your very simple setup?
But, it bears no relationship to reality. This is a more subtle problem than you yet apprehend. A lot of newbies make the same mistake as you do here.
Mike M says:
February 15, 2014 at 1:52 pm
This is trickier to answer than you may think
Imagine that you could have a big rocket engine mounted in the sky with the exhaust upwards from the Earth. Imagine that you started this engine when the exhaust pointed in the orbital “forward” direction. You should then expect the Earth was slowing down, right?
Well, it will not slow down, it will fall closer too the Sun and the orbital speed will increase. So if you try to brake the orbital velocity of the Earth the speed will increase.
The only way to slow down the orbital velocity of the Earth is to push it forward. The Earth will then move further away from the Sun and the velocity will counter-intuitively slow down.
This is not only a theoretical possibility, it actually happens each time we send a rocket away from the Earth. If for instance a rocket is sent away with destination Mars, it will be sent in the orbital “forward” direction, and the recoil will then make the Earth fall a little bit closer to the Sun and the speed will increase a little bit
To sum up: Closer orbits means higher velocity, but we have to brake the orbital objects to speed them up.
/ Jan
So why is the orbital speed of Earth faster at perihelion? Or is that something different due to an elliptical orbit?
RichardLH says: Indeed you do as I explained above. Less energy = LOWER orbit = higher speed. Strange isn’t it?
It is NOT a higher speed AT the same orbital radius – that’s the WHOLE point!
Tom in Florida says:
February 15, 2014 at 2:57 pm
So why is the orbital speed of Earth faster at perihelion? Or is that something different due to an elliptical orbit?
Because the closer you are to the Sun, the faster you have to move [‘sideways’] to stay in orbit.
stevefitzpatrick says:
February 15, 2014 at 2:26 pm
“OK you have convinced me; you will never understand this relatively simple problem.”
Try these for an explanation which is very similar to Wills’s work.
http://co-ops.nos.noaa.gov/restles3.html
http://www.lhup.edu/~dsimanek/scenario/tides.htm
“It is important to note that the centrifugal force produced by the daily rotation of the earth on it axis must be completely disregarded in tidal theory. This element plays no part in the establishment of the differential tide-producing forces.”
The forces that arise from moving around the barycentre are tiny compared to those. In there as described above but swamped by all the rest.
Jan Kjetil Andersen says February 15, 2014 at 2:56 pm ” This is trickier to answer than you may think”
—
Mike M says:
February 15, 2014 at 1:52 pm
My ORIGINAL question: If earth’s orbital velocity around the sun slows down it will:
A) Go closer to the Sun
B) Go further away from the Sun
Answer the question, A or B?
—
Not ‘tricky’ at all …in the context of my explanation of a mass M on the equator going faster at midnight or slower at noon with respect to earth’s orbital velocity – the answer is A…. PERIOD.
The mass experiences more net force toward the sun at noon and less at midnight by virtue of the difference in its orbital velocity as imparted by the rotation of the earth. (The difference in gravity itself by difference of one earth’s diameter versus 93 million miles is miniscule as WIllis already calculated.)
Mike M says:
February 15, 2014 at 2:58 pm
“It is NOT a higher speed AT the same orbital radius – that’s the WHOLE point!”
But it is impossible to stay at the same radius with lower radial velocity. In this universe anyway.
As you move closer and closer to the Earth’s surface you will get faster and faster as you do. Like a skater bringing in their arms in a spin.
As the Moon gains energy from the Earth by the friction on the tides, it is moving further and further away as Lief says. More potential energy = less radial velocity = larger orbital distances.
Mike M says:
February 15, 2014 at 3:08 pm
“My ORIGINAL question: If earth’s orbital velocity around the sun slows down it will:
A) Go closer to the Sun
B) Go further away from the Sun
Answer the question, A or B?”
If it has a lower orbital radial velocity (and therefore higher potential energy to be stable) it will be B.
If it has a higher orbital radial velocity (and therefore lower potential energy to be stable) it will be A.
As noted in the link above, you fire a forward thruster to loose height but gain orbital speed and vice versa.
We can think of the of the Sun and earth or the earth and moon being stationary at small point in time would the earth not have a bulge nearest the moon and furthest from the moon at this small instant of time.I think it would.
I just dropped in to see what condition my condition was in.
I considered the gravitational force between two bodies and the centrifugal force of one rotating around another with a fluid surface of the smaller. This is where the discussion seemed to move to even though Willis’ original post was the attraction of a non orbiting body to another.
The previous discussion has me concerned that I may not know sh*t from apple butter. I will not cook breakfast at home tomorrow but will instead eat @ a fast food restaurant w/ no apple butter.
Therefore my condition is unknown by me at this moment in time.
LOL
————-
Sorry mods, I post this comment on another thread by accident. My condition seems to be deteriorating.
RichardLH says: As noted in the link above, you fire a forward thruster to loose height but gain orbital speed and vice versa.
No.. not INITIALLY! Initially your velocity HAS TO slow down because you are DEcelerating! Yes, it speeds back up as you get lower and gravity increases BUT per my tidal assertion, you DO NOT get lower – you are staying within an earth radius of earth’s orbit around the sun.
The question about what will happen if a satellite “slows down” or “fires retro-rockets” is ill-posed. There are two different interpretations with two very different answers. Let’s assume the orbit is circular of radius “r1” to start with.
1) If on-board rockets are fired backwards briefly, the rocket will slow at that point in the orbit. It will stop orbiting in the circular orbit and orbit in an elliptical orbit with a semimajor axis r2 < r1. The time it takes to orbit will become less. It will have less overall energy, less average gravitational potential energy, and more average kinetic energy.
2) If on-board rockets are fired forwards briefly, the rocket will speed at that point in the orbit. If on-board rockets are fired forwards AGAIN briefly when the satellite reaches apogee so that it takes on a new circular orbit with r2 > r1, then the new orbit will have more average gravitational potential energy, and less average kinetic energy. The average speed over the whole orbit will decrease. (Rather counter-intuitive that your can fire the rockets forward TWICE and still end up with less KE!)
Basically, you have to know if you are forcing the satellite back into a circular orbit or not.
Interesting bit of trivia — for circular orbits, the potential energy is always twice the magnitude and opposite in sign to the kinetic energy.
RichardLH says: But it is impossible to stay at the same radius with lower radial velocity. In this universe anyway.
No – not when you’re stuck to earth by 10 m/sec^2 gravity it isn’t impossible.
It is fun to try to wrap (or would it be warp) my mind around all these ideas.
But something keeps nagging me…
Why is the rope blue ?
Tim Folkerts says: February 15, 2014 at 3:35 pm
The question about what will happen if a satellite “slows down” or “fires retro-rockets” is ill-posed. There are two different interpretations with two very different answers. Let’s assume the orbit is circular of radius “r1″ to start with.
1) If on-board rockets are fired backwards briefly, the rocket will slow at that point in the orbit.
…………………
STOP! Right there! … that’s all I was ever talking about!
Mike M says:
February 15, 2014 at 3:38 pm
STOP! Right there! … that’s all I was ever talking about!
and what has that to do with the tides that are around all the time.
Mike M says:
February 15, 2014 at 3:32 pm
“No.. not INITIALLY! Initially your velocity HAS TO slow down because you are DEcelerating! Yes, it speeds back up as you get lower and gravity increases BUT per my tidal assertion, you DO NOT get lower – you are staying within an earth radius of earth’s orbit around the sun.”
You seem to have a very strange view of the universe. It takes a while to catch up with what you do.
Unfortunately in the real universe, if you fire the thruster for a millisecond or an hour. the rate of change will happen instantaneously and so will velocity/height/etc.
If you can’t manage going down. Think the other way instead. As your rocket engine – now pointing along the orbit – pushes you forwards, you will slow down in forward radial velocity as you rise in height. The energy has gone into potential energy for height above the surface and thus lost from radial forward velocity.
Below stable orbital radial velocity you will of course get faster as you rise to it. It is what happens from then we are talking about.
lsvalgaard says:
February 15, 2014 at 3:41 pm
“and what has that to do with the tides that are around all the time.”
Nothing. But people don’t get how to manoeuvre in space at all. Most of the games have it wrong as well.
RichardLH says: “…will happen instantaneously and so will velocity/height/etc.”
Nope. You fire the rocket, your velocity increases as the rocket fires and THEN you start going up. As you go up, OVER TIME, your velocity then decreases until your reach a higher orbit at a lower velocity than that at which you started. You do NOT “instantaneously” change orbit altitude!
Mike M says:
February 15, 2014 at 3:51 pm
“Nope. You fire the rocket, your velocity increases as the rocket fires and THEN you start going up. As you go up, OVER TIME, your velocity then decreases until your reach a higher orbit at a lower velocity than that at which you started. You do NOT “instantaneously” change orbit altitude!”
Fire it for a millisecond in an hour and you will still see a change in orbit. Or are all the guys who fly in orbit wrong as well?
Mr. Eschenbach–
” In prior centuries, these atmospheric tides were said to affect the weather, although in a cyclical rather than a secular manner.” I am confused (or, Kung-Fu-sed, as my son’s karate teacher likes to say): I have never used “secular” in such a context as you have here. What does it mean here? (If you respond to this, thank you.)
William Larson says:
February 15, 2014 at 3:56 pm
I have never used “secular” in such a context as you have here. What does it mean here?
From the prayers IN OMNIA SAECULA SAECULORUM meaning [roughly] ‘for ever and ever’, thus ‘long-term’
Mike M says:
February 15, 2014 at 3:36 pm
“No – not when you’re stuck to earth by 10 m/sec^2 gravity it isn’t impossible.”
But you’re not in free orbit at that point. If you were to try and stay in free orbit just above the surface (1cm) you will need to have an airless planet and a very flat planet to achieve it. The required orbital velocity is just too great.
u.k.(us) says:
February 15, 2014 at 3:37 pm
“It is fun to try to wrap (or would it be warp) my mind around all these ideas.
But something keeps nagging me…
Why is the rope blue ?”
Cheapest on offer at K-Mart?
Mike M says:February 15, 2014 at 3:38 pm
STOP! Right there! … that’s all I was ever talking about!
——————
lsvalgaard says: February 15, 2014 at 3:41 pm and what has that to do with the tides that are around all the time.
————–
So you forgot? I didn’t Let’s go over it shall we? – you never answered the question:
My question: If earth’s orbital velocity, (AT IT’S CURRENT ORBIT), around the sun slows down it will:
A) Go closer to the Sun
B) Go further away from the Sun
Answer the question, A or B?
Still waiting for an answer FROM YOU. (And when you can give a straight answer.. THEN we’ll move on to explaining more to you .)
Mike M says:
February 15, 2014 at 4:06 pm
(And when you can give a straight answer.. THEN we’ll move on to explaining more to you .)
That is very generous of you. But, as I said, your question is ill-posed and borders on nonsense, so you perhaps see my problem…
RichardLH says: …airless planet and a very flat …”
You’re missing the whole point. The orbit is earth around the sun, the thing stuck by earth’s gravity is NOT in orbit around earth, IT IS EARTH! Specifically a drop of water at the equator.
lsvalgaard says: “..perhaps see my problem…”
Yeas I do – you’re obstinate.
The answer is A and it happens to a mass M sitting on earth’s equator at noon – it’s going SLOWER than earth’s overall orbital velocity.
On the other side, at midnight, it is going FASTER than earth’s overall orbital velocity.
The slower particle gets dragged in more by the sun and the particle going faster is being flung away from the sun.
Now disprove it directly instead of trying to weasel around it. Did I state something that is not true?
Mike M says:
February 15, 2014 at 4:15 pm
Now disprove it directly instead of trying to weasel around it. Did I state something that is not true?
You have discovered the amazing fact that the Earth’s rotation [measured on a mass sitting firmly and fast on the equator] goes in the same direction as the orbital movement as midnight and in the opposite direction at noon. Fascinating! Now what has that to do with tides?
lsvalgaard says: Fascinating! Now what has that to do with tides?
What I already explained above but I guess you have a short attention span.
February 15, 2014 at 7:13 am: A quick look gave me a result for a “no moon” variation of “midnight fling” acceleration over average center V^2/R of 3%. For now I’d say it looks significant.
Earth’s average orbit velocity V1 as 29885 m/sec. Crust WRT center V2 as 463 m/sec. So combined velocity in orbit around the sun at midnight V1+V2=V3 as 30349 m/sec V3^2 / V1^2 = 1.03
February 15, 2014 at 7:51 amBoiling it down, I’ve produced a two bulge tide model with no moon at all. Earth to Sun acceleration due to gravity is .006 M/sec^2 Plus 3% at midnight, minus 3% at noon makes it a change plus or minus .0002 m/sec^2 against our earth gravity of 10M/sec^2
Certainly tiny WRT to earth’s gravity at sea level but how much does that contribute to the formation of two lobes?
I’m stating that the difference EXISTS. Are you stating that it does not exist? Are my numbers way off?
Mike M says:
February 15, 2014 at 4:09 pm
“You’re missing the whole point. The orbit is earth around the sun, the thing stuck by earth’s gravity is NOT in orbit around earth, IT IS EARTH! Specifically a drop of water at the equator.”
Then the majority of the forces operating (to the first quite a lot of decimal places) will be the frictional, compressive, etc. components from the bits on water on either side of it.
Then will come the various forces that come from the Earth’s rotation alone, centripetal, coriolis, etc.
Then will come the 3d Tidal vectors.
That should cover the top 10 decimal places or so.
Mike M says:
February 15, 2014 at 4:09 pm
Oops. Sorry – left out tidal currents etc.
Mike M says:
February 15, 2014 at 4:28 pm
I’m stating that the difference EXISTS. Are you stating that it does not exist? Are my numbers way off?
As Bart has said many times, I am a dummy, embarrassing myself constantly, so please explain to this dummy how your differences produce tides. And how you would explain tides if the Earth were not rotating. I guess you would say that on a non-rotating Earth there would no tides ‘flung’ around, but explain that in some more detail, please.
RichardLH says: February 15, 2014 at 4:29 pm “Then the majority of the forces operating (to the first quite a lot of decimal places) will be the frictional, compressive….”
If you say so… I’m only pointing out the change in net acceleration force that goes up and down twice a day at the equator without any moon at all and simply because of earths’ rotation slowing/speeding earth’s crust slower/faster than earth’s solar orbital velocity.
lsvalgaard to his credit compartmentalized it best – you will weigh .002 less at midnight and noon than you will at 6am or 6pm. (Females using spring loaded bathroom scales take note.)
I would think seismographs register this effect but it isn’t noticed because it’s a much longer period than an earthquake and the amount of change is so small it’s probably ignored.
Mike M says:
February 15, 2014 at 4:51 pm
I’m only pointing out the change in net acceleration force that goes up and down twice a day at the equator without any moon at all and simply because of earths’ rotation slowing/speeding earth’s crust slower/faster than earth’s solar orbital velocity.
So you are claiming that if the Earth were not rotation there would be no tidal effects…
Good news for the proverbial astronaut falling into a black hole: just be sure that you don’t rotate and you’ll not be shredded by tidal forces…
Mike M says:
February 15, 2014 at 4:51 pm
“I would think seismographs register this effect but it isn’t noticed because it’s a much longer period than an earthquake and the amount of change is so small it’s probably ignored.”
I think you will find that the Earth Tide, the bulge in the rock itself from the Moon and Sun is an order to two higher but….
http://en.wikipedia.org/wiki/Earth_tide
Mike M says:
February 15, 2014 at 4:51 pm
you will weigh .002 less at midnight and noon than you will at 6am or 6pm.
Here is get-rich scheme using your insight: buy gold at noon, e.g. 100 kg, file off 0.2 kg [=6 oz @ US$ 1300/oz = $7600], then sell the gold at 6 pm as it at that time will weigh 100 kg and recover what you paid for the 100 kg at noon, pocketing $7600/day. In a year that is almost $3 million [tax free].
lsvalgaard says: “So you are claiming …”
I did NOT discount or preclude other factors! Stop putting words into other people’s mouths!
lsvalgaard says: Here is get-rich scheme
Ummm, only an idiot would use anything but a MASS BALANCE scale for stuff like gold – works on the moon.
Wow. Leif never stops amazing me with his infinite patience here. I’d be into the whiskey by now.
Mike M says:
February 15, 2014 at 5:05 pm
I did NOT discount or preclude other factors! Stop putting words into other people’s mouths!
So, answer the question: if the Earth did not rotate would there be tidal effects? If so, how large would they be compared to the ones caused by rotation? Huge or tiny? Or don’t you know?
Mike M says:
February 15, 2014 at 5:07 pm
Ummm, only an idiot would use anything but a MASS BALANCE scale for stuff like gold
And Mother Nature does not do that when it comes to create tides. How do you know?
RichardLH says: “I think you will find that the Earth Tide, the bulge in the rock itself …”
Oddly, that’s what I generally guessed at above. ( February 15, 2014 at 12:15 pm)
lsvalgaard says: February 15, 2014 at 5:14 pm “So, answer the question: if the Earth did not rotate would there be tidal effects? ”
From the moon, of course.
I think there is a gross misunderstanding of “free fall”. Willis is correct in his analogy and may even underestimate his own clarity.. the planet is actually “free falling” and is plunging toward the sun as described in his picture. There is also a sideways motion (orbital velocity) so we (earth) manage to keep missing the sun as we fall into it. Since the sideways motion is perpendicular it has no effect on tidal force so we can ignore it and are left with only the free fall condition. So the bodies M1, M2 and M3 are each different distances from the main attractor so each has a slightly decreasing pull. Lets call the forces magnitudes of 3,2, and 1 .All are positive pulls toward the sun ( or moon) in this frame of reference. The closest is hardest, the middle less and the extreme even less again. so you end up with tension in the theoretical string (local gravity replaces the string) and this results in a front-side and back-side bulge relative to the middle . Rather simply presented I think.
Good one Willis!
Trying to bring in orbital and rotational centripetal force is not required and has insignificant affects.
lsvalgaard says: “And Mother Nature does not do that when it comes to create tides. How do you know?”
Ho do I know what exactly? How to spot non-sequitur blather?
Mike M says:
February 15, 2014 at 5:25 pm
“Oddly, that’s what I generally guessed at above. ( February 15, 2014 at 12:15 pm)”
I Googled it with much less effort (to get the value – I already knew it existed). As I said., an order of magnitude or two greater than the discovery you are looking at.
RichardLH says: “I Googled it with much less effort ”
Keep up the good work!
Kirk c says: “Trying to bring in orbital and rotational centripetal force is not required and has insignificant affects.”
Willis’ is pointing out a gravitational differential producing a difference of ~1.1 MICRO Newtons, (.0000011 Newtons) between two 1KG masses.
I’m pointing to a .0002 m/sec^2 difference in acceleration from a rotational induced difference in sun’s gravitational field which, for a 1 KG mass, is .0002 Newtons. Insignificant?
Mike M says:
February 15, 2014 at 5:42 pm
“Keep up the good work!”
Just to point out that it existed and was significantly greater than you were looking for……
I can’t see why you didn’t try that route first anyway.
And looked at the internal tide which is much more significant than all the stuff going on at the surface anyway.
It is amusing to see bright people communicating with such difficulty.
RichardLH says: I can’t see why you didn’t try that route first anyway.
Well I guess that’s just a difference between us. I always try to come up with my own answer first and then look to the answers by others to see if/how my answer compares. Just looking up stuff doesn’t put my brain in gear.
Mike M says:
February 15, 2014 at 6:12 pm
“Well I guess that’s just a difference between us. I always try to come up with my own answer first and then look to the answers by others to see if/how my answer compares. Just looking up stuff doesn’t put my brain in gear.”
I just like to order the stuff I look at I quantitate order first. Tend not to get lost in the minutia then 🙂
RichardLH says:
February 15, 2014 at 3:04 pm
From your link:
“At about 54.7° from the Earth-moon line, the vector difference in the forces happens to be parallel to the surface of the Earth.” http://www.lhup.edu/~dsimanek/scenario/Field_tidal.jpg
That’s an interesting geometry, focused at sqrt of 3 Earth radius away from the center.
Mike M says:
February 15, 2014 at 5:55 pm
“Trying to bring in orbital and rotational centripetal force is not required and has insignificant affects.”
I’m pointing to a .0002 m/sec^2 difference in acceleration from a rotational induced difference in sun’s gravitational field which, for a 1 KG mass, is .0002 Newtons. Insignificant?
Ok. but rotational is not tidal. the rotational is uniform and causes an average equatorial bulge in 360 degrees 24/7. without moon or sun then, the net sea level rise is constant . I agree there is probably some small Coriolis effect set up as well… but this is not really the point of the thread. “Pondering tides” was the title.. not, “Would there be ocean currents on a rotating non-orbiting body”
cheers
Mike M says:
February 15, 2014 at 5:31 pm
From the moon, of course.
So if the Earth did not rotate there would be solar tides?
Ulric Lyons says:
February 15, 2014 at 6:18 pm
““At about 54.7° from the Earth-moon line, the vector difference in the forces happens to be parallel to the surface of the Earth.” http://www.lhup.edu/~dsimanek/scenario/Field_tidal.jpg
That’s an interesting geometry, focused at sqrt of 3 Earth radius away from the center.”
That’s actually from Wiki as the url notes (and yes it is deliberately exaggerated).
http://en.wikipedia.org/wiki/Tide
Mike M says:
February 15, 2014 at 5:31 pm
From the moon, of course.
So if the Earth did not rotate there would be no solar tides?
Ulric Lyons says:
February 15, 2014 at 6:18 pm
““At about 54.7° from the Earth-moon line, the vector difference in the forces happens to be parallel to the surface of the Earth.”
You weren’t suggesting the geometry is wrong are you? The arrows are too long but that is all.
RichardLH says:
February 15, 2014 at 6:39 pm
“You weren’t suggesting the geometry is wrong are you? The arrows are too long but that is all.”
I was remarking upon the described 54.7° angle rather than the diagrammatic representation of it.
It makes a sqrt 2, sqrt 3, sqrt 5 sided triangle.
Ulric Lyons says:
February 15, 2014 at 6:54 pm
correction 1, 2, sqrt 3.
Ulric Lyons says:
February 15, 2014 at 7:08 pm
Third time lucky lol, 1, sqrt 2, sqrt 3.
Mike M says:
February 15, 2014 at 5:55 pm
I’m pointing to a .0002 m/sec^2 difference in acceleration from a rotational induced difference in sun’s gravitational field which, for a 1 KG mass, is .0002 Newtons. Insignificant?
Irrelevant as there is not tidal effect stemming from that as the rotation does not make any difference to the Sun’s gravitational field.
Thought I’d jump in here in case there’s any confusion about Mike M.
Not me.
Gene Selkov says:
February 15, 2014 at 3:55 am
Say what? You post up a cross-section of the moon that looks like it’s drawn by a sixth-grade schoolkid, with no provenance and no supporting data …
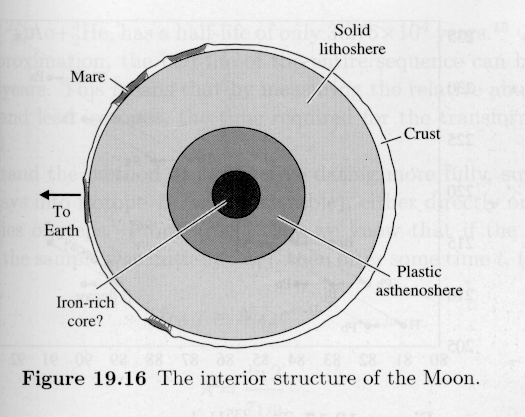
… and you claim that “falsifies” the Roche Limit and tidal elongation, both of which have been understood for centuries? Roche calculated the Roche limit in 1848. Do you think think that your pathetic citation”falsifies” it?
In addition, I find no evidence that either Metis or Pan are orbiting inside the Roche limit, see Wiki, which lists both Metis and Pan as orbiting outside the Roche limit. It also notes that Pan may be close to breaking up …
Absolutely not. However, I made up and used the example shown in Figure 1, because it is very useful for understanding the tidal forces. Plus I had great fun doing the drawings.
.
You are 100% correct. I used to produce and sell tide tables for the Solomon Islands based on my harmonic curve-fitting to generate the tables. Solomons has bizarre tides—for part of the year they have two tides a day, and for part of the year they have one tide per day.
Actually, that’s exactly what it means. How else do you explain two tides a day year after year over most of the planet, when both the sun and the moon only “go round” once a day? There are two tides because the slowly-changing tidal bulges stand still with respect to the much, much faster revolution of the earth. As a result, each part of the ocean goes past one of the bulges every twelve hours.
Or you could look at it the other way around, from an earth-centered point of view. Over a 24-hour period, the sun-moon pair go around the earth once. This drags the two tidal bulges around the planet, with two high tides occurring almost everywhere as a result.
Best regards,
w.
NoAstronomer says:
February 15, 2014 at 8:19 am (Edit)
You are correct. I was speaking of the situation shown in Figs. 1&2, not about the real earth. For the real earth, the total tidal force is the vector sum of the sun force and the moon force. Almost all the time, these are not in line with each other, and the resultant force occurs between them.
w.
Jan Kjetil Andersen says:
February 15, 2014 at 8:37 am
Sorry for the confusion. I thought it would be clear that if I’m describing a planet which is free-falling into the sun, that I was not talking about the earth. I’ve changed the head post to make this clear.
Thanks, Jan,
w.
lsvalgaard says:
February 15, 2014 at 5:04 pm
I know a better one:
Why not buy gold in Mexico City where the gravity acceleration is 9.776 m/s*s and sell it in Anchorage where the gravity acceleration is 9.826 m/s*s.
The difference is 0.5% so you can pocket 0.5 kg each time, not a tiny 0.2 kg.
Alas, the trick will not work for any of us with balance scales, as I think is the preferred method in gold trading.
Perhaps we should concentrate on answering Mike’s concrete question rather than evading to something that some may perceive as quite arrogant.
/ Jan
Kevin Kilty says:
February 15, 2014 at 10:05 am
Thanks, Kevin. As you will note in Figure 1 and Figure 2, the tidal effects do not depend in any sense on centrifugal acceleration. There is no centrifugal acceleration in the Figures, the masses and the planet are falling straight into the sun … and yet we still have tidal forces.
So any explanation that depends on centrifugal acceleration is incorrect.
Finally, it is not true that within a heliocentric frame of reference somehow the forces change direction. The tidal force is the difference between the gravitational forces GF1 and GF2, or GF2 and GF3. These gravitational forces are vectors—they have a strength (magnitude) and they also have a direction (straight towards the sun).
As as result, when you subtract one gravitational force from the other to get the tidal force, the tidal force also has a direction—which is also straight towards the sun.
Now, you can change the frame of reference all that you want … but that doesn’t change the direction of the tidal force vector. It always points towards the sun, no matter what your frame of reference might be.
Regards,
w.
Kirk c says: February 15, 2014 at 6:34 pm “Ok. but rotational is not tidal. ….”
Nothing of what you wrote had anything to do with what I’m asserting. You simply don’t understand. For any given particle orbiting the sun at a given radius from the sun there is an orbital velocity V with an inertial reaction of V^2/R acceleration EXACTLY EQUALING the gravitational pull it experiences from the sun at that orbital radius R. If it suddenly “finds” itself going slower it will be pulled toward the sun. If faster it will move away from the sun.
Such is what a particle sitting on earth’s equator experiences every day. The speed, S, the particle is traveling WRT to earth’s center is simply earth’s equatorial radius times earth’s angular velocity. From ~6am it begins slowing down from V (its component of solar orbital speed, being perpendicular to it rotational velocity spinning around earth at that time of day ), until noon when it reaches the point of maximum decrease, V- S, from solar orbit velocity and then speeds up again until ~6pm when its solar orbital speed is again back to V. Then it continues, now speeding up to V+S at midnight, the amount S more than solar orbital speed V.
When it is going slower than V it is pulled toward the sun by the amount of sun’s gravity which is, at noon, greater than the particle’s now reduced solar orbital inertial reaction (V-S)^2/R . When it is going faster by S at midnight than V it is being flung away from the sun by the increase of solar orbital inertial imbalance (V+S)^2/R which is greater than sun’s gravity.
I calculated the maximum differences in acceleration (V+S)^2/R or (V-S)^2/R versus V^2/R (which are actually slightly different in magnitude but beyond 5 places), as being -.00018 meters/sec^2 offset countering earth’s gravity occurring twice per day, at noon and midnight – two bulges.
For simplification I ignored the difference of R for each by the amount of earth’s radius as well as the sun gravitational field variation that WiIlis addressed which is a much smaller effect.
Is there an seismic instrument, appropriately damped to ignore earthquakes etc. and look only at the difference in gravity occurring over hours? If so it ought to record this effect and see a maximum gravitation pull being reached at 6am and 6pm with a minimum reached at noon and midnight with a difference by about .0002 meters/sec^s.
Clive Best says:
February 15, 2014 at 10:43 am
Well, that force is less than the tidal force by sin(theta). However, you’re missing a term. The problem with your equation is that at the poles in Figure 2, the tidal force is zero. This is because the tidal force depends on the difference in distance to the sun from a given point on the planet, and the distance to the sun from center of the planet. And at the poles, that difference is zero, so the tidal force is zero.
So at the same time that the horizontal force is increasing (by sin(theta)), the tidal force is decreasing (by cos(theta)). As a result, the horizontal component of the tidal force is
2 G m R sin(theta) cos(theta) / r^3
This has a maximum at 45°N and 45°S, which is one reason why the tides are big in those latitudes. However, the maximum is only half of the tidal force [ sin(45) * cos(45) = 0.5 ].
All the best.
w.
Willis,
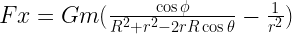


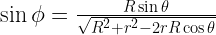
Yes you’re right
The correct equation is more complicated. Taking x as the direction from the centre of the earth to the moon and taking y the vertical axis then the net tidal force has 2 components.
where
and
The tractional force acting along the surface and therefore unaffected by the earth’s gravity is
Fy cos(theta) + Fx sin(theta) . The tractional force is zero at the central bulge and equal and opposite from either side.
Expat says:
February 15, 2014 at 11:28 am
Sorry, Expat, but that’s simply not true. As Figure 2 shows, you get two bulges with no centripetal force at all.
w.
Steve Fitzpatrick says:
February 15, 2014 at 12:48 pm
Steve, neither Leif or I are talking about actual tides on earth. We’re talking about how the tidal forces work on a planet. So whether Clive has it correct or not for the earth is material for a discussion of the actual Earthly tides … it means nothing to this discussion.
Willis Eschenbach says:
February 15, 2014 at 11:30 pm
“This is because the tidal force depends on the difference in distance to the sun from a given point on the planet, and the distance to the sun from center of the planet. And at the poles, that difference is zero, so the tidal force is zero.”
That is valid only 2 days a year for the sun due to earth tilt. All other days of the year is the “Sun tidal zero poles” not at earth geographics poles. Moon inclination will also have large impact on where on earth the “moon tidal force zero poles” are located. And also where on earth the maximum horisontal tide forcing are located. The horisontal forcing that actually move air and water according to Laplace.
That latitude change between 45°N and 45°S +/- 28.36°
In a cyclic way. 18.6 years the most obvious.
Some of the motivation for this article seems to be to dismiss my comment of a couple of days ago: “The tide raising force acts in both directions (bulge on each side in the simplistic model)”
The context of that remark was to explain why Willis’ plot of variation in the magnitude of the tidal force was not correct. He was subtracting the lunar and solar forces at full moon.
His headline graph in that article only peaks once per year , while the tides peak twice per year.
http://wattsupwiththat.com/2014/02/09/time-and-the-tides-wait-for-godot/#comment-1569175
I pointed out the mistakes and provided a modification for his R-code to give the correct addition of forces and a graph that produces the twice per year variations.
So does Willis correct his code and update the graph?
No, he writes another article to insist that he’s right, ridicules my comment and calls me a fool.
The fact that his tidal forces only peak once a year should be a clue to him, but I’m sure there’s a good reason to ignore that too.
As I said above, “You cannot stretch a body with one force” You can accelerate a body with one force. You need to separate the two effects.
http://wattsupwiththat.com/2014/02/14/canute-ponders-the-tides/#comment-1568736
You cannot stretch a body with one force.
In the case above (GF3+GF1)/2 = GF2 will accelerate each of the three tethered weights at the common rate towards the sun.
Two opposing forces (GF3-GF1)/2 will act at each end mass acting to stretch the tethers applying a tensional stress to the ensemble.
The lay reader may wish to decide whether to be guided by Willis or Feynman on this question.
http://www.feynmanlectures.caltech.edu/I_07.html#Ch7-S4
“The result of this imbalance is that the water rises up, away from the center of the earth. On the near side, the attraction from the moon is stronger, and the imbalance is in the opposite direction in space, but again away from the center of the earth. The net result is that we get two tidal bulges.”
Both sides in this argument are correct. You don’t need to use the centrifugal force to derive the formula for tides. This is because there is a perfect balance between the centrifugal force and the gravitational force at the center of the earth when in orbit around the earth-moon barycenter. This balance also determines the strength of tides on earth. When in doubt see what Feynman says.
So a body in free fall into the sun experiences ever increasing tidal forces until it is torn apart. A body in orbit however experiences regular varying tidal forces depending on the eccentricity of the orbit.
So on a purely logical basis Willis is correct. But in order to calculate the variations of tides on earth you need to include orbital dynamics because they change the earth-moon distance.
The formula: “Tidal Force = 2 * G * sunmass * r / D^3” is wrong. This is the formula for the “Tidal acceleration”. To make it a tidal force, you need to have another mass. The usual way it’s written is with m for the little mass (you used 1kg masses before) and M for the big mass (the sun):
Tidal Force = 2G m M r/D^3
The sentence “It’s not because the tidal force acts in different directions, because tidal force is always directed towards the sun.” is incorrect. On the side nearest the sun, the tidal force is directed towards the sun and moves the water towards the sun. On the side away from the sun, the tidal force is directed away from the sun and moves the water away from the sun. It should be clear that these are opposite directions. On the other hand, it is true that the “gravitational force” is always directed towards the sun. Maybe that was the source of some confusion. “Tidal forces” are defined with respect to the center of mass of the body (earth in this case), not the gravitating object.
On “Eventually, at a distance called the “Roche limit”, the tidal forces can reach such strength that they rip the planet into pieces …” it might be useful to note that the Roche limit is achieved when the tidal forces exceed the gravitational force of the planet. This makes it clear that “tidal forces” have to act oppositely on opposite sides of the planet — as does the planet’s gravitational force. In fact, I got the impression that someone reading the article might conclude that tidal forces should cause people on the sunny side of the planet to fall off of the planet. The reason this doesn’t happen is that the tidal force is smaller than the planet’s gravitational force.
By the way, I teach this subject.
there is a correct explanation of tides, written by some scientists involved in that kind of thing, here:
National Oceanic and Atmospheric Administration
http://tidesandcurrents.noaa.gov/restles1.html
Carl Brannen says:
February 16, 2014 at 2:10 am
Carl, I calculated (as is common) the force on a 1 kg mass. So I could have written
Tidal Force = 2 G 1 M r/D^3
You happy now? It doesn’t make any difference to me.
That sounds good, Carl … but I’ve given the mathematical derivation above. Now if you have a mathematical derivation that yields a force that points away from the sun, then please, break it out.
Well … no. For example, the Roche limit is different for liquid and solid planets … how could that be if the only relevant limit is the gravitational force holding the planet together?
In fact, as a moment’s reflection will confirm, the tensile strength of the planet is also part of the calculations of where a planet will break up …
Since the claim about the Roche limit is wrong (e.g. a planet which is a giant diamond would have a different Roche limit than a liquid planet), no, it doesn’t “make it clear”.
Gosh … does that prove that you must be right? Now I’m really impressed.
In any case, I await your mathematical derivation of the force that pushes the water away from the sun, or as you put it:
That’s big news, Carl, that there exists a repulsive gravitational force, that instead of attracting the water towards the sun, actually moves the water away from the sun … that’s a neat trick. Break out the math, so we can see how that works. You teach this the subject, surely you can bring forth the math that substantiates your claim of gravitic repulsion …
w.
Ulric Lyons says:
February 15, 2014 at 6:54 pm
“I was remarking upon the described 54.7° angle rather than the diagrammatic representation of it.
It makes a sqrt 2, sqrt 3, sqrt 5 sided triangle.”
I hadn’t noticed that. Thanks.
Asmilwho says:
February 16, 2014 at 2:17 am
“there is a correct explanation of tides, written by some scientists involved in that kind of thing, here:
National Oceanic and Atmospheric Administration
http://tidesandcurrents.noaa.gov/restles1.html”
I know, I provided it to Willis on his previous thread about Tides. I don’t think it got through then.
And all this
“We must concentrate on the Tide Raising Force”
In an abstract way it IS interesting. But in a minutia sort of way really. How the planet reacts to that tiny force and the massive outcomes that occur here on the surface and below the surface is the real source of interest.
http://i29.photobucket.com/albums/c274/richardlinsleyhood/TheInternalTideatHawaii_zps7c7d5dbf.png
http://i29.photobucket.com/albums/c274/richardlinsleyhood/M2Tides_zps758f7faa.png
http://i29.photobucket.com/albums/c274/richardlinsleyhood/K1Tides_zps453d8381.png
clivebest says:
February 16, 2014 at 12:57 am
“The tractional force acting along the surface and therefore unaffected by the earth’s gravity is
Fy cos(theta) + Fx sin(theta) . The tractional force is zero at the central bulge and equal and opposite from either side.”
I have tried to point this out to Willis already.
The important thing here is that this tractional force is not a delta on a larger force, Gravity. That is what the vertical component Willis is so keen on concentrating on is. A delta, a small difference. One capable of affecting the planet in a way that is difficult to miss but a delta none the less.
The tractional or tangential to the surface force is NOT a delta. There is nothing opposing it. If operates in its full magnitude which makes it much more interesting IMHO.
Coldlynx says:
February 16, 2014 at 12:48 am
“That is valid only 2 days a year for the sun due to earth tilt. All other days of the year is the “Sun tidal zero poles” not at earth geographics poles. Moon inclination will also have large impact on where on earth the “moon tidal force zero poles” are located. And also where on earth the maximum horisontal tide forcing are located. The horisontal forcing that actually move air and water according to Laplace.
That latitude change between 45°N and 45°S +/- 28.36°
In a cyclic way. 18.6 years the most obvious.”
Again, something that has been pointed out to Willis before on another thread, by me and Greg.
On each occasion he has seen the force pattern, drawn on a vertically oriented globe and looked at it as though that was the true picture.
What he has never done is drawn the North Pole to South Pole line through that globe and considered how that changes the picture.
http://upload.wikimedia.org/wikipedia/commons/d/d8/Field_tidal.png
http://upload.wikimedia.org/wikipedia/commons/6/61/AxialTiltObliquity.png
Willis Eschenbach says:
February 15, 2014 at 11:41 pm
Steve Fitzpatrick says:
February 15, 2014 at 12:48 pm
“Steve, neither Leif or I are talking about actual tides on earth. We’re talking about how the tidal forces work on a planet. So whether Clive has it correct or not for the earth is material for a discussion of the actual Earthly tides … it means nothing to this discussion.”
Concentrate on what I’m talking about – not on how this is all relevant to the planet. We are off in la la land.
Asmilwho says:
February 16, 2014 at 2:17 am
Thanks for that link, Asmilwho. There is a famous line, “Science is the belief in the ignorance of the experts”, which I’d say applies to that explanation. Their graphic is below:

For the point “B” that is on the opposite side of the tidal creating body (the moon in their example), they say:
I disagree with their explanation entirely, because it claims that the tidal bulges are caused by centrifugal force exceeding the gravitational force.
To the contrary, as I show in Figure 2 above, the bulges are the result of differential gravitational attraction which simply “stretches” the planet-ocean system into more of a cigar shape (ellipsoid). Note that the same thing happens to the solid planet. It too is stretched by the tidal force into more of a cigar shape.
And since the bulges appear in the non-rotating system in free-fall shown in Figure 2, that means that centrifugal force cannot be the explanation for the bulges … so your citation is wrong. The explanation of the tidal bulges on both sides of the Earth is not centrifugal force. It is differential gravitational force.
There is a correct explanation of tides in the head post. If you think not, please tell me exactly where you think I’m wrong.
w.
Willis Eschenbach says:
February 15, 2014 at 11:30 pm
“And at the poles, that difference is zero, so the tidal force is zero.”
If, and only if, the Earth’s rotational axis and orbit were not tilted to the line of both of the items in question, the Moon and the Sun.
If everything was vertical, then things would be trivially simple and not nearly as complicate as they really are.
I have given this to Willis before
“And this for explaining why it is not due to centrifugal forces :-)”
http://www.lhup.edu/~dsimanek/scenario/tides.htm
And this provided by Greg, on the other thread about tides, about how the heat (missing or otherwise) dances to a tidal pattern down deep in the oceans when no-one is looking 🙂
https://sites.google.com/site/climateadj/argo-animations”
EDIT – damn ” got in there by mistake.
And this provided by Greg, on the other thread about tides, about how the heat (missing or otherwise) dances to a tidal pattern down deep in the oceans when no-one is looking 🙂
https://sites.google.com/site/climateadj/argo-animations
Add to that the earth moon barycenter is only average 1707 km below earth surface. Compare with earth radius of 6,371 km.
Coldlynx says:
February 16, 2014 at 4:03 am
“Add to that the earth moon barycenter is only average 1707 km below earth surface. Compare with earth radius of 6,371 km.”
You do have to keep a sense of proportion here though when talking about the barycentre. Sure the whole thing does revolve around that point. But at a rate that is 28 times slower than it is running round the Earth central spin axis.
So the effect is spread out over that much faster rate and the higher rate centripetal force is correspondingly that much higher as well. 28 times as much in fact.
clivebest says:
February 16, 2014 at 12:57 am
“Yes you’re right
The correct equation is more complicated. Taking x as the direction from the centre of the earth to the moon and taking y the vertical axis then the net tidal force has 2 components.
Fx = Gm( \frac{ \cos \phi}{R^2 + r^2 – 2rR \cos \theta} – \frac{1}{r^2})
Fy = \frac{ -Gm \sin \phi}{R^2 + r^2 – 2rR \cos \theta}
where
\cos \phi = \frac{r-R \cos \theta}{\sqrt{R^2 + r^2 – 2rR \cos \theta}}
and
\sin \phi = \frac{R \sin \theta}{\sqrt{R^2 + r^2 – 2rR \cos \theta}}
The tractional force acting along the surface and therefore unaffected by the earth’s gravity is
Fy cos(theta) + Fx sin(theta) . The tractional force is zero at the central bulge and equal and opposite from either side.”
There are three components to the tidal vector space as oriented to the Earth’s surface at any single point on that surface.
There is x, a vertical up and down vector that varies from 1 day to 1 year depending on Latitude.
There is y, a North/South vector that varies likewise
and z, an East-West vector that also varies likewise.
Now that will turn into a 3 channel, 3 colour normalised Mollweide projection movie of how this all varies over the 4 * 18.6 year solar/lunar cycle.
Any one with movie making skills out there?
RichardLH says:
February 16, 2014 at 3:16 am
I fear I don’t understand what you mean by “a delta on a larger force”. Usually, a “delta” means a change in something, that is to say the value at time 2 minus the value at time 1. Obviously, you are using “delta” in some non-conventional way.
And once again, you haven’t quoted what you disagree with, which makes it hard.
It seems that what you are calling a “tractional force” is the horizontal component of the tidal force. It is not a separate force. A force can be divided into a vertical and a horizontal components, but this is a vectorial representation, not separate forces. The horizontal and vertical components of the tidal force are real, but they are not separate forces.
At any instant, at two locations on the earth (points A and B in the graphic above), the tidal force is pointed directly vertically. Everywhere else, the tidal force is pulling at some angle to the surface. Using vectors we can divide this angled tidal force into a vertical and a horizontal component.
Very near the spots A and B in the graphic above, the tidal force is almost directly vertical, and the horizontal forces are smallest. Now given that, you’d think that near the north and south poles (top and bottom of the earth in the above diagram), the horizontal component of the angled tidal forces would be the largest. And you’d be right.
The problem is that as you move towards the poles, the horizontal forces indeed are a larger and larger component of the tidal force … but at the same time the tidal forces themselves become smaller and smaller as you move towards the poles.
This means that the horizontal component of the tidal force is strongest at 45°N and S. At that point, the horizontal component of the tidal force is half the total tidal force.
Now, of course on the real planet it is more complex, because the earth’s axis is tilted, and because the moon wanders above and below the ecliptic, and in and out as well, plus there’s the sun as well …
But none of that changes the fundamental relationships.
w.
Willis Eschenbach says:
February 16, 2014 at 4:42 am
“RichardLH says:
February 16, 2014 at 3:16 am
The important thing here is that this tractional force is not a delta on a larger force, Gravity. That is what the vertical component Willis is so keen on concentrating on is. A delta, a small difference. One capable of affecting the planet in a way that is difficult to miss but a delta none the less.
The tractional or tangential to the surface force is NOT a delta. There is nothing opposing it. If operates in its full magnitude which makes it much more interesting IMHO.
I fear I don’t understand what you mean by “a delta on a larger force”. Usually, a “delta” means a change in something, that is to say the value at time 2 minus the value at time 1. Obviously, you are using “delta” in some non-conventional way.”
No in its normal usage. That is a small relative change in a larger force. Sort of like ‘Normals’ rather than ‘Absolutes’!
EDIT: Make that No in its normal usage. That is a small relative change in a larger force. Sort of like ‘Anomalies’ rather than ‘Absolutes’!
Willis Eschenbach says:
February 16, 2014 at 4:42 am
“It seems that what you are calling a “tractional force” is the horizontal component of the tidal force. It is not a separate force. A force can be divided into a vertical and a horizontal components, but this is a vectorial representation, not separate forces. The horizontal and vertical components of the tidal force are real, but they are not separate forces.”
I was re-using the terms used by others so as to not add further complications….but you’re getting there.
“At any instant, at two locations on the earth (points A and B in the graphic above), the tidal force is pointed directly vertically. Everywhere else, the tidal force is pulling at some angle to the surface. Using vectors we can divide this angled tidal force into a vertical and a horizontal component.”
As I have been trying to point out to you for the last week or so.
“Very near the spots A and B in the graphic above, the tidal force is almost directly vertical, and the horizontal forces are smallest. Now given that, you’d think that near the north and south poles (top and bottom of the earth in the above diagram), the horizontal component of the angled tidal forces would be the largest. And you’d be right.
The problem is that as you move towards the poles, the horizontal forces indeed are a larger and larger component of the tidal force … but at the same time the tidal forces themselves become smaller and smaller as you move towards the poles.”
But now we are not adding or subtracting a small delta from a larger constant force. We are balanced on the centre of a see-saw. The slightest change around the centre will have a large effect on the position of the plank.
That is why you need to consider the 45-60 degree band as relative to the two orbital planes and its changes.
The force is not opposed by any other force.
Willis Eschenbach says:
February 16, 2014 at 4:42 am
“Very near the spots A and B in the graphic above, the tidal force is almost directly vertical, and the horizontal forces are smallest. Now given that, you’d think that near the north and south poles (top and bottom of the earth in the above diagram),”
WRONG. This is only true if the North/South Earth axis line is at the same angle as the orbital planes. That is only true for 2 days a cycle, one each for the orbital planes on Sun and Moon. That damn Saros cycle again!
http://upload.wikimedia.org/wikipedia/commons/d/d8/Field_tidal.png
http://upload.wikimedia.org/wikipedia/commons/6/61/AxialTiltObliquity.png
Willis: See
http://www.nfo.edu/tilt.jpg
But you knew that right?
Willis:
Let me try to come up with a presentation that you can see what I mean.
Take some heavy planks (like your buckets)
Align them vertically on the Earth’s surface suspended/pivoted in a gimballed/bungee cord sense so that they float just above the surface.
Assume that the Earth, Sun and Moon are orbit/spin axis wise aligned to start with.
Now watch the planks as things rotate.
At the Equator they bounce up and down on a yearly, monthly and daily pattern.
At the Poles they wave left to right (say) and bounce up/down on a yearly and monthly pattern.
At 54.7° angle to the orbital plane they only wave left/right on a yearly, monthly and daily pattern, no vertical bounce at all.
Now make the orbital planes and the spin axis how they are in reality and…..
EDIT: Damn it.
At the Poles they bounce up/down on a yearly and monthly pattern.
Jan Kjetil Andersen says: February 15, 2014 at 11:04 pm ” Perhaps we should concentrate on answering Mike’s concrete question rather than evading to something that some may perceive as quite arrogant.”
Thank you!!
Guest Post by Willis Eschenbach
“Short Post. You can skip this if you understand the tidal force. ……”
==============
You made it sound as if it were going to be a simple discussion. There have probably been a lot of lurkers on this one.
Willis: See Fig903d and its accompanying text of how the Moon’s declination causes variation in your simple plots above.
From the NGA (so as you don’t think this is some random site I have plucked from Google)
msi.nga.mil/MSISiteContent/StaticFiles/NAV_PUBS/APN/Chapt-09.pdf
http://msi.nga.mil
“As the planet free-falls into the sun, the near side of the ocean is pulled the most. So it moves the most, pulling away from the planet.”
No, water will not move vertically. Only horisontally. The bulges are result of water flow by the horisontal tidal forcing. Mr. Laplace got that right already in the 18th century.
http://en.wikipedia.org/wiki/Theory_of_tides#Laplace.27s_tidal_equations
In fact is the near side the place where it moves the least.
Greg, of course, the missing unit mass factor. Thanks for the reply, should have caught that myself.
clivebest says:
February 16, 2014 at 1:22 am
“You don’t need to use the centrifugal force to derive the formula for tides.”
As I have demonstrated in my previous comment, you do, and you don’t.
You do not need centrifugal “force” to get a symmetric bulge. The bulge occurs on both sides in equal measure because gravity is stronger on the near side than it is at the center, and it is weaker on the far side than it is at the center. Relative to the center, this produces stress inducing acceleration relative to the Earth center which is towards the gravitating body on the near side, and away from it on the far side.
You do need centrifugal “force” to get the precise formula, though the effect could be said generally to be second order. It is more important for solar induced tides on the Earth’s oceans than it is for lunar induced tides on the Earth’s oceans, or for other cases where the distance from the barycenter of the orbiting system, of the heavenly object experiencing tidal forces, is relatively small. The centrifugal “force” adds to the stresses which produce the tides because it is weaker on the near side than at the center, and it stronger on the far side than at the center. Because the centrifugal “force” is directed outward rather than inward, this has similar impact to the gravitational effect: stress inducing acceleration relative to the Earth center which is towards the gravitating body on the near side, and away from it on the far side.
Bart says:
February 16, 2014 at 9:26 am
“You don’t need to use the centrifugal force to derive the formula for tides.”
As I have demonstrated in my previous comment, you do, and you don’t.
No, Bart, the centrifugal force has nothing to do with it. You went very quiet when asked about calculating the tidal effect on a planet falling straight into the Sun [Willis’ example]. Try again.
Isvalgaard, you always appear to me more deliberative than you seem here. If one treats the rotating Earth-Moon system as an inertial frame, then the rotation of the frame does indeed have to do with the tides because of pseudoforces (centrifugal force) than appear on the left side of the equation of motion. You aren’t arguing with me on this point, but rather with Lagrange, Laplace, D’Lambert, and Geo. Darwin. Good luck with that.
Bart says:
February 16, 2014 at 9:26 am
For a full explanation of why centripetal is the wrong way to go see
http://www.lhup.edu/~dsimanek/scenario/tides.htm
“So what about those centrifugal forces so many books make such a fuss about? You’ll notice we never mentioned them in our simple explanation. Should we have?
Many misleading accounts of the tides result from a common confusion about centrifugal effects due to rotation. “
EDIT: Sorry should have been “why centripetal/centrifugal is the wrong way to go see”
RichardLH says:
February 16, 2014 at 5:23 am (Edit)
Richard, I have put several simplified situations up for discussion. As I have said over and over, these are NOT THE REAL EARTH. Please stop telling me ad nauseum that the real Earth is more complicated than the simplified systems under discussion in my post. I know that, Richard, truly I do. That’s why humans use simplified examples, to understand what’s going on in the simplified system BEFORE thinking about all the real-world complications.
Can we return to the subject under discussion, which are the horizontal and vertical components of the tidal forces? At the points nearest and furthest from the sun IN THE SIMPLIFIED FREAKIN’ SYSTEM SHOWN IN FIGURE 2, the horizontal component of the tidal force is approximately zero. In addition, this is where the tidal force is the strongest.
At the points nearest to the north and south poles IN THE SIMPLIFIED FREAKIN’ SYSTEM, the vertical component of the tidal force is approximately zero, what force exists is almost all horizontal. However, that’s also where the tidal forces are approximately zero.
Since the amount of the total tidal force is proportional to cos(latitude), and the horizontal component of that tidal force is proportional to sin(latitude), the horizontal tidal force is equal to the tidal force time sin(latitude) cos(latitude). This peaks at 45°N/S, at 0.5 times the tidal force. At both the equator and the poles IN THE SIMPLIFIED SYSTEM, the horizontal tidal force is zero.
w.
Interesting 2005 monograph on Tides and centrifugal force by the astronomer Paolo Sirtoli.
Analyzed from several different Reference Frames, all with the same result.
At many websites, but also in some textbooks, one finds plainly wrong explanations of the lunar and solar tides. In particular much confusion arises when authors try to explain the existence of the second tidal bulge, the one opposite to the Moon. Often they invoke the centrifugal force as an “explanation”. But centrifugal force is a fictitious force, and we can’t justify a real effect with a fictitious force, can we?
The necessary and sufficient reason for the tides is the fact that over the volume of the earth, the gravitational force (from Moon or Sun) has different size and direction over the earth’s volume as a result of the varying distance from the external body. This is the “differential” force, sometimes called the “tidal force” and is the gradient of the force due to the external body. The centrifugal force is required only when the gravitational problem is done in a rotating reference frame. Often it is incorrectly used, even when its use is appropriate to such a rotating frame. It is a quantity necessary for accounting purposes, without any real effect on tides.
We will demonstrate this by considering different reference frames, rotating and non-rotating. We will calculate the direction and the intensity of the total acceleration for just two trial points, the well known A and B in figure 2. They are, respectively, the sublunar point and the anti-lunar point. If the results are identical to the those emerging from the case in wich there is only the gravitational force, we may rule out the centrifugal force as necessary to explain tides.
Analysing the commonest incorrect explanation, we find that that confusion arises from the incorrect choice of the reference frame (RF). In physics, the first step to successfully deal with a problem, is the choice of the RF. If mistakes are made in this starting phase, one will surely arrive at plainly wrong results. In physics, as in many other systems, the “GIGO” rule applies: Garbage In, Garbage Out.
Another misleading thing is that to get the tidal field, we must subtract from the moon’s gravity a uniform force field. But we learned in college that when we deal with rotation, the fictitious forces are proportional to the distance from the rotation’s axis. So where does this uniform field arise? All this will be revealed in the examples which follow.
http://vialattea.net/maree/eng/index.htm
RichardLH says:
February 16, 2014 at 7:56 am
Richard, the point of my simple plots is to assist in understanding the basics of the system BEFORE we get to such complications as declination. Keep your mind fixed on Figure 2. I’m talking about the tidal forces on a non-rotating planet and ocean free-falling into the sun … patience, my friend. We may get to declination some day, but not today.
w.
yirgach says:
February 16, 2014 at 10:37 am
I can’t thank you enough for that, yirgach.
The link that you gave, to this discussion of the tides, is stupendous. It should be required reading for anyone interested in the subject. It examines the tides from a variety of frames of reference, complete with moving graphics, and it shows that all reference frames come to the same conclusion. For me the money quote was in the conclusion (emphasis mine):
Note that the fact that the earth is rotating on its own axis, or the fact that the Earth and Moon both rotate around their common center of mass, has absolutely nothing to do with tidal forces.
w.
PS—Curiously, while writing this it strikes me that one place where rotational forces would come into play is where a planet in free-fall into the sun is approaching the Roche limit. If it is spinning very fast, it will break apart sooner than a non-rotating planet … but other than that unusual situation, the rotation is immaterial to the tidal force.
Larry Niven wrote a short story based on this phenomena called “Neutron Star”. Of course, mentioning that in this context is something of a spoiler.
The tide opposite the Moon is from centripetal force as the Earth and moon revolve around their combined centre of mass.
Willis Eschenbach says:
February 16, 2014 at 11:22 am
The article essentially points out the fact that intuitive reasoning may be blindsided by reality.
You have to know enough to ask the right questions.
Thank you for providing that knowledge.
Servius (@Servius) says:
February 16, 2014 at 11:28 am
I would also recommend “Dragon’s Egg” by Robert L. Forward for a hard science look at life on a neutron star.
https://en.wikipedia.org/wiki/Dragon%27s_Egg
Willis Eschenbach says:
February 16, 2014 at 10:33 am
“Richard, I have put several simplified situations up for discussion. As I have said over and over, these are NOT THE REAL EARTH. ”
Fine. Except that you (and others) then try to draw direct conclusions from them. I am just trying to point out that you can draw no conclusions from them at all.
They are useful only to the point where they explain to others what they do may not properly understand.
Can you try and keep it to just that then and not reach further? Perhaps put a proviso up that this is NOT relevant directly to the Earth? An abstract talking point.
And not try in head posts to dismiss how others see that the complications are what make this relevant and interesting?
lsvalgaard says:
February 16, 2014 at 9:33 am
“No, Bart, the centrifugal force has nothing to do with it. You went very quiet when asked about calculating the tidal effect on a planet falling straight into the Sun [Willis’ example].”
No, Leif. You are trivially wrong. The equations are right up in my post above. The factor I get is shown in the Wiki page on the Roche limit.
I didn’t answer because it is already answered. The tidal effect for falling straight in is missing the additional component due to centripetal acceleration, so its a factor of 2 instead of 3.
Stop being stupid. Read the equations I provided. They are correct.
RichardLH says:
February 16, 2014 at 9:58 am
No, you are arguing against stevefitzpatrick’s position as detailed in his previous posts, and with which I specifically disagreed over a number of posts in reply. I think this is Leif’s misconception as well, and he refuses to read my previous post to see my position, and just assumes he knows my argument.
I do not know how many times I can say this with nobody paying any attention, but let me state quite clearly for the umpteenth time: THE CENTRIPETAL ACCELERATION IS NOT RESPONSIBLE FOR THE SYMMETRY OF THE TIDAL BULGE. IT WOULD BE SYMMETRIC REGARDLESS. THE CENTRIPETAL ACCELERATION MERELY ADDS TO THE BULGE.
This is very annoying. Read my explanation of what is happening before assuming you know it.
Willis Eschenbach says:
February 16, 2014 at 2:30 am
“That’s big news, Carl, that there exists a repulsive gravitational force, that instead of attracting the water towards the sun, actually moves the water away from the sun…”
No, no, no, no, no. This is an ACCELERATED coordinate system. The center of the Earth is accelerating toward the Sun. The differential acceleration of the ocean on the far side away from the Sun is, indeed, away from the Sun.
If does not mean that the ocean on the far side is being pushed away from the Sun. It means it is being pulled toward the Sun LESS than the Earth is being pulled toward the Sun. The net effect is indistinguishable from an incremental repulsive gravitational force, or rather, a less attractive overall gravitational force.
Willis Eschenbach says:
February 16, 2014 at 10:33 am
As in
“The 54+ year cycle gets a lot of airtime, because people claim it is reflected in a sinusoidal approximately 54-year cycle in the for example the HadCRUT temperature records.”
where you most definitely tried to link on of your toy, abstract, (over?) simplified discussions to draw very definite conclusion that others were WRONG, WRONG, WRONG (and called me lots of names into the bargain).
I am quite prepared to forgive and forget but please don’t patronise me.
I have to leave, so I’m going to leave a final note. My equations are right. My interpretation of what is going on is right. If anyone thinks I am wrong, then they are either themselves wrong, or are addressing an argument I am not making. So, read what I have written before you imagine you think you know what I am claiming.
what make this relevant and interesting?
Bart says:
February 16, 2014 at 12:27 pm
“RichardLH says:
February 16, 2014 at 9:58 am
No, you are arguing against stevefitzpatrick’s position as detailed in his previous posts, and with which I specifically disagreed over a number of posts in reply. I think this is Leif’s misconception as well, and he refuses to read my previous post to see my position, and just assumes he knows my argument.
I do not know how many times I can say this with nobody paying any attention, but let me state quite clearly for the umpteenth time: THE CENTRIPETAL ACCELERATION IS NOT RESPONSIBLE FOR THE SYMMETRY OF THE TIDAL BULGE. IT WOULD BE SYMMETRIC REGARDLESS. THE CENTRIPETAL ACCELERATION MERELY ADDS TO THE BULGE.”
As I have never, ever claimed otherwise you’ve lost me.
I have provided countless links to other web sites that show precisely just that outcome. centripetal/centrifugal forces are almost totally irrelevant in tidal calculations.
Do you read anything I post or do you just assume I wrong regardless?
Willis,
“Since the amount of the total tidal force is proportional to cos(latitude), and the horizontal component of that tidal force is proportional to sin(latitude), the horizontal tidal force is equal to the tidal force time sin(latitude) cos(latitude). This peaks at 45°N/S, at 0.5 times the tidal force. At both the equator and the poles IN THE SIMPLIFIED SYSTEM, the horizontal tidal force is zero.”
Have read about seventeen pages thoroughly in my trusty astronomy book so I’m closer to trust my views on this topic. You seem to be limiting this entire discussion as if drawn on a 2d graph and when you say “… the tidal force time sin(latitude) cos(latitude)” I have to stop right there. Where is the longitude in that equation? Because your “SIMPLIFIED SYSTEM” is strictly 2d and not a water-only Earth? Seems kind of right but in 3d it seems to fail. At the equator 45° either side of the zenith point would not the tangential be also 0.5 that way? And at 45°N 45°E would it not be 0.25. That doesn’t seem correct at all.
I seem to get this… tangentially, as “the tidal force time √(sin²(long.azimuth°) + sin²(latitude))”, a circle on the Earth’s surface 45° any direction from the zenith point (just assume 0°N 0°E to use longitudes) and there would be 1.0 tangentially, at the zenith point zero and at 90° any direction from zenith point once again, zero.
If so I’m now following what you are saying. If not, what do you disagree with? Didn’t see anyone else addressing that.
RichardLH says:
February 16, 2014 at 12:32 pm
“As I have never, ever claimed otherwise you’ve lost me.”
I was stating my position, not imputing yours. We are in effing agreement on this. Why are you arguing?
“centripetal/centrifugal forces are almost totally irrelevant in tidal calculations.”
No, they are not. There are not the largest contributor, in fact are insignificant for any but solar induced tides on the Earth. And, they are NOT the cause of the symmetry in the bulge.
But they are not insignificant. Read what I have written. The centrifugal “force” is stronger on the far side than on the near side. This causes additional tidal deformation.
A lot of the misconceptions on this thread arise from people trying to apply Newton’s laws in an accelerated coordinate system. Newton’s laws hold only in an inertial coordinate system. In an accelerated coordinate system, you must take account of the acceleration with respect to inertial space.
The Earth is accelerating towards the Sun. So, to get the net specific force acting at the surface of the Earth, you must subtract out the Earth’s acceleration towards the Sun. As I showed how to do up above, where I showed that the true effect of the centripetal acceleration is to increase the specific force acting on the near and the far side by 50%. This is for solar induced tides only, as only there is the distance to the barycenter approximately equal to the distance to the Sun. The effect is much less for lunar induced tides.
Bart says:
February 16, 2014 at 12:27 pm
I didn’t answer because it is already answered. The tidal effect for falling straight in is missing the additional component due to centripetal acceleration, so its a factor of 2 instead of 3.
Stop being stupid. Read the equations I provided. They are correct.
The issue being of concern was that of falling straight in and centripetal acceleration for that is not a concern, so you can keep your snide comments up where they belong. The correct derivation for the general case is the one I presented in slide 21 of http://www.leif.org/research/AGU%20Fall%202011%20SH34B-08.pdf
lsvalgaard says:
February 16, 2014 at 1:01 pm
You are fixated on your interpretation of tides on the Sun. I do not have a problem with that interpretation. As I have stated time and time again, centripetal effects are minscule there, because the barycenter is quite close to the center of the Sun.
The place where centripetal effects are not insignificant is solar induced tides on the Earth. I keep explaining this, and it seems you simply disregard it, and continue on, as though I am claiming something I am not. If “stop being stupid” is snide, then let me clarify: stop telling me I am wrong about something I am not claiming.
Bart says:
February 16, 2014 at 12:39 pm
“I was stating my position, not imputing yours. We are in effing agreement on this. Why are you arguing?”
Because you then say
““centripetal/centrifugal forces are almost totally irrelevant in tidal calculations.”
No, they are not. There are not the largest contributor, in fact are insignificant for any but solar induced tides on the Earth. And, they are NOT the cause of the symmetry in the bulge.”
So my “totally irrelevant ” translates into “No, they are not. There[sic] are not the largest contributor”
Who is disagreeing with whom?
—-
From the link I provided
Tidal trivia.
•Amplitude of gravitational tides in deep mid-ocean: about 1 meter.
•Shoreline tides can be more than 10 times as large as in mid-ocean.
•Amplitude of tides in the Earth’s crust: about 20 cm.
•The gravitational force of sun on Earth is 178 times as large as the force of moon on Earth.
•Ratio of sun/moon tidal forces on Earth is 0.465.
•Tidal stretch of human body changes its height by fraction 10-16, an amount 1000 times smaller than the diameter of an atom. By comparison, the stress produced by the body’s own weight causes a fractional change in body height of 10-2. [Sawicki]
•Tidal friction causes Earth days to lengthen 1.6 milliseconds/century. [Sawicki]
•Angular velocity of Earth’s axial rotation: 7.29 x 10-5 rad/s.
•Angular velocity of moon’s revolution around Earth: 2.67 x 10-6 rad/s.
•Earth polar diameter: 12710 km.
•Earth equatorial diameter: 12756 km.
•Difference between these diameters: 46 km.
•Difference between these radii: 23 km, or 0.4 %.
•Thickness of atmosphere, about 100 km.
•Centripetal acceleration at Earth’s surface due to Earth’s axial rotation: 0.034 m/s2
•Size of centripetal acceleration at Earth’s surface due to Earth’s circular motion around the Earth-moon barycenter: 3.3 x 10-5 m/s2.
RichardLH says:
February 16, 2014 at 1:12 pm
“•Centripetal acceleration at Earth’s surface due to Earth’s axial rotation: 0.034 m/s2”
Not talking about axial rotation. I am talking about revolution about the Sun.
“•Size of centripetal acceleration at Earth’s surface due to Earth’s circular motion around the Earth-moon barycenter: 3.3 x 10-5 m/s2.”
Earth-Moon>/b> barycenter. To the degree that the Earth’s orbit about the Sun is a circle, the centrifugal “force” precisely cancels the gravitational force. That is why you experience free-fall in orbit – there are zero net forces. For solar induced tides, the sensitivity to position away from the center of gravity of the Earth from centrifugal “force” is 1/2 of the sensitivity from gravitational force (I showed this up above). That is why the centrifugal “force” adds 50% to the gravitational forces affecting the tidal bulge.
The sensitivity from centrifugal “force” for lunar induced Earthly tides is much smaller, because the barycenter is actually within the Earth itself, a small fraction of the distance to the Moon.
I believe that most of the debate in this thread is due to the confusion between reference frames. Let’s consider the simple case of three small asteroids falling directly towards the sun but separated along a radial distance, following Willis’ model. Assume that the asteroids are small enough so that we can ignore gravitational attraction between them. Our point of view is on an observational platform a fixed distance from the sun, held there by rockets let us say, and our weight represents the gravitational attraction of the sun. We see the three asteroids falling towards the sun and separating as they fall due to the gradient in the gravitational field. Each has a different acceleration at any point in time due to the different radial distance of each. There is no tidal force; there is just three objects falling. Now add a cable connecting the two outer asteroids to the centre one and maintaining a fixed distance between them. The cables will be under tension so as to counteract the gravitational gradient of the sun. So there are only two forces, the sun’s gravity and the tension in the cables. There is nothing that we can call a tidal force.
Now let’s consider a different frame of reference and place ourselves on the centre asteroid. Here we are in free fall towards the sun and are thus weightless and so assume that there is no gravitational force, but we must explain why the two outer asteroids are moving away from us in opposite directions (back to the no cable case). We must invent a fictitious force to explain this. One that draws objects away from us in the two opposite directions and which we call the tidal force. Put the cable back and this force is balanced by the tension in the cable. It is only in this frame that we can properly talk of tidal forces.
With the revolving and rotating earth the situation is more complicated and there are other fictitious forces (centrifugal, Coriolis, etc) which make the calculations more complicated depending on the frame that we choose to view things. This is shown in detail in the Sirtoli link as given by yirgach. We also have the Earth’s own gravitational field, the moon as well as the sun, and the tensile strength’s of land and sea.
So we either have a gradient in the gravitational field(s) or fictitious tidal forces, but not both. I like this comment of Sirtoli “Those forces are called fictitious because they have no physical reality, they emerge only in accelerating reference frames. The only forces worthy of being called “real” are the four fundamental forces: the gravitational, electrical, strong nuclear and weak nuclear. No physical effect can derive from a fictitious force: we can always choose a reference system in which this force will disappear.” I wouldn’t put it quite this starkly but I believe that it supports my position that the so called tidal force is fictitious.
The bottom line: I think that Willis is using the term tidal force somewhat incorrectly although his explanation of the tidal effect is correct.
Let me clarify my position one last time, before I must depart.
When I say that the tidal bulge is symmetric due to either gravity alone, or centripetal acceleration alone, or both together, I mean that it is two-sided – it bulges on the near side AND on the far side, and both contributions result in symmetric, two-sided bulges.
The centripetal acceleration is not necessary for the bulge to be two-sided. It only amplifies the two-sided bulge beyond what it would otherwise be. It amplifies the specific force differential on the near and far side by near 50% when the distance to the barycenter is close to the distance between the bodies.
As the relationship between that force differential and the size of the bulge is nonlinear, that 50% increase does not result in a 50% increase in maximum bulge. But, the effect is not insignificant.
Bart:
Angular velocity of Earth around the Sun in radians per second = 1.99 × 10^-7 rad/s
Angular velocity of Earth’s axial rotation in radians per second = 7.29 x 10^-5 rad/s
A couple of orders of magnitude difference as I suggested before
Therefore
Centripetal acceleration at Earth’s surface due to Earth’s axial rotation = 0.034 m/s2
Centripetal acceleration at Earth’s surface due to Earth’s orbit around the Sun ~ 0.034 * (1.99/7.29)^-2 m/s2
or did I get something wrong?
EDIT: Damn it – fingers again
~ 0.034 * (1.99/7.29) * 10^-2 m/s2
Mike M says:
February 16, 2014 at 6:00 am
Oh you’re welcome,
I think you asked a very clear and logical question and you deserve an answer to it.
However, as I see it, you are wrong because the rotational effect from the Earth is cancelled by other effects.
You look at the speed on the Earth’s surface and add that to the orbital velocity at midnight and subtract it at noon. Very logical and intuitive, but I think it is wrong, because if you choose to look at the orbital effect that way you also have to take into account the orbits effects on the centripetal acceleration on the Earth’s surface.
An object on the Earth’s surface will have smaller angular velocity at noon than at midnight. At noon the arc of the Earth’s surface is in the opposite direction as the orbital arc. The angular velocity from the orbit is therefore cancelling out some of the angular velocity from the Earth’s rotation. This causes a reduction in the centripetal acceleration from the Earth’s rotation at noon.
At midnight they are in the same direction and you have the opposite effect.
This effect cancels out the change in orbital velocity.
Concerning your discussion on varying gravitation during the day, I think you are partially right; the Earth’s gravity is not absolutely constant around the clock. It varies with the tides but the variation is minuscule.
/ Jan
lsvalgaard says:
February 15, 2014 at 9:12 am
According to your ‘theory’ a pendulum clock should vary its ticking rate during the day and it does not.
==============
Why is that? We know that pendulum clocks loose time if moved to a higher elevation. According to wikipedia 16 seconds/day at 4000 meters altitude.
It would seem from this result that a pendulum clock on the equator would locally tick slowest during a full eclipse of the sun. Thus the pendulum clock should gain or lose time, depending on the tidal forces from the sun and moon. Though the effect might be small.
Since gravity and acceleration are equivalent, the same argument can be applied to the rotation of the earth. Pendulum clocks should run slower at the equator than the poles, though this is complicated by the equatorial bulge of the earth.
This paper calculates that a pendulum clock varies about 8ms/day due to the tides.
http://leapsecond.com/hsn2006/pendulum-tides-ch1.pdf
http://leapsecond.com/hsn2006/pendulum-tides-ch2.pdf
And in this paper the previous author examines the Allan variance using data from Pierre Boucheron’s mid-1980’s timing experiment with a Shortt free pendulum clock.
“Conclusion
With the best of conditions the effect of tides on
pendulum clocks can be seen directly in rate or
progressive time error charts (e.g., Fedchenko gravim
eters via George Feinstein). We have also
seen the effect of tides through F
ourier spectral analysis (e.g., Philip Woodward). In this section
we explored how an Allan deviation plot can be
used to see the effect of tides on a precision
pendulum clock.”
http://en.wikipedia.org/wiki/Shortt-Synchronome_clock
Recent accuracy measurement
In 1984 Pierre Boucheron studied the accuracy of a Shortt clock preserved at the US Naval Observatory.[3][17] Using modern optical sensors which detected the precise time of passage of the pendulum without disturbing it, he compared its rate to an atomic clock for a month. He found that it was stable to 200 microseconds per day, equivalent to an error rate of one second in 12 years, far more accurate than the 1 second per year that was previously measured. His data revealed the clock was so sensitive it was detecting the slight changes in gravity due to tidal distortions in the solid Earth caused by the gravity of the Sun and Moon.[18]
Canute Ponders The Tides Posted on February 14, 2014 by Willis Eschenbach
Short Post. You can skip this if you understand the tidal force.
A better heading would be Canute ponders the tidal force as the tides as commonly understood on earth alone are infinitely complicated.
Sticking to your analogy of the 3 1 Kgm masses in free fall into the sun.
presumably all launched at the same time , at the same initial velocity
You are basically saying the difference in distance between them will increase over time as they get closer to the sun as the gravity differential is different proportional to the distance between them.
If this is the radius of the earth for a sol sized attractor and they are starting at the distance of the earth from the sun.
The speed of the fall would have to be equivalent to whatever speed is keeping the earth in orbit so it would be pretty fast.
I don’t know if there would be time for a tide differential to develop before the earth would crash into the sun.
So the tide differential shown at the time we are discussing would have to match some previous condition to get us to this point in time.
At which previous time the 3 balls would have to have been released at different speeds
A bit like the tortoise and the hare really, I need better maths with these infinite regress problems that I don’t have yet.
So, its not a short post, Its not simple.
Centrifugal, centripetal forces are irrelevant for this post only.
I now understand that when ball B gets to where ball A was, Ball A is slightly further apart from ball B by Richard’s delta amount due to the fact that it has had a slightly stronger G working on it over that distance and has therefore traveled further.
This is called a tidal force in this thread but would be basically the force of different strength gravity.
I f the gravity was the same for all 3 balls they would never move apart no matter how fast they all were accelerating.
I don’t understand how one can be falling but not moving [as in orbit] thus giving a tidal force.
It like saying yes the gravity difference is working but there is no gravity angech 117/2/2014.
It might need the explanation of centripetal forces which is a way of saying infinitely falling and accelerating but not moving in position.
angech says:
February 16, 2014 at 3:38 pm
I don’t know if there would be time for a tide differential to develop before the earth would crash into the sun.
=========
light takes 8 minutes to make the journey. free fall time from earth to sun is 65 days.
angech says:
February 16, 2014 at 3:38 pm
I don’t understand how one can be falling but not moving [as in orbit] thus giving a tidal force.
==========
the earth is moving while in orbit. in effect, the earth is always “falling” towards the sun, but at the same time moving sideways fast enough so that it never hits the sun.
for example, face an object and take 2.5 steps backwards. This is your starting position. Now, take 1 step towards the object, then two steps sideways. If you originally started 2.5 steps from the object, you will end up still 2.5 steps from the object. Turn slightly to face the object. Take 1 step towards the object and 2.5 steps sideways, you are still 2.5 steps from the object. Repeat over and over, you are in orbit.
Jan Kjetil Andersen says: February 16, 2014 at 2:13 pm “.. I think it is wrong, because if you choose to look at the orbital effect that way you also have to take into account the orbits effects on the centripetal acceleration on the Earth’s surface.”
A centripetal force is one which acts solely perpendicular to the direction of a particle’s velocity at any given instant. Such can be gravity OR something mechanically pushing on it, (such as a road surface pushing sideways on a tire making the car turn). So, I’m unclear exactly what you are describing with – “the orbits effects on the centripetal acceleration on the Earth’s surface”?
“The angular velocity from the orbit is therefore cancelling out some of the angular velocity from the Earth’s rotation.” Easily small enough to ignore for the purpose of illustration. (And I think it adds to it. If earth was like mercury it would complete one revolution per year. Now start rotating it to get one full day per year and you get 2 revolutions – not zero.)
“This effect cancels out the change in orbital velocity.” For all of earth it does but no, we’re talking about the affect it has on individual particles such as molecules of water that will experience a net accelerational difference oscillating throughout the day and therefore react to that change as opposed to if the earth rotated once per year so all the particles experience a balanced solar gravity = V^2/R at all times, (not accounting for Willis’ affect).
“Pendulum clocks should run slower at the equator than the poles, though this is complicated by the equatorial bulge of the earth.” That’s true but that’s a uniform centrifugal effect throughout the day and therefore, as a constant, makes no difference to the effect I’m addressing. Going slower at noon and faster at midnight WRT to solar orbital velocity, at the equator, will cause the pendulum to go slowest at noon and at midnight by a maximum amount on the equator also decreasing to zero at either pole for the same reason that your the centrifugal effect does, because: V= Ω*(Requator) * cos(latitude). Both effects rely on earth’s rotation but one has nothing to do with the other.
William Sears says: February 16, 2014 at 1:35 pm
“Here we are in free fall towards the sun and are thus weightless and so assume that there is no gravitational force, but we must explain why the two outer asteroids are moving away from us in opposite directions (back to the no cable case). We must invent a fictitious force to explain this.”
False. Acceleration due to gravity does not mysticaly ‘go away’ just because you are in free fall – it acts upon the object no matter which way it goes or (excepting relativistic velocities) how fast.
So there is no fictitious force per your example – all three are being accelerated by a REAL gravitation force that varys per asteroid by how close it is to the sun.
Mike M, you say that because you are still viewing the situation in the first reference frame of my example. You have to put yourself on the falling asteroid. Your objection can be used to dismiss any fictitious force by simply refusing to put yourself in the non-inertial frame.
William Sears says: February 16, 2014 at 5:37 pm “You have to put yourself on the falling asteroid. ”
Okay – I’m on your asteroid & the sun is accelerating at me. So what? The sun’s gravity is still acting upon my asteroid and it upon the sun. THAT doesn’t go away in ANY interial frame of reference.
Everything you wanted to know about tides, but were afraid to ask …
http://www.lhup.edu/~dsimanek/scenario/tides.htm
via The Chiefio ..
“Mike M says:
February 15, 2014 at 12:15 pm
Let’s not forget that earth’s crust is extremely thin WRT earth’s diameter and is going to flex to “bulging forces” mostly at the equator along with the ocean. Could that explain why ocean tide varies the least at the equator and greatest at the higher latitudes by virtue that those regions of crust are not being bulged as much making the determination of which way is “downhill” at various times of the day rather complex.. ??”
Given the 299 comments to this blog I am not going to try to find if anyone has actually replied to your post – I could not find a response over the next 50 or so. However, that the ocean tides vary lest (in very general terms) at the equator is not due to the earth’s crust also bulging. The tides are created by the sun and moon, and to a minimal extent by other planets. But the displacement on the earth’s surface is greatly affected by the shape of the oceans and seas, both shore lines, continental undersea extensions and the ocean bottoms. A very important point is the natural resonance of the oceans. This could be any reasonable period but logic suggests that periods close to the moon’s or sun’s maximum/minimum attraction periods will tend to result in greatest effects, as will periods a multiple or submultiple of those timings. Thus if the natural period of a body of water is 12 ( or 6) hours it will resonate with the sun and solar tides will be important. If the natural period is 12.5 or 6.25 hours moon tides will be important.
Then think of what happens when you are holding a bowl full of water. As you struggle to hold it up you move the bowl slightly, and the water slops about. At the resonant frequency of the bowl + water it will slop about a lot, at a frequency of your shaking substantially different the slopping may be minimal. But notice what happens in the middle of the bowl. Water moves from side to side but not up and down. At the edges water moves up and down but not from side to side. If your hands are at the sides, water vertical movement will also be greater close to your hands, and minimal well away from your hands. Sea and ocean basins act like this.
Tide ranges are high in places like the Bay of Fundy, the Thames, the Hoogly because they are at the edge of the seas/oceans, and because the shape of the land magnifies the vertical movement. At mid-Pacific islands tidal ranges are low – water tends to just move very slightly sideways rather than up and down. The Mediterranean has a very low tidal range as it is just not the right shape for resonance, and you have Italy, Sicily, Malta, and the Greek islands all acting to damp any horizontal water movement. Port Philip is an interesting case – a near landlocked body of water with a single narrow entrance. From half tide through to high tide and on to half tide outside the entrance, water pours in through The Rip, and the tide rises inside Port Philip, at Port Melbourne, Geelong, etc. For the other half of the tidal cycle outside, through low water, water pours out, and the tide inside Port Philip falls. So high water inside and outside are out of phase by six hours, roughly.
“Willis Eschenbach says:
February 15, 2014 at 11:30 pm
This has a maximum at 45°N and 45°S, which is one reason why the tides are big in those latitudes. However, the maximum is only half of the tidal force [ sin(45) * cos(45) = 0.5 ].”
OK so the tidal forces are zero at the poles. Unfortunately your equation also means the force is zero at the equator. Remember Sin(0) * cos (0) = 0.
Perhaps this needs to be modified or explained better?
Mike M, “so what?” isn’t much of an argument and therefore I don’t see how I can help you, but I will give it one more try. Remember that in any reference frame you can only use what you can measure locally and that you can not look outside in an attempt to circumvent this, no matter how tempting. What the sun appears to be doing is irrelevant. Block it with a dust cloud if it bothers you. You are weightless and there is no local experiment that you can do to detect the existence of a gravitational field. But the other two asteroids are accelerating away from you. Explain this without bringing in knowledge that you do not have in this reference frame. Forget about any curvature of space arguments as we are dealing with classical physics here.
Mike M says:
February 16, 2014 at 4:39 pm
Going slower at noon and faster at midnight WRT to solar orbital velocity
============
the orbital speed of the earth around the sun is simply a change of reference field. Since the centrifugal force is exactly opposite the centripetal force (gravitational attraction of the sun) you can get the correct answer using the centrifugal force in place of the gravitational force.
As a tidal comparison consider two soft rubber balls that are mounted through their centres to rigid posts close to each other. Opposite electric charges are deposited on them so that there is a strong electrostatic attraction. There is no charge on the posts and assume that the charge on the rubber balls is uniformly distributed and immobile. The shape of the rubber balls will be distorted due to this attraction and the fact that they are pinned through their centres. But the distortion will only be towards the other rubber ball, stretched out on the near side and compressed on the far side. A nonlinear field is not even necessary in this case. A similar effect is seen by pinning a plasticine ball to a wall and letting gravity do the stretching.
I think that this is the subconscious picture in most people’s minds in trying to understand the tides and why the stretching occurs in two directions. This may also lead to the perceived need to use a centrifugal force explanation. It also shows why the celestial object must be in free fall (eg orbit or the direct falling example used by Willis) to get the tidal stretch in two directions.
I’ve been grappling with this tide issue for two days now. I fully understand what Willis has shown in free falling bodies under gravitational forces. Then when I apply my new found knowledge to a physical application of some liquid covered planet in orbit around a much larger body (sun) I am having difficulty scrubbing centrifugal force from the mix in adding to an appreciable bulge to the far side of the planet (away from the sun).
It will soon click (I hope) but my brain is being quite stubborn on the issue at this point.
====
Truthseeker says:
February 16, 2014 at 5:55 pm
Thanks for the link. That and others have helped.
BTW, the earth and the moon do not rotate around each other, or around the barycentre. The earth and moon are a two planet system, not a planet and satellite system.
This may sound like heresy, but I believe if you check you will find that the moon’s orbit is always concave wrt the sun, just as is the earth’s. I call upon that great scientist, Isaac Asimov, for support (see: http://en.wikipedia.org/wiki/Double_planet )
“Tug-of-war definition
Isaac Asimov suggested a distinction between planet–moon and double-planet structures based in part on what he called a “tug-of-war” value, which does not consider their relative sizes.[4] This quantity is simply the relationships between the masses of the primary planet and the Sun combined with the squared distances between the smaller object and its planet and the Sun:
tug-of-war value = m1⁄m2 × (d1⁄d2 )2
where m1 is the mass of the larger body, m2 is the mass of the Sun, d1 is the distance between the smaller body and the Sun, and d2 is the distance between the smaller body and the larger body.[4] Note that the tug-of-war value does not rely on the mass of the satellite or smaller body.
This formula actually reflects the relation of the gravitational effects on the smaller body from the larger body and from the Sun. The tug-of-war figure for Saturn’s moon Titan is 380, which means that Saturn’s hold on Titan is 380 times as strong as the Sun’s hold on Titan. Titan’s tug-of-war value may be compared with that of Saturn’s moon Phoebe, which has a tug-of-war value of just 3.5. So Saturn’s hold on Phoebe is only 3.5 times as strong as the Sun’s hold on Phoebe.
Asimov calculated tug-of-war values for several satellites of the planets. He showed that even the largest gas giant, Jupiter, had only a slightly better hold than the Sun on its outer captured satellites, some with tug-of-war values not much higher than one. Yet in nearly every case the tug-of-war value was found to be greater than one, so in every case the Sun loses the tug-of-war with the planets. The one exception was Earth’s Moon, where the Sun wins the tug-of-war with a value of 0.46, which means that Earth’s hold on the Moon is less than half the Sun’s hold. Since the Sun’s gravitational effect on the Moon is more than twice that of Earth’s, Asimov reasoned that the Earth and Moon form a binary-planet structure. This was one of several arguments in Asimov’s writings for considering the Moon a planet rather than a satellite.[4]
We might look upon the Moon, then, as neither a true satellite of the Earth nor a captured one, but as a planet in its own right, moving about the Sun in careful step with the Earth. From within the Earth–Moon system, the simplest way of picturing the situation is to have the Moon revolve about the Earth; but if you were to draw a picture of the orbits of the Earth and Moon about the Sun exactly to scale, you would see that the Moon’s orbit is everywhere concave toward the Sun. It is always “falling toward” the Sun. All the other satellites, without exception, “fall away” from the Sun through part of their orbits, caught as they are by the superior pull of their primary planets – but not the Moon.[4][5][Footnote 1]”
— Isaac Asimov”
So bear that in mind when quibbling as to whether the earth is falling into the sun, or the moon is falling into the earth, and whether or not tides wait for no man.
if you would understand tides, realize that any reference to ‘Centrifugal force’ is wrong. Also any reference to ‘inertia’. See: http://www.lhup.edu/~dsimanek/scenario/tides.htm
The general view from Earth is here:
http://chiefio.wordpress.com/2014/02/16/tides-vectors-scalars-arctic-flushing-and-resonance/
But even then, reality is more complicated and “things change”…
Thanks for that link willis
This was also helpful
http://www.lhup.edu/~dsimanek/scenario/tides.htm
To add to my comment above (February 16, 2014 at 8:06 pm)
I am only concerned with the force(s) causing the far side bulge on a non axial rotating planet in orbit around another much larger body. The only centrifugal force (if any) I need to clarify in my mind would be that due to the orbit around the sun.
Maybe to put it another way. Why is there no centrifugal force involved with regards to a planet’s orbit around a much larger body (sun).
If I tied a brick to a rope and spun it around my head it would produce an outward force (centrifugal force) that would need to be countered acted by the rope. If we relate that concept of the orbiting brick and rope to a planet (brick) and gravitational attraction (rope) and call it a tidal force then would it be fair to say that the tidal force is the net result of gravitational attraction combined with the centrifugal force all wrapped into one package?
Bart says:
February 16, 2014 at 1:09 pm
The place where centripetal effects are not insignificant is solar induced tides on the Earth. I keep explaining this, and it seems you simply disregard it, and continue on, as though I am claiming something I am not. If “stop being stupid” is snide, then let me clarify: stop telling me I am wrong about something I am not claiming.
Prof. Dale E. Gary, NJIT, has a good simple explanation that you could learn from:
http://web.njit.edu/~gary/320/Lecture12.html
A full [but lengthy] treatment is here http://www.gps.caltech.edu/classes/ge167/file/agnew_treat_tide.pdf
Yet another [elementary] derivation is http://oceanworld.tamu.edu/resources/ocng_textbook/chapter17/chapter17_04.htm
and finally here is a good explanation dispelling the influence of centripetal forces: http://www.vialattea.net/maree/eng/index.htm
AlecM says:
February 16, 2014 at 11:33 am
No, it is not. Read the links, especially the one posted here, or you could just read their conclusion.
w.
RichardLH says:
February 16, 2014 at 12:17 pm
Perhaps your world works that way.
On my planet, people commonly study simplified models of complex situations, precisely to draw conclusions from them Happens all the time, I’m in mystery why you think we can’t learn valuable lessons from simple models.
w.
wayne says:
February 16, 2014 at 12:32 pm
Ok … since you haven’t disagreed with me in any points, I’ll join you, and I’ll stop there as well.
w.
Dudley Horscroft says:
February 16, 2014 at 8:13 pm
Thanks, Dudley. Your misunderstanding seems to be that the “this” in your quoted words of mine doesn’t refer to the tidal force. In the paragraph above the one you quoted, the “this” is specified as “the horizontal component of the tidal force”, not the tidal force itself.
And indeed, the horizontal component of the tidal force is zero at both the poles and the equator.
w.
Bart says:
February 16, 2014 at 12:31 pm
Got it … so, can we assume that your method is from the ultra-new field of investigation called “Science By Assertion”?
I remember that one from the playground, where when someone says “you’re wrong”, you say:
There have been a number of citations posted saying that centripetal force is immaterial to tides … not just one, but a bunch. So when you continue to repeatedly claim that centripetal force is a player in the tidal game, you’re obviously either:
1. Not reading the links provided, or
2. Not understanding the links provided, or
3. Just not paying attention.
In other words, although I hate to say it … you’re wrong.
Leif provided links that back up the claim that centripetal force isn’t a player. Mosher did the same. Others did the same.
Or you could just read, and re-read, and read again, the conclusion to one of those many links that I posted above, viz (emphasis mine):
See the part where he says that centripetal forces “do not produce any tidal deformation”? He backs that up with pages of analysis, diagrams, and equations.
You back your claims up by repeating you’re wrong, you’re wrong, you’re wrong …
I know which one I agree with … but then, I’ve done the math.
eyesonu says:
February 16, 2014 at 9:39 pm
Nope. Centrifugal (actually centripetal) force is entirely separate from the tides. See my previous comment.
w.
Willis Eschenbach says:
February 16, 2014 at 11:56 pm
“On my planet, people commonly study simplified models of complex situations, precisely to draw conclusions from them Happens all the time, I’m in mystery why you think we can’t learn valuable lessons from simple models.”
OK. Then at least do it correctly. So as to allow understanding instead of confusion. I obviously need to put my teaching hat on and explain how I think that this would best have been done so that there would have been a lot less squabbling all round.
Let us start from a very simple concept. A nearly featureless Globe, oriented vertically in the orbit, with a constant depth ocean, and a big ‘pin’ stuck down into the surface at 0 Lat, 0 Long.
Derive the gravitation forces that apply from the field diagram as below
http://upload.wikimedia.org/wikipedia/commons/d/d8/Field_tidal.png
Fig 1.
Let us then take some pictures of that from 3 directions starting from the longest possible intervals and working down towards human time frames.
The pictures are
1. looking down on the Earth from above at right angles to the orbit around the Sun,
2. looking along the orbit with the Poles North/South
3. looking out along the line drawn fro the Sun though the Earth.
This gives us x, y, z
Let us just deal with the Sun first, no Moon at all.
And we start taking pictures. At 4 year intervals to start with and at the Periapsis in the below.
http://en.wikipedia.org/wiki/File:Seasons1.svg
Fig 2.
Now we can see the ‘pin’ in the centre for 3, and pointing at the Sun for 2 and 1.
We can now deal with that oblate spheroid that the Earth’s rotation gives. We can also point out that most of the flattening is in the rock because the water skin is so thin. So all the centripetal forces, spin and orbit can be dealt with before we get into other stuff.
Now we speed up to once a year. And the first complication shows up. The ‘pin’ does not stay steady. It moves around those field diagrams in Fig 1.
So we draw out the first small cycle. One at 4 years. Then we move to 4 times a Year. Describe what happens there.
Now we have done the Solar components. Time to add in the Moon.
I am sure you can get the rest. Or do I need to do the full slide and description set?
Now is that a better way to do it or not? You tell me.
Oops sorry, Skipped the 4 times a year step to get all the Solar components. Must remember not to hurry. Overlook things if we do.
Willis:
That http://www.lhup.edu/~dsimanek/scenario/tides.htm link. I gave it too you on the previous thread about tides. I gave it to you on this thread about tides. Three other people have given it to on this thread alone as well,
Steve Mosher, E.M. Smith, Truthseeker.
Is it not about time you referenced it as well?
Giving as it does quite a reasonable explanation of how this all works and dispels a lot of misconceptions.
Mike M says: February 16, 2014 at 4:39 pm
Going slower at noon and faster at midnight WRT to solar orbital velocity
============
ferdberple says: February 16, 2014 at 7:15 pm the orbital speed of the earth around the sun is simply a change of reference field. Since the centrifugal force is exactly opposite the centripetal force (gravitational attraction of the sun) you can get the correct answer using the centrifugal force in place of the gravitational force.
==============
“the centrifugal force is exactly opposite the centripetal force” – I’m asserting that that is NOT true for the particle at noon and at midnight.
Forget earth’s rotation and all the canceling ‘on-earth’ forces for a moment and just assume there are three independent particles P1, P2 & P3 all present at earth’s orbital radius R from the sun. At “T ZERO”, P1’s velocity, V, exactly match’s earth’s tangential/orbital velocity so it’s V^2/R inertial reaction matches the centripetal force of sun’s gravity to make a perfect orbit.
Now consider P2 which going exactly in the same direction as P1 but it’s velocity is, instantaneously, (we are at T ZERO), slower than V by an amount S so, P2’s velocity is (V-S). For P2 the sun’s gravity is GREATER THAN the centripetal force needed to cause P2 to track the trajectory of earth’s orbit.
Left on it’s own, P2’s trajectory would decay from earth’s orbital trajectory toward the sun but we’re not going to allow it to do that… we’re going to add an outward acceleration, M, (away from the sun) to balance against sun’s gravity to make the centripetal force on P2 that required to keep P2 on earth’s orbital trajectory despite it’s slower speed. (Ask Buzz Aldrin what you do with a LEM to maintain an orbit around the moon at less than a free orbital speed…)
So I am contending that acceleration M, the additional amount of outward radial acceleration needed to keep P2 on earth’s orbital trajectory at the slower speed is: V^2/R – (V-S)^2/R
So where does M come from…? EARTH! Earth’s gravity G is way more than enough to keep P2 stuck to earth and keep traveling on earth’s orbital trajectory.
Particle P2 therefore weighes less by the amount:
(V^2/R -(V-S)^2/R) which I calculated to be approximately .0002M/sec^2
P3 is going faster so it’s velocity is (V+S) so you add M in the other direction … ETC.
No moon at all, two opposite acting amounts of differential acceleration at noon and midnight by the amount .0002M/sec^2 and, of course, S is the tangential velocity of a rotating earth’s equator WRT earth’s center.
There ain’t no such thing as a centrifugal or a centripetal force. There is only one relevant force, gravity, which accelerates the earth or moon, or any other planet, towards its primary. But as Newton’s Law (Which?) says that if a thing is moving it keeps on going in a straight line at the same speed UNLESS an external force acts on it, the earth (other planet, satellite, etc) moves subject to the result of momentum and acceleration roughly at right angles to the current direction of motion. Hence, the path is bent, result an ellipse.
Because of the size of the earth, the force of gravity is different on the side of the earth nearest to the sun to that on the side away. Hence, unless otherwise constrained, the two sides would then follow different orbits. But the two sides are constrained by the earth’s own attraction, and hence the earth does not fly apart. Still, it does its best, and the shell distorts, more so in the case of water which is more mobile, less in the case of the rocky portion. Hence tides and two bulges. Or, more properly, two bulges and, because of the earth’s rotation, two tides. QED.
Dudley Horscroft says: February 17, 2014 at 5:48 am “There ain’t no such thing as a centrifugal or a centripetal force. ”
Rubbish. HOW does anything turn without centripetal force? Do explain….
Dudley Horscroft says: February 17, 2014 at 5:48 am “There ain’t no such thing as a centrifugal or a centripetal force. ”
Centripetal force is that acting PRECISELY at a right angle to the velocity of a particle at all times hence – gravity on an object in orbit… always at a right angle … no change to the particle’s speed … only to it’s DIRECTION.
eyesonu,
“If I tied a brick to a rope and spun it around my head it would produce an outward force (centrifugal force) that would need to be countered acted by the rope. If we relate that concept of the orbiting brick and rope to a planet (brick) and gravitational attraction (rope) and call it a tidal force then would it be fair to say that the tidal force is the net result of gravitational attraction combined with the centrifugal force all wrapped into one package?”
You are confusing reference frames. From your point of view, spinning the brick, there is only one force which is the tension that you impart to the rope. This is called a centripetal force (centre directed) and it produces a centripetal acceleration (Newton’s second law). There is no balance of forces since this is a dynamic and not a static system. The concept of a centrifugal force (centre fleeing) arises when you place your point of view on the brick. Here you experience a “weight” directed outwards and to explain this, ie to make Newton’s second law work in this accelerating system, you have to invent a fictitious centrifugal force. You can’t have both the centripetal and centrifugal force at the same time. Compare this to the sensation of weight which is not the sensation of gravity which you can not feel, tidal effects aside, but the sensation of the normal force of the ground pushing you upwards. This is why centrifugal forces are not needed to explain the tidal effect since most explanations are done in a reference frame where they do not exist.
Willis,
I can’t seem to get a rise out of you. I guess that I’m just not trying hard enough. 😉
William Sears says: February 17, 2014 at 6:24 am “There is no balance of forces since this is a dynamic and not a static system. The concept of a centrifugal force (centre fleeing) arises when you place your point of view on the brick.”
A car is going around in a right hand circle. The centripetal force is supplied by the road surface sideways against the tires. The force is transmitted by structure to the left door which pushes on you centripetally to change your direction along with the rest of the car.
You ARE being pushed against the door by “centrifugal” force in the opposite direction of the centripetal force … as an inertial reaction to the centripetal force. This is no different than the force of the floor holding you up to counter the force gravity is imparting on you downwards. Two equal and opposite forces CANCELING OUT at the point of contact resulting in ZERO relative velocity between you and the floor. If you don’t think so – take way the floor. You begin accelerating down and … earth begins accelerating up.
Mike M,
“You ARE being pushed against the door by “centrifugal” force in the opposite direction of the centripetal force … as an inertial reaction to the centripetal force.” The door is pushing against you in order to impart the same centripetal acceleration that the roadway is imparting to the tires. It is only a centrifugal force in the non-inertial (accelerated) frame that you view as reality inside the car. The only force that you feel is the reaction (normal) force of the door or seatbelt. Centripetal versus centrifugal can be viewed as third law reaction forces but they apply to different objects in different reference frames.
You have misinterpreted my gravity – normal force statements which was a reference to the fact that in free fall you can not feel your own weight, an insight of Einstein. The same thing would apply to electrostatic attraction. Contact (normal, reaction or whatever term you prefer) forces are what you directly experience. Again tidal or tidal-like forces on an extended object are another question.
RichardLH says:
February 17, 2014 at 2:15 am
Why? It’s been referenced four times, and it says exactly what I said in the head post … was your citation somehow inadequate, such that it needed my assistance?
In any case, while that link is quite accurate, I found it much less complete than the reference yirgach gave and that I cited above … so sue me.
w.
Willis Eschenbach says:
February 17, 2014 at 10:00 am
“Why? It’s been referenced four times, and it says exactly what I said in the head post … was your citation somehow inadequate, such that it needed my assistance?”
Obviously not.
“In any case, while that link is quite accurate, I found it much less complete than the reference yirgach gave and that I cited above … so sue me.”
Down boy.
William Sears says:
February 17, 2014 at 6:24 am
Your problem is that you are far too reasonable, and your science-fu is strong, and you haven’t attacked me personally, or called me an idiot for not agreeing with you …
w.
I’ve known the Simanek page for some time and learning of it was a real eye opener.
Sorry if the following question is a needless distraction at this point in the discussion. Isn’t it so that a planet in orbit is following a straight path in (curved) spacetime? Do we actually still speak of gravity as a force then? Or is it just another imaginary force like the centrifugal force?
Thanks, Remmitt.
RichardLH says:
February 17, 2014 at 10:01 am
Richard, you address me using words that people use to address a dog … and then you act all surprised and shocked, and you clutch your pearls and bitch and whine when I stand up for myself and I don’t take your insults lying down.
You would be funny, if you weren’t so damn pathetic. Please, before you start on another of your hilarious rants about how reasonable and calm and pleasant you are, go stand in front of the mirror and look up “passive-aggressive” in the dictionary.
w.
remmitt says:
February 17, 2014 at 10:31 am
Do we actually still speak of gravity as a force then? Or is it just another imaginary force like the centrifugal force?
In science we have the concept of an ‘effective’ theory. That is a theory that gives the correct answer within its domain of validity or application. Treating gravity as a force works very well for calculating the position of the planets and guiding spacecraft to land where we want them to land, so is ‘effective’.
Willis Eschenbach says:
February 17, 2014 at 10:33 am
“Richard, you address me using words that people use to address a dog … and then you act all surprised and shocked, and you clutch your pearls and bitch and whine when I stand up for myself and I don’t take your insults lying down.”
I am sorry that I stooped to your level. It is just that you have consistently and frequently called me names and other such things.
“You would be funny, if you weren’t so damn pathetic. Please, before you start on another of your hilarious rants about how reasonable and calm and pleasant you are, go stand in front of the mirror and look up “passive-aggressive” in the dictionary.”
This from a rock(et) scientist who will plot dT on a graph and then not understand the meaning of the word delta or that ID vectors are what you use to create the x/y graph in the first place. Get a mirror for yourself.
Remmitt,
The orbital path is not a straight line in curved space time although it is the path of least action given the planet’s angular momentum and the central force it is subject to. It is sometimes suggested that gravity is a fictitious force (imaginary is not the usual word). See the following.
http://en.wikipedia.org/wiki/Fictitious_force#Gravity_as_a_fictitious_force
Willis,
I guess that I’m never so certain of myself to risk calling someone else an idiot, at least not in print. Maybe I could use a pseudonym. How does Scotian sound? In general though, I think that one should be more polite in print than face to face, not less.
I’m impressed by your boundless energy and it staggers me just to see it.
I have spent three days on trying to fully understand the discussions pertaining to this thread and I may have it figured out now but need a little time to express it. I hope those with a full understanding will monitor this thread closely another day or two.
I gotta get this issue resolved in my mind.
Willis, where have you lead me? LOL
I got it. Well I may not have “it” but I got something. Was your simple diagram meant to be the passage between a small chamber and a really really big one?
I hope to try to put into words the way a simple mind as mine sorted this out. But then I could be wrong and my mind simply way out in space. Anyway, the dogs need to be fed now.
Short post, yes. Mental focus, not so short.
Thank you, Willis for your response.
Thanks, Kevin. As you will note in Figure 1 and Figure 2, the tidal effects do not depend in any sense on centrifugal acceleration. There is no centrifugal acceleration in the Figures, the masses and the planet are falling straight into the sun … and yet we still have tidal forces.
So any explanation that depends on centrifugal acceleration is incorrect.
I don’t want to belabor the point, but I would then ask how is it that the Earth can accelerate continuously toward the sun or Moon without ever reaching them? Answer: The acceleration is centripetal, with the bodies in orbit around their common center of mass. If you pretend the Earth is an inertial system, then you are obliged to do something with the centripetal acceleration from the orbit on the “ma” side of Newton’s 2nd Law. It goes on over to the other side (among the “Fs”) and is a “centrifugal force”. Not a real force, but perfectly useful for calculations. I’m not arguing with the correctness of your model; I’m arguing that there are alternative views of the situation that aren’t necessarily wrong but actually quite useful. For example, if you use include this centrifugal psueodoforce as part of the gravitational potential, then you can explain the relative extrema in potential that are the various Lagrange points (L1 to L5) in the Earth Moon System; and the stability of those. Doing it in other ways is more complicated.
When lsvalgaard says the orbit has nothing to do with the tidal effect, I might point out that lunar cycle and lunar semi-cycle tides illustrate the pertinence of the orbit to the longer period tides. The tides are dynamical (not static equilibrium) and all the dynamics of Earth-Moon-Sun have to be accounted for.
Willis:
From this rather lengthy and detailed look at the Earth Tide which is a non-trivial part of this whole picture.
http://www.gps.caltech.edu/classes/ge167/file/agnew_treat_tide.pdf
“The Diurnal tidal potential (once per day) is largest at mid-latitudes and vanishes at the Equator and the Poles.
The Semi-diurnal part (twice per day) is largest at the Equator and vanishes at the Poles.
The Long-period tide is largest at the pole and (with reversed sign) at the equator.”
So your simple explanation only covers one small part of the overall picture, i.e. the Semi-diurnal part.
And this
http://www.whoi.edu/cms/files/lecture01_21351.pdf
for some calculations for working out the above. Including the rather important
Figure 7: Cotidal map.
Don’t know why the first link did not work – here is the full Google url for it
http://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&cad=rja&ved=0CD4QFjAC&url=http%3A%2F%2Fwww.gps.caltech.edu%2Fclasses%2Fge167%2Ffile%2Fagnew_treat_tide.pdf&ei=L5YCU-j-C8Gv7AaJi4GgBg&usg=AFQjCNEqnt-ey0dfZpC_Zbc0Uw6Ekt86bA&sig2=H1xV2WbBW8Y_qV–gOtxAQ
Having a bad day with Google urls
Link 2.
http://www.google.co.uk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=5&cad=rja&ved=0CFYQFjAE&url=http%3A%2F%2Fwww.gps.caltech.edu%2Fclasses%2Fge167%2Ffile%2Fagnew_treat_tide.pdf&ei=TpoCU_7bO8aQ7AaT1YHYCg&usg=AFQjCNEqnt-ey0dfZpC_Zbc0Uw6Ekt86bA&sig2=gTcccu9JbbBKJHEktqSASA
Kevin Kilty says:
February 17, 2014 at 2:51 pm
I don’t want to belabor the point, but I would then ask how is it that the Earth can accelerate continuously toward the sun or Moon without ever reaching them? Answer: The acceleration is centripetal, with the bodies in orbit around their common center of mass. If you pretend the Earth is an inertial system…
Perhaps the simplest explanation [without invoking centripetal acceleration] is how a satellite [or a cannonball] stays in orbit around the earth: http://www.physicsclassroom.com/mmedia/vectors/sat.cfm
RichardLH, can be frustrating can’t it. Stripped this out of your huge Google link. You have to find the actual url buried within the google’s link and use a paste to a text editor to dig for it. Here it is:
http://www.gps.caltech.edu/classes/ge167/file/agnew_treat_tide.pdf
wayne says:
February 17, 2014 at 4:46 pm
RichardLH, can be frustrating can’t it. Stripped this out of your huge Google link. You have to find the actual url buried within the google’s link and use a paste to a text editor to dig for it.
As I did for everybody in my post upthread:
lsvalgaard says:
February 16, 2014 at 10:00 pm
…A full [but lengthy] treatment is here http://www.gps.caltech.edu/classes/ge167/file/agnew_treat_tide.pdf
I see another “tide” quandry has broken out. A couple of points. (that may already be made in other comments):
There is no real centrifugal force. It is only gravity that matters to tides.
The “far side” does have a NET vector away from the planet, so it is reasonable to say the “Net Tide Raising Force” is opposite in direction on the two sides. The real gravity force is always one way though, and it is the ‘lessening with distance’ that leads to the net force having opposite directions on the vectors.
Would be a reasonable statement if they said “Net tide raising force”…
See the pictures here:
https://chiefio.wordpress.com/2014/02/16/tides-vectors-scalars-arctic-flushing-and-resonance/
Also has a nice link to a page that specifically addresses wrong ways to think about tides and bad examples from text books:
http://www.lhup.edu/~dsimanek/scenario/tides.htm
One other minor point: Since the moon orbits the sun, us not so much, it is not like other moons that neatly circle in the equatorial plane. It is tilted about 5 degrees to the ecliptic, and our equator is tilted about 23.5 degrees. So once a year the moon goes from a lunar monthly 23.5+5 = 28.5 to a 23.5 -5 = 18.5 degree excursion. That means it is bouncing “up and down”. As the lunar orbit precesses, just which season that more / less tides land in which hemisphere changes. So you really do have to allow for variations in the orbit changing where the gravity vector points, and how strong it is. It doesn’t just to around with a tidal bulge at the equator. That bulge wanders north / south too, and has a 9 and 18 year set of periods to how it aligns with the seasons / hemispheres and a 3 x that or about 56 year re-sync with exactly the same patches of dirt under it. As the reflections off of continents can be bigger than the actual tide directly raised, “this matters”. Rather a lot. It drives current formation and changes, and the degree and location of tidal mixing of deeper cool water to the surface. Periodically…
lsvalgaard says:
February 17, 2014 at 4:52 pm
As I did for everybody in my post upthread:
—
Missed that Leif, should have researched the thread to see if that embedded url already exited and that seems a paper well worth reading, thanks, pointed twice might get more to notice it if they missed your link on their pass through. Happened to me, time’s limited and can’t read every single thing.
wayne says:
February 17, 2014 at 5:17 pm
Happened to me, time’s limited and can’t read every single thing.Saying it again and again may make more people read it, so is not a bad thing. Unfortunately, geniuses like bart will not even try.
RichardLH says:
February 16, 2014 at 2:03 pm
“…or did I get something wrong?”
Who cares? Centripetal acceleration from Earth spin is the same everywhere at the surface and radially symmetric with respect to the center of the Earth. It has no net effect. Centripetal acceleration due to movement about the Sun is greater on the far side, and weaker on the near side. That is the kind of stress inducing delta-acceleration which causes tidal bulges.
lsvalgaard says:
February 16, 2014 at 10:00 pm
I’m sorry that you cannot understand the math, and must try to find references to back you up without apparently being able to argue on your own. I’ve given the very simple and obvious equations above.
Willis Eschenbach says:
February 17, 2014 at 12:25 am
“Got it … so, can we assume that your method is from the ultra-new field of investigation called “Science By Assertion”?”
What a load of crap. How many times have I posted here explaining things? I gave you the equations right up above. You havn’t done the math at all.
“The Earth is in free fall towards the Moon, attracted by the gravitational force.”
No! The Earth center is in free-fall towards the Moon. The rest of the Earth is being pulled along for the ride. Only the very center is in free fall. The fact that the rest of the Earth is being pulled differntly than the center is the very thing that causes the tidal bulges.
lsvalgaard says:
February 17, 2014 at 5:47 pm
Do the math, Leif. Can you?
………………Thanks, Leif, fixed. It’s micronewtons ………………….
Willis, are you absolutely sure that it is micronewtons? Could you express it in milligee? I think that it is around 3.1 x 10-3 g. We actually measure this with extremely sensitive accelerometers.
In Low Earth orbit the number is about 1 x 10-7 g per meter. Yes, I have measured this term and this is why the most stable orientation of the space shuttle 18.5 meters long, was nose down or nose up vertical…
Mike M says: February 17, 2014 at 6:42 am
“You ARE being pushed against the door by “centrifugal” force in the opposite direction of the centripetal force … as an inertial reaction to the centripetal force. The door is pushing against you in order to impart the same centripetal acceleration that the roadway is imparting to the tires.”
William Sears says: February 17, 2014 at 7:29 am “It is only a centrifugal force in the non-inertial (accelerated) frame that you view as reality inside the car. ”
I disagree. The reality inside the car is that when you open the door, BOTH the centripetal force that was causing you travel in a circle – AND – your inertial reaction to it, centrifugal force of you pushing against the door, … disappear.
My consternation over the use of “centrifugal force” is ONLY when it is used to describe what happens when there is no door (and no friction between you and the seat), and you go flying out of the car when it turns. Many people would say “centrifugal force” “pushed” you out of the car and that is indeed a thoroughly fictitious concept – it was the car that slid out from under you.
Bart says:
February 17, 2014 at 9:48 pm
Do the math, Leif. Can you?
Obviously, but why bother? the links I gave you to study [have you?] should be enough.
denniswingo says: February 17, 2014 at 10:03 pm “Willis, are you absolutely sure that it is micronewtons? Could you express it in milligee? I think that it is around 3.1 x 10-3 g. We actually measure this with extremely sensitive accelerometers.”
Are you saying that you measure that much of a reduction of gravity occurring (maximally) at noon and midnight? If so, could you please verify the magnitude because I calculated .0002 meter/sec^2 (.00002 g) earlier on by another effect.
lsvalgaard says:
February 17, 2014 at 10:11 pm
Come on Leif. Put up or shut up. Which of these equations is wrong, and why?
denniswingo – I forgot to ask, at what latitude are the accelerometer measuring that?
Bart says:
February 17, 2014 at 10:27 pm
Come on Leif. Put up or shut up.
Elementary, dear Watson. The correct derivation goes like this:
a = distance to Sun; r = radius of Earth; M = solar mass; difference between gravitational force on small mass m on either side of the Earth dF = GMm/a^2((1+r/d)^(-2) – (1-r/a)^(-2)) = -4GMm r/a^3 (for r much smaller than a).
lsvalgaard says:
February 17, 2014 at 10:48 pm
Not an answer to the question posed. And, wrong. You have neglected the centripetal acceleration with respect to the Sun.
We are talking about a circular orbit here, and to make things simple, we are talking about a tidally locked body.
What is the centripetal acceleration with respect to the Sun of the sub-solar point on the near side?
What is it on the far side?
Are they the same? Why or why not?
Don’t weasel your way out of it. Answer the questions.
Don’t give me any guff that I am making the tidal bulge go away when there is no orbit, and the body is falling straight toward the Sun. The accelerations are still there, just 33% less.
Don’t make the specious claim that the body, the Earth in this case, is in free-fall. As I explained above, only the center of the Earth is in free-fall.
Now, tell us exactly why the laws of physics do not hold for Earth tides. Or, man up and admit that I am, and have been, right.
I am waiting…
Bart says:
February 17, 2014 at 10:56 pm
Not an answer to the question posed. And, wrong. You have neglected the centripetal acceleration with respect to the Sun.
Your question was ill-posed to begin with [i.e. not even wrong]. For the Earth, the ‘orbital’ acceleration is the acceleration caused by the Sun at the center of the Earth. Instead of me making my own drawing, I will refer you to Figure 2 of http://www.gps.caltech.edu/classes/ge167/file/agnew_treat_tide.pdf
(substitute Moon with Sun for the Sun case).
lsvalgaard says:
February 17, 2014 at 11:15 pm
“For the Earth, the ‘orbital’ acceleration is the acceleration caused by the Sun at the center of the Earth.”
LOL. So, it is the same at the sub-solar point and its antipode? Please explain to us how the orbital tracks around the Sun at D-r and D+r radii are precisely the same circumference. This should be good…
Really, Leif. When you find yourself in a hole, stop digging. Man up, and admit you are wrong.
Bart says:
February 17, 2014 at 11:27 pm
LOL. So, it is the same at the sub-solar point and its antipode? Please explain to us how the orbital tracks around the Sun at D-r and D+r radii are precisely the same circumference.
The easiest would be for you to actually read from the paper . Start with section 3.06.2.1 and learn about the tidal forces.
Anticipating a lame response, in so many words:
“But, gravity is magical. It cancels the centripetal acceleration at both D-r and D+r, as well as at D.”
No. If it did, then the point at D-r would have to be moving at orbital rate omega = sqrt(mu/(D-r)^3), and the point at D+r would have to be moving at orbital rate omega = sqrt(mu/(D+r)^3). And, if that happened, the Earth would quickly tear itself apart.
The Earth center is pulling everything along at omega = sqrt(mu/D^3). The point at D-r is fighting being pulled along at that rate, both by the gravity at D-r which is stronger, and the centripetal acceleration at D-r, which is weaker. Mutatis mutandis at D+r.
Both effects influence the tides.
lsvalgaard says:
February 17, 2014 at 11:31 pm
“The easiest would be for you to actually read from the paper.”
No, the easiest thing for you is to defend your point of view, or admit that you do not understand the math, and must allow others to make your point for you.
But, then, that would also be an admission that you do not understand what they have written, and are taking it on faith that A) they did it right and B) you are sure they agree with you.
Bart says:
February 17, 2014 at 11:38 pm
No, the easiest thing for you is to defend your point of view
My point of view is based on what generations of scientists have pondered for centuries. Our modern treatment of tidal theory is based on the work by Munk and Cartwright (1966) and I happen to agree with them (understanding what they said): http://www.leif.org/EOS/Munk-Tides-1966.pdf You should study their work and learn something. Especially their derivation of the tidal potential starting on page 538, equation (2.4). Tell us where they go wrong in your opinion.
lsvalgaard says:
February 17, 2014 at 11:49 pm
If you cannot defend your POV, then you do not understand it.
Bart says:
February 17, 2014 at 11:53 pm
If you cannot defend your POV, then you do not understand it.
Nonsense. I think Maxwell’s equations, Newton’s law, etc are valid and that I understand them and can use them. I do not have to defend what they said beyond what they themselves did. But, in any event, a physical understanding can be got in the tide-problem by remarking that the equations are the same whether you assume the Earth going around the Sun or the Sun going around the Earth [in an otherwise empty Universe].
lsvalgaard says:
February 18, 2014 at 12:02 am
Nonsense. You haven’t the faintest idea of what to do with the centripetal acceleration terms.
Here’s a clue for you Leif: the effect is to amplify the accelerations by a factor of 3/2. They retain the same form otherwise, so can even be lumped in as scaling of the potential. And, since the papers you cite are looking for functions proportional to the equipotential surface, they have absolutely nothing to say on this score.
I showed you how the factor of 3/2 emerges in the calculation of the Roche Limit at the end of this section. Look at the equations:
See how the factor of 2 becomes a factor of 3? It’s right there.
You’re wrong, and you’re only arguing with me because we don’t like each other. Give it up. You’re hurting yourself more than me.
Bart says:
February 18, 2014 at 12:13 am
I showed you how the factor of 3/2 emerges in the calculation of the Roche Limit…
That was the rotation of the body itself, not orbital motion.Read Appendix A of http://www.leif.org/EOS/Munk-Tides-1966.pdf and learn.
You’re wrong, and you’re only arguing with me because we don’t like each other
That may be your motivation, mine is to educate you.
Some interesting facts about tides (the short version)
The Earth is an oblate spheriod.
The Earth’s equatorial radius is the distance from its center to the Equator and equals 6,378.14 kilometers
The Earth’s polar radius is the distance from its center to the North and South Poles and equals 6,356.75 kilometers
A 21.39 kilometers difference.
Angular velocity of Earth’s axial rotation in radians per second = 7.29 x 10^-5 rad/s
Angular velocity of Earth around the Sun in radians per second = 1.99 × 10^-7 rad/s
Centripetal (outwards) acceleration at Earth’s surface due to Earth’s axial rotation = 0.034 m/s^2
Centripetal (outwards) acceleration at Earth’s surface due to Earth’s orbit around the Sun ~ 0.0000952 m/s^2
Gravity at Earth’s surface = 9.8 m/s^2
The tiny differential between 9.8 m/s^2 (Polar) and 9.834 m/s^2 (Equatorial) creates the 21.38 kilometers difference in radii above.
The Oceans average depth is 3.79 kilometers so 3.79 / (6,378.14 – 3.79) =~ 1 / 1682 so the difference is mostly in the rock.
The Solar tidal force is 46% as large as the Lunar. More precisely, the Lunar tidal acceleration (along the Moon–Earth axis, at the Earth’s surface) is about 1.1 * 10^-7 * 9.8 m/s^2,
while the Solar tidal acceleration (along the Sun–Earth axis, at the Earth’s surface) is about 0.52 * 10^-7 * 9.8 m/s^2.
The theoretical amplitude of Oceanic tides caused by the moon is about 54 centimetres at the highest point, which corresponds to the amplitude that would be reached if the Ocean possessed a uniform depth, there were no landmasses, and the Earth were rotating in step with the Moon’s orbit. The Sun similarly causes tides, of which the theoretical amplitude is about 25 centimetres (46% of that of the Moon) with a cycle time of 12 hours. At Spring tide the two effects add to each other to a theoretical level of 79 centimetres, while at Neap tide the theoretical level is reduced to 29 centimetres. Since the orbits of the Earth about the Sun, and the Moon about the Earth, are elliptical, tidal amplitudes change somewhat as a result of the varying Earth–Sun and Earth–Moon distances. This causes a variation in the tidal force and theoretical amplitude of about ±18% for the moon and ±5% for the sun. If both the Sun and Moon were at their closest positions and aligned at New Moon, the theoretical amplitude would reach 93 centimetres.
Real amplitudes differ considerably, not only because of depth variations and continental obstacles, but also because wave propagation across the ocean has a natural period of the same order of magnitude as the rotation period: if there were no land masses, it would take about 30 hours for a long wavelength surface wave to propagate along the equator halfway around the Earth (by comparison, the Earth’s lithosphere has a natural period of about 57 minutes). Earth tides, which raise and lower the bottom of the ocean by less than 1 metre,and the tide’s own gravitational self attraction are both significant and further complicate the ocean’s response to tidal forces.
In most locations, the four largest amplitude tidal components turn out to be:
M2 Principal lunar 12.42 hr
K1 Luni-solar diurnal 23.93 hr
S2 Principal solar 12.00 hr
O1 Principal lunar diurnal 25.82 hr
S2 is largest at mid-latitudes and vanishes at the Equator and the Poles.
M2 is largest at the Equator and vanishes at the Poles.
The Long-period tide (not listed above) is largest at the pole and (with reversed sign) at the equator.
A list of other components can be found in Knauss (1978) table 10.1. Particularly important is the fortnightly (2 week) tide, often written Mf.
See Figure 10.15 in Knauss (1978) for plots of partial tides.
Tides in different locations are classified based on the predominant frequency of the tide using a function called the form ratio which measures the relative strength of the diurnal and semi-diurnal tides.
F = (K1 + O1) / (M2 + S2)
F > 3 Diurnal 1 High, 1 Low per day
0.25 < F < 3 Mixed 2 Highs, 2 Lows per day, but of different strength
F < 0.25 Semidiurnal 2 Highs, 2 Lows per day, similar strength.
Bart says:
February 17, 2014 at 9:48 pm
“Who cares? Centripetal acceleration from Earth spin is the same everywhere at the surface and radially symmetric with respect to the center of the Earth. It has no net effect. Centripetal acceleration due to movement about the Sun is greater on the far side, and weaker on the near side. That is the kind of stress inducing delta-acceleration which causes tidal bulges.”
Because it you take the Earth’s rotation value you can add and subtract the Earth orbital value to get the difference Sun side to Dark side?
0.034 m/s^2 ± ~0.0000952 m/s^2
which is what I thought you were discussing.
wayne says:
February 17, 2014 at 4:46 pm
“RichardLH, can be frustrating can’t it. Stripped this out of your huge Google link. You have to find the actual url buried within the google’s link and use a paste to a text editor to dig for it. Here it is:
http://www.gps.caltech.edu/classes/ge167/file/agnew_treat_tide.pdf”
Even more frustrating is that the shortcut you have and the shortcut I have are apparently the same (copied to Notepad) but yours works and mine doesn’t!
lsvalgaard says:
February 18, 2014 at 12:18 am
“That was the rotation of the body itself, not orbital motion.”
The body is orbiting at synchronous rate, i.e., with the orbital motion. The effect can thus be attributed either way – to rotation or to orbital motion. If you really want to separate the two, you need to tilt the axis of rotation away from the orbit normal.
In any case, the fact remains that the differential acceleration from the sub-solar point to the antipode is 6*(mu/D^3)*r, and not 4 times. This clearly has an effect on the Roche limit, and my equations are correct.
Bart says:
February 17, 2014 at 9:48 pm
Or were you talking about
Angular velocity of Earth’s axial rotation in radians per second = 7.29 x 10^-5 rad/s
Angular velocity of Earth around the Sun in radians per second = 1.99 × 10^-7 rad/s
and
Earth’s average orbit of 149.59787 * 10^6 kilometres
and Earth’s equatorial radius of 6,378.14 kilometres
Having read the links provided it seems to me that we are dealing with tidal predictions now which is not the same thing as asking why there are tides at any given point in time on a specific place on the earth.The word potential I think would best describe the effect of all the forces acting on the earth,moon and the sun etc. which determines there exact position and tidal forces in the future rather than imaginary.My simple understanding is.
http://en.wikipedia.org/wiki/Tide
Bart says:
February 18, 2014 at 3:07 am
The body is orbiting at synchronous rate, i.e., with the orbital motion.
Is an irrelevant straw man, only used to give an example of a possible rotation rate.
don penman says:
February 18, 2014 at 3:42 am
“My simple understanding is. http://en.wikipedia.org/wiki/Tide”
Totally correct. The rather limited view that a single vector treatment of the rather more complex true nature of tides can be seen from the M2 tidal plot in that link alone. That shows just how complex this all is in reality. Even if you understand correctly the top 4 ways in which the field changes, the way the Earth reacts to them is hardly recognisable from even that slightly more complex viewpoint.
Mike M,
“I disagree. The reality inside the car is that when you open the door, BOTH the centripetal force that was causing you travel in a circle – AND – your inertial reaction to it, centrifugal force of you pushing against the door, … disappear.”
“My consternation over the use of “centrifugal force” is ONLY when it is used to describe what happens when there is no door (and no friction between you and the seat), and you go flying out of the car when it turns. Many people would say “centrifugal force” “pushed” you out of the car and that is indeed a thoroughly fictitious concept – it was the car that slid out from under you.”
You have to keep in mind that the centripetal and centrifugal forces that you refer to do not exist together but are used to describe the situation in different reference frames. In the inertial frame the centripetal force disappears when you lose contact with the door as the reaction force of the door pushing on you is gone and you then travel in a straight line as per Newton’s first law. In the non-inertial (rotating) frame the centrifugal force does not disappear as it is not caused by the reaction force of the door but was balanced by it, thus producing the static situation as seen inside the car. Remove the door and the centrifugal force then causes the person to leave the car. The statements that the centrifugal force pushed you out of the car versus the car slid away from you are not contradictory. They are just the different views of the two reference frames.
I am not sure what you mean by “inertial reaction”. You clearly wish to view things from the inertial frame and there is nothing wrong with this but at the same time you wish to retain the term centrifugal. This is a problem. Non-inertial frames are used because in many situations they greatly simplify the mathematics and make it easier to interpret results. Try to explain what is going on when a bug crawls around on a horizontal non-uniformly rotating disk without them. For that matter try explaining the motion of the earth’s atmosphere or oceans on a global scale in an inertial frame of reference. You have to get the details right.
Bart says: February 17, 2014 at 9:48 pm ” Who cares? Centripetal acceleration from Earth spin is the same everywhere at the surface and radially symmetric with respect to the center of the Earth.”
This is exactly why I stole earth’s rotation away from ‘them’ with my free body model above (February 17, 2014 at 5:25 am). It allowed me to demostrate that an additional force is needed to keep a particle on earth’s orbital path IF it is going slower than earth’s free orbital speed. (One of ‘them’ actually stated that staying on earth’s orbital radius at some other speed than earth’s free orbital speed was “impossible” – which is pure BUNK!) In this slower case, that ~other~ force must act away from the sun to counter sun’s gravity to thereby decrease the centripetal force down to the reduced amount needed to keep the particle traveling on earth’s free orbital path at the slower speed. If the velocity dropped to zero, that amount of extra thrust needed would become EXACTLY – the force of sun’s gravity on the particle and the particle would simply hover above the sun at a altitude from the sun equal to earth’s orbital radius.
And, for any instant in time, it could be a long rope to Jupiter, it could be a rocket thruster or it could be … a weenie bit taken away from the inertial reaction to earth’s gravity – which would indeed register on a very sensitive bathroom scale or accelerometer.
Conversely, when a particle is going faster than free orbital speed, again some ~other~ force, but this time acting toward the sun, is required to keep it on earth’s free orbital path. It could go 10, 100, 1000 times earth’s velocity and yet stay on earth’s orbital path, it would just require a lot more of thrust to produce the required centripetal force over that provided by sun’s gravity.
Bart, you and I are of course speaking of exactly the same effect, one with net force differentials acting in the same direction as Willis’ effect but, (as I believe to be), a ~couple orders of magnitude stronger than his.
I suspect that we are getting nowhere here because we are bucking … the consensus.
(It’s why my eyes lit up when I saw denniswingo’s comment, February 17, 2014 at 10:03 pm, because there may empirical evidence to back us up. Hope he returns with more details… )
Ohh, how much simpler it would be to explain the gravitational effects with a series of simple diagrams. It could be relatively easy to explain how an orbit of one body around another could come to be. Use of only gravitational force and inertia.
A picture is worth a thousands words.
For those having a hard time with this discussion on this thread, get a few big rocks and go off into deep space and play around with them (in your mind only of course). From Willlis’ simple diagram you can find the source/direction of gravitational forces far far away.
I hope to find time to put it all in words but the mortgage company is not interested my educational endeavors.
William Sears says: “I am not sure what you mean by “inertial reaction”.
We’ve already been over this. Gravity is pulling you down and the inertial reactive force is the ground pushing you up – equal and opposite. Take the latter one away and down you go!
How about I construct a trap door over a vertical mine shaft, have you stand on it and then you scream to me about non-inertial reference frames after I pull the lever?
If you are on rusty roller skates and I’m pushing 50 pounds against you to keep you moving at 2 feet/sec I feel that same 50 pounds, as a reaction, pushing BACK on me thus I am doing REAL work = F*V REAL heat comes from your rusty roller skate bearings in ANY frame of reference.
Mike M:
Earth’s average orbit = 149,597,870.00 kilometres
Earth’s equatorial radius = 6,378.14 kilometres
Remind me again about how much difference this makes as to the forces involved.
RichardLH says: February 18, 2014 at 8:50 am
Earth’s average orbit = 149,597,870.00 kilometres
Earth’s equatorial radius = 6,378.14 kilometres
Remind me again about how much difference this makes as to the forces involved.
************************
I said February 15, 2014 at 7:13 am
A quick look gave me a result for a “no moon” variation of “midnight fling” acceleration over average center V^2/R of 3%. For now I’d say it looks significant.
Earth’s average orbit velocity V1 as 29885 m/sec. Crust WRT center V2 as 463 m/sec. So combined velocity in orbit around the sun at midnight V1+V2=V3 as 30349 m/sec V3^2 / V1^2 = 1.03
****************************
I don’t have the other numbers in front me at my current location but as stated above, the difference in earth orbit centripetal acceleration was about 3% which yielded an acceleration difference of .00018 M/sec^s at noon and midnight on the equator.
(Bart did it with rotational vectors and I did it with velocities – same concept.)
I just now realized that how I earlier described how this effect drops off as you move from the equator toward either pole was in error. I think I stated per cosine(latitude) but now see it drops off per [cosine(latitude)]^2 where Willis’ effect drops off more gradually as cosine(latitude).
lsvalgaard says:
February 18, 2014 at 3:44 am
“Is an irrelevant straw man, only used to give an example of a possible rotation rate.”
It can hardly be irrelevant when it’s the case I’ve been arguing.
Mike M. says:
February 18, 2014 at 8:22 am
We may be arguing along the same lines. Will have to review. More later.
Bart says:
February 18, 2014 at 9:51 am
“Is an irrelevant straw man, only used to give an example of a possible rotation rate.”
It can hardly be irrelevant when it’s the case I’ve been arguing.
You are laboring under the false assumption that your argument is relevant. Let me explain: If a rock pile [the moon approaching the planet] is rotating fast enough it will fly apart regardless of the tidal effects. If it does not rotate at all, then only the tidal effect plays a role. In the intermediate case both the tidal effect and the rotation work in concert to make the moon break up. Under the assumption that the rotation rate is that of a tidally locked moon [not a bad assumption], the rotational role of the breakup is to raise the factor from 2 to 3. This has nothing to do with the orbital centripetal acceleration in causing tides, and is thus irrelevant.
I am amazed that this thread broke out in full argument last night again. Mike M, Bart, and I have been arguing that there are alternative ways to look at the tides, and that the pseudoforces like “centrifugal” can be used in a consistent explanation. Willis has correctly explained the tides with his rope model, but seems insistent that other models making use of centrifugal force are just plainly wrong. Edwin Smith has stated that “gravity” is the entire story to the tides. It is not. This would imply that the tides are a problem in engineering statics, but in fact they need an acceleration of some sort to complete the explanation. They are dynamical phenomena.
The tides do not just slosh across the ocean basins, but actually circulate around amphidromic points in the various ocean basins, and even in lakes. You see, the “coriolis force” another of the pseudoforces that arise from treating the Earth as an inertial frame, is important to the complete picture as well.
Willis, if I could make a suggestion that could become the basis of an interesting thread, numerous textbooks, popular science books, and even articles from Scientific American make the claim that enhanced tides in places like the Bay of Fundy, result from resonance. Not so. A far more correct explanation is available if one simply examines the shape that most estuaries and bays obtain. Are you game to tackle this?
Kevin Kilty says:
February 18, 2014 at 10:22 am
This would imply that the tides are a problem in engineering statics, but in fact they need an acceleration of some sort to complete the explanation. They are dynamical phenomena.
There seems to be some confusion about this. The ‘static’ part has to do with the tidal forcing, and the ‘dynamical’ part has to do with the response of the oceans to that forcing. This was understood and explained by Laplace way back in the middle of the 18th century and is thoroughly discussed in http://www.leif.org/EOS/Munk-Tides-1966.pdf
Mike M. says:
February 18, 2014 at 9:40 am
“I don’t have the other numbers in front me at my current location but as stated above, the difference in earth orbit centripetal acceleration was about 3% which yielded an acceleration difference of .00018 M/sec^s at noon and midnight on the equator.”
And that compares to
Angular velocity of Earth’s axial rotation in radians per second = 7.29 x 10^-5 rad/s
Angular velocity of Earth around the Sun in radians per second = 1.99 × 10^-7 rad/s
I am not sure how you got to that figure.
Remember the Earth rotates against the orbit on the near side. (looking from above as conventional).
That axial rotation just HAS to be the largest component in all this. Then you can add/subtract the two orbital components. You may be right in that the differential dark/light is bigger than the orbital but I am not sure that you are right, I think it is the other way round.
lsvalgaard says: February 18, 2014 at 9:59 am
If I was able to prove to you using a sensitive (and appropriately highly damped to take out fast seismic signals) accelerometer or other such apparatus that things weigh less at the equator by a factor of .00018 Newtons per Kg maximum at noon and midnight versus what they weigh at 6am and 6pm …
Would not such a measurement provide a valid reason for having two bulges at both noon and midnight and it’s magnitude exclude it’s existence being caused by the much smaller effect per WIllis?
In your link, http://www.gps.caltech.edu/classes/ge167/file/agnew_treat_tide.pdf on pub page 171, PDF page 9,
Doodson’s harmonic analysis clearly shows a fairly strong semidiurnal tide factor with a period of exactly 2.000000 that he associated with the sun. Something is causing it and part of that is WIllis’ effect but if measured to be a lot stronger then ~something else~ is much more responsible.
Mike M. says:
February 18, 2014 at 9:40 am
Centripetal (outwards) acceleration at Earth’s surface due to Earth’s axial rotation = 0.034 m/s^2
Centripetal (outwards) acceleration at Earth’s surface due to Earth’s orbit around the Sun ~ 0.0000952 m/s^2
How you get the tiny differential between orbit + radius and orbit – radius centred around orbital to be bigger than the orbital itself is a mystery to me.
Mike M. says:
February 18, 2014 at 10:35 am
Doodson’s harmonic analysis clearly shows a fairly strong semidiurnal tide factor with a period of exactly 2.000000 that he associated with the sun. Something is causing it and part of that is WIllis’ effect but if measured to be a lot stronger then ~something else~ is much more responsible.
Your question is sufficiently obscure that I’m not sure what you are hinting at. Perhaps our resident mathematical genius can interpret what you said and provide a compelling answer.
RichardLH says: February 18, 2014 at 10:33 am
“You may be right in that the differential dark/light is bigger than the orbital but I am not sure that you are right, I think it is the other way round.”
Bigger than orbital!?! I never stated anything of the sort. I stated: Earth’s average orbit velocity V1 as 29885 m/sec. Crust WRT center V2 as 463 m/sec. (WRT EARTH’S center)
Solar orbital velocity DIFFERENCE is 463m/sec (minus at noon, plus at midnight) – so either subtract it or add it to/from 29885 m/sec.
RichardLH says: February 18, 2014 at 10:40 am “Centripetal (outwards) acceleration at Earth’s surface ….” BLAH BLAH BLAH!!!!
This is the 2nd time I’ve told you that has NOTHING to do with this (and I think so has Bart).
I already took it away from you anyway! Go back and read my free body description February 17, 2014 at 5:25 am I describe the difference in the centripetal required for a particle traveling along earth’s orbital path at a slower or faster speed but WITHOUT any earth at all let alone a spinning one.
Stop bringing it up, it is TOTALLY non sequitur to the description.
Mike M. says:
February 18, 2014 at 10:56 am
So we have two particles – non rotating – in orbit around the Sun.
One at 149,597,870.00 + 6,378.14 kilometres
One at 149,597,870.00 – 6,378.14 kilometres
Centripetal (outwards) acceleration at Earth’s centre due to Earth’s orbit around the Sun ~ 0.0000952 m/s^2 at the mid point between them.
You really think that the tiny differences from that mid point for the far and the near particle given their differences in orbital values are significant?
When compared to G 9.8 m/s^2 (holding particles onto the surface) and that Centripetal (outwards) acceleration at Earth’s surface due to Earth’s axial rotation = 0.034 m/s^2
I tell you what – do the vector sums and come back with the figures. If they are anything other than up/down to Earth centre on almost any scale of graph you can construct…..
Dudley Horscroft says: February 16, 2014 at 8:33 pm “BTW, the earth and the moon do not rotate around each other, or around the barycentre. ”
Quick, tell NASA not to launch Apollo 8! … oh… too late ….
http://upload.wikimedia.org/wikipedia/commons/5/5c/Apollo-8-mission-profile.png
RichardLH says: February 18, 2014 at 11:32 am
So we have two particles – non rotating – in orbit around the Sun.
One at 149,597,870.00 + 6,378.14 kilometres
One at 149,597,870.00 – 6,378.14 kilometres
**********************
Wrong. They are BOTH at 149,597,870.00 km
Try again…
Mike M. says:
“We’ve already been over this. Gravity is pulling you down and the inertial reactive force is the ground pushing you up – equal and opposite. Take the latter one away and down you go!”
It would be helpful if you used standard names. Above you are referring to the normal force or reactive force. Using the vague term “inertial reaction” makes it very hard to know what you are talking about.
“How about I construct a trap door over a vertical mine shaft, have you stand on it and then you scream to me about non-inertial reference frames after I pull the lever?”
This sentence is absolutely devoid of meaning. The same phenomenon can be described in either inertial or non-inertial frames of reference. One or the other is chosen for mathematical convenience, but you can not mix the two as you seem to do.
“If you are on rusty roller skates and I’m pushing 50 pounds against you to keep you moving at 2 feet/sec I feel that same 50 pounds, as a reaction, pushing BACK on me thus I am doing REAL work = F*V REAL heat comes from your rusty roller skate bearings in ANY frame of reference.”
You are right, it does apply in all reference frames, although the method of approach will vary. As hard as I try I do not see what it is that you are getting at. By the way, please note that F*V is power not work.
I’m beginning to suspect that the problem is to be found in this quote from Wikipedia:
“Centrifugal force (from Latin centrum, meaning “center”, and fugere, meaning “to flee”[1][2]) is the apparent force that draws a rotating body away from the center of rotation. It is caused by the inertia of the body as the body’s path is continually redirected. In Newtonian mechanics, the term centrifugal force is used to refer to one of two distinct concepts: an inertial force (also called a “fictitious” force) observed in a non-inertial reference frame, and a reaction force corresponding to a centripetal force.”
You may be using the second definition when others are using the first, and more common, definition. I don’t think that this is the only problem though, as you do not seem to like non-inertial frames at all.
William Sears says: February 18, 2014 at 11:55 am ” You may be using the second definition when others are using the first, and more common, definition.”
Guess no longer, I am using the second one because it is the correct one and being “uncommon” is of no concern to someone like me.
William Sears:
I wrote, “I am doing REAL work” Being in the course of DOING work infers the expenditure of power. Sorry I wasn’t scientifically precise enough with the terminology to prevent you from using it for a cheap shot….
For folks frustrated by Google giant URLs: Don’t just “copy link” from a google search, click the link, then copy it from the browser bar. Or use a more polite search engine that doesn’t track tag and bag you, like this one: https://duckduckgo.com/?q=duckduckgo that does not feel compelled to drive you through their site with obscure URL tricks…
Mike M. says:
February 18, 2014 at 11:54 am
“Wrong. They are BOTH at 149,597,870.00 km”
So following each other in the same orbit?
Mike M,
Power vs Work: It wasn’t a cheap shot since there was nothing critical in what I said. I’m sorry that you took it that way.
“Guess no longer, I am using the second one because it is the correct one and being “uncommon” is of no concern to someone like me.” The correct one, really? You have to be able to communicate with other people and if the language is physics you have to know the terms. There was enough mention of fictitious forces and reference frames for you to understand the context. If all this was just a misunderstanding of terms then I expect that you will now withdraw your objections to my previous posts. Although I feel obliged to point out that the initial objection had to do with asteroids falling into the sun and there wasn’t any centrifugal force there, by either definition.
William Sears says: February 18, 2014 at 12:41 pm “There was enough mention of fictitious forces…”
I’m an engineer why should I give a rat’s rear end about “fictitious forces” when the real ones are plenty enough to keep me busy?
RichardLH says: February 18, 2014 at 12:27 pm “So following each other in the same orbit?”
Yeah… okay. It’s a circular orbit for the purpose of illustration so they can be on opposite sides of the sun for all I care.
lsvalgaard says: February 18, 2014 at 10:43 am “Perhaps our resident mathematical genius can interpret what you said and provide a compelling answer.”
Color me consigned to wait for such an eventuality. (My wife doesn’t understand me half the time either so I’m used to it.)
William Sears says: February 18, 2014 at 12:41 pm “I’m sorry that you took it that way. ”
Don’t be, I’m the one who was joking so I should be apologizing to you. Sorry.
We may be talking past one another here, but I don’t see that anyone on this thread denies that gravity is the “cause” (forcing) of the tides, but you, yourself, used the term “tidal effect” which suggests to me what we ultimately observe as the tides–i.e. things beyond the cause. There is no means of applying nothing more than gravity to explain what one observes of the tides. Willis included an acceleration of the three masses in his explanation, not just gravity, and as a linear acceleration, or as the centripetal acceleration in an orbit, these can be represented by a “fictitious force” (translational in the linear case, or centrifugal in the case of orbits). Every textbook I have ever consulted on dynamics, and I have taught the subject in both physics departments and in engineering programs for 22 years, has a chapter regarding non-inertial coordinate systems, and their conversion to an inertial approximation using fictitious forces–all of these forces have names–translational, azimuthal, centrifugal, coriolis. I don’t see that explanations invoking these fictitious forces are just plain wrong, and that is the one and only criticism I had of Willis’ essay.
If nothing else this essay has certainly set off a busy thread.
Kevin Kilty says:
February 18, 2014 at 2:00 pm
We may be talking past one another here, but I don’t see that anyone on this thread denies that gravity is the “cause” (forcing) of the tides, but you, yourself, used the term “tidal effect” which suggests to me what we ultimately observe as the tides–i.e. things beyond the cause.
By ‘tidal effect’ I meant the effect derived from the static difference between gravity on the two sides of the planet. Using fictive forces for ‘ease’ of calculation is OK as long as you get the same result. The standard treatment in tide theory has no need of fictive forces, see e.g. page 537 [equation (2.4) ff) of http://www.leif.org/EOS/Munk-Tides-1966.pdf for the derivarion of the potential. It is sad that this thread has turned into a pissing contest.
lsvalgaard says:
February 18, 2014 at 2:15 pm
Actually I don’t think it is sad even if if occasionally it looks like a pissing contest, because there are things to be learned from reading the thread. For instance your reference to the paper by Munk, which I was not familiar with, is my take-away here. It has become a sort of peeve of mine that people have no trouble with dynamical terms appearing on the right-hand side of F=ma as inertial terms, but then suggest that it just wrong to put them on the left-hand side and give them funny names. There are many ways to work problems, and, as you say, what matters is that one get the correct answer.
Mike M. says:
February 18, 2014 at 1:13 pm
“Yeah… okay. It’s a circular orbit for the purpose of illustration so they can be on opposite sides of the sun for all I care.”
It that case they will exhibit the same behaviour as regards speed/radial velocity, etc. Stable orbit anyway.
RichardLH says:February 18, 2014 at 3:36 pm “It that case they will exhibit the same behaviour as regards speed/radial velocity, etc. Stable orbit anyway.”
Nope, one of them is going slower by 463 M/sec so it has to have another force acting on it, (pointing away from the sun), to keep it in a stable orbit because the sun’s gravity is providing too much centripetal acceleration for that orbital radius at that slower speed.
It’s all about the gravity, strictly in the interests of science.
SI swimsuit edition cover girl Kate Upton in Zero G (string):
http://www.today.com/entertainment/kate-upton-flips-spins-bikini-zero-gravity-sports-illustrated-2D12124620
Mike M says:
February 18, 2014 at 4:00 pm
“Nope, one of them is going slower by 463 M/sec so it has to have another force acting on it, (pointing away from the sun), to keep it in a stable orbit because the sun’s gravity is providing too much centripetal acceleration for that orbital radius at that slower speed.”
I obviously do not understand what it is you are trying to plot. Where does the 463 M/sec come from?
Can you provide a diagram marked up with what it is you are tying to show? Just a simple vector plot should do.
Mike M says:
February 18, 2014 at 4:00 pm
Try this for starters.
http://i29.photobucket.com/albums/c274/richardlinsleyhood/EarthSun_zps14b35168.png
So where are your two particles?
denniswingo – I forgot to ask, at what latitude are the accelerometer measuring that?
It was at 34.85 degrees N 86.99 W (Huntsville Alabama)
I have my experimental hardware back and will be hooking it up in a few weeks. I have been able to “watch” the Moon go overhead by watching the output of our accelerometers change (sensitive to ~+/-1 micro gee).
I used to have all of the numbers in my head on these things but I could be off. Will play with my hardware soon.
Personally I don’t think of these things as “tides” in the way that Willis does. We look at the equipotential surfaces and that the water bulges because it is slightly farther “uphill” in the gravity well. That is just us physicists talking though…..
denniswingo says:
February 18, 2014 at 5:53 pm
Personally I don’t think of these things as “tides” in the way that Willis does. We look at the equipotential surfaces and that the water bulges because it is slightly farther “uphill” in the gravity well. That is just us physicists talking though…..
—
Now that’s a great way to look at it and is more the way I view it also, not only speaking of just the bulge but the tangential acceleration component that starts the water to flow which then builds momentum and inertia that when obstructions, like shores or opposite flows, are encountered can cause the actual time of high tide locally to either precede or lag behind the moon’s exact passage directly overhead even also adjusted for the sun’s influence, due to that momentum that may have already reversed to outflow, depending on the actual topography that disperses that built up momentum, or that the view I have held for a long, long time. It all depends on the slosh and how steep and deep horizontally the obstructions are that counter the flow. Sorry for the running sentence.
lsvalgaard says:
February 18, 2014 at 9:59 am
“Under the assumption that the rotation rate is that of a tidally locked moon [not a bad assumption], the rotational role of the breakup is to raise the factor from 2 to 3.”
I will take that as concession that the differential acceleration factor is, indeed, 6 and not 4, as I have been trying to explain to you.
” If it does not rotate at all, then only the tidal effect plays a role.”
As we are dealing with “fictitious” forces, the frames of reference play a key role, and we must define them carefully. In the particular case of a tidal locked orbit, the force can be looked upon as due to centripetal acceleration in one frame, and pure spin in another. They are entirely equivalent in terms of their ultimate effect.
What you call not rotating at all, I can as easily call the effect of angular momentum being cancelled by spin in the rotating frame.
“This has nothing to do with the orbital centripetal acceleration in causing tides, and is thus irrelevant.”
There you make the elementary mistake of assuming that first order necessary conditions for an equilibrium are also sufficient. Although uniform expansion is an equilibrium solution of the dynamic equations, it is an unstable one. Failure to take into account second order sufficient conditions for stability has played a role in many engineering disasters. A prominent one, often used as a cautionary tale for aspiring engineers, is the failure of the Explorer 1 satellite, the first artificial satellite launched by the United States.
In space, bodies always seek their minimum energy configuration. And, that minimum energy configuration is with the steady state minor axis of inertia pointing towards the gravitating body, and spinning about the major axis, i.e., a fluid body will always end up bulging along the +/- radial direction in steady state. And, part of that bulge will be due to the centripetal acceleration which, as you have conceded, produces 3/2 larger differential stress due to the centripetal acceleration.
denniswingo says:
February 18, 2014 at 5:53 pm
“Personally I don’t think of these things as “tides” in the way that Willis does. We look at the equipotential surfaces and that the water bulges because it is slightly farther “uphill” in the gravity well. That is just us physicists talking though…..”
They are just trying to break that varying equipotential surface into its sine wave components – now where have I heard of that approach before 🙂
Bart says:
February 19, 2014 at 1:46 am
I will take that as concession that the differential acceleration factor is, indeed, 6 and not 4, as I have been trying to explain to you.
No, this is irrelevant as I have been trying to explain to you. If a body is rotating fast enough, the rotation in itself will cause a bulge which has nothing to do with tides.
As we are dealing with “fictitious” forces, the frames of reference play a key role, and we must define them carefully. In the particular case of a tidal locked orbit
It is not the orbit that is tidally locked, but the rotation of the body that is locked. Here you show your confusion.
And, part of that bulge will be due to the centripetal acceleration which, as you have conceded, produces 3/2 larger differential stress due to the centripetal acceleration.
You are still confused.
lsvalgaard says:
February 19, 2014 at 3:59 am
Bart
“And, part of that bulge will be due to the centripetal acceleration which, as you have conceded, produces 3/2 larger differential stress due to the centripetal acceleration.”
Leif
“You are still confused.”
So confused so as not to realise that most of the centripetal acceleration shows up in the rock, not the water anyway.
RichardLH says:
February 19, 2014 at 4:18 am
“And, part of that bulge will be due to the centripetal acceleration which, as you have conceded, produces 3/2 larger differential stress due to the centripetal acceleration.”
The Roche Limit is how close a body can get to another [larger one] without breaking up. If the body rotates fast enough it will break up regardless of any tidal effects. In the general case, the breakup is determined by both fast rotation and tidal forces working together, having nothing to do with any orbital accelerations. I can only encourage bart to study the Munk reference I gave him to learn about how to calculate the shape of the ‘gravity well’ Dennis referred to.
lsvalgaard says:
February 19, 2014 at 4:31 am
“The Roche Limit is how close a body can get to another [larger one] without breaking up”
I do know what the Roche limit is.
I was just pointing out that most people seem to be asserting that centripetal acceleration affects the oceans, whereas it mostly affects the rock on which the oceans are but a very thin skin.
RichardLH says:
February 19, 2014 at 4:36 am
I was just pointing out that most people seem to be asserting that centripetal acceleration affects the oceans, whereas it mostly affects the rock on which the oceans are but a very thin skin.
Of course you know, but bart does not, so a bit of explanation for his benefit. In addition, the bodies for which the Roche Limit is important have no oceans, being just piles of rock [which may be made of ice]. Comets are such bodies and are not ‘tidally locked’.
lsvalgaard says:
February 19, 2014 at 4:47 am
“In addition, the bodies for which the Roche Limit is important have no oceans,”
The chance of a body still having an ocean by the time it reaches the Roche limit is likely to very small 🙂
I suppose if one were to posit a very elliptical orbit you might be able to get one with the other though I suspect it would have boiled away long before closest approach!
I grabbed my old college textbook on classical mechanics on the way out the door (Barger and Olsson) and had a few moments to read the section on the tides before my Thermo class this morning. They derive the tidal potential by 1)switching to an inertial reference frame, 2)write a potential gotten from the centrifugal force and using the binomial theorem to write an approximation for distance from the moon to an ocean particle on Earth. This is exactly the approach I suggested doing days ago, which got me a rebuke from both you and Willis. This was 42 years back in my memory, but old habits die hard. I rest my case about the dynamics of the system being pertinent to the problem. I now intend to read Munk, who I expect follows Lamb in this regard, and I bet dimes to donuts that there is an implied use of the dynamic “ma” term in there someplace.
Kevin Kilty says:
February 19, 2014 at 12:09 pm
The problem with using centrifugal force and the oceans is that almost all of the centrifugal force goes into the rock not the water.
6,378.14 kilometres of rock (average).
3.8 kilometres of water (average)
is a very hard ratio to contest!
This has been a most interesting thread. It was very difficult to toss out centrifugal and centripetal forces from my mind. Now I can’t constrain my thoughts when thinking outside the earth, Every time I close my eyes my brain jumps in gear analyzing a planet/moon system traveling to or away from a distant gravitational force. If not that then analyzing the same planet/moon system orbiting that same distant gravitational force. And then there’s the issue with elliptical orbits. And of course changing the size relationship between the planet/moon. Yeah, of course that brings up the angle of the center line through the ellipse off from the general direction of travel of the various planet/moon systems my brain wants to play with.
It sort of looks like a big drunk and a little one trying to walk around an incline while keeping a bungee cord tight. LOL
Willis, thanks for the insight to that which I was blind.
Just wonder how the tidal forces on a space-lift would be. You know the thing described by Arthur C. Clarke; a lift which goes from equator all the way up to the geosynchronous orbit and beyond.
Let’s for simplicity say that the chosen length is twice the distance to the geosynchronous orbit. This structure can in theory be built as free floating satellites just hovering 1 meter over the Earth’s surface and stretching 2x geosynchronous orbit into space.
The tidal effect caused by the gravity would be close to one G. It is 1 G in the lowest point, and nearly nil in the upper point.
But an astronomer in the lift would experience twice that tidal effect. In the upper point it would be one G outwards, giving a total tidal effect of 2G.
Doesn’t this imply that one also have to take the centripetal force into account?
/ Jan
Kevin Kilty says:
February 19, 2014 at 12:09 pm
l
Kevin, I re-posted this link above, and I re-post it here, for a simple reason.
It distinguishes clearly between fictive forces and real forces, and it does so using five different frames of reference. One of them is the “inertial reference frame” you speak of above.
The key insight in the question is encapsulated in his conclusion, viz (emphasis mine):
Note that his statement, that rotating around the CM doesn’t produce any tidal deformation, is not an unsupported claim. It is supported and explained by the detailed mathematical calculations that he provides for each of the five different reference frames. In every case, the result is the same … “centrifugal force” doesn’t produce tidal deformation. It just makes the calculations more complex.
w.
Willis, you, Leif, and I will have to agree to disagree on this; or maybe we are arguing against different things here. The derivation in Barger and Olsson settled the issue in my mind this morning. It was abundantly clear. By the way, I never argued that you had done this wrong–rarely do I find much to argue about in your efforts. I like your essays. I was arguing initially against what I perceived as a blanket statement that use of a repulsive force (“centrifugal”) is just plain wrong. I may have misunderstood that.
Best wishes always.
How can something so simple be so hard to explain?
I tried several times to make the simple explanation to help those here and every time it don’t come out right or at least not the way I intend.
WOW, Willis said it was a short post!
I’ve got some text docs (mime) and hope to put /combine/edit/compile/etc with regards to this discussion.
I had a difficult time with this and when it finally clicks you may say WTF was I thinking.
Think “corkscrews”.
lsvalgaard says:
February 19, 2014 at 3:59 am
“No, this is irrelevant as I have been trying to explain to you.”
And, you are wrong. There is a factor of 3/2 amplification of the differential. You’ve admitted it.
“It is not the orbit that is tidally locked, but the rotation of the body that is locked. Here you show your confusion.”
It is not I who is confused. You are defining your fictitious forces with respect to an accelerated coordinate system, a big no-no in Newtonian mechanics.
“You are still confused.”
I have no more time to waste on you, Leif. Once again, you put on a big show, but it’s all hat and no cattle.
RichardLH says:
February 19, 2014 at 12:20 pm
You guys are clueless.
Jan Kjetil Andersen says:
February 19, 2014 at 12:51 pm
“Doesn’t this imply that one also have to take the centripetal force into account?”
Yes. In fact, the calculation of tension in such a structure depends very explicitly on the centripetal acceleration term. It magnifies the tension by a factor of… wait for it… 3/2.
Willis Eschenbach says:
February 19, 2014 at 1:04 pm
“This condition is equivalent, in every case, to the free fall condition.”
I explained previously why your source is trivially wrong. The entire Earth is not in free fall. Only the center of the Earth is in free fall. Everything else is being pulled along for the ride. This is what gives rise to tidal stresses in the first place.
This is pointless. I’m done with this thread.
Bart says:
February 19, 2014 at 9:26 pm
This is pointless. I’m done with this thread.
You could learn something from http://www.leif.org/EOS/tides_CHT_thesis.pdf
Bart says:
February 19, 2014 at 9:26 pm
You are defining your fictitious forces with respect to an accelerated coordinate system, a big no-no in Newtonian mechanics.
Not at all, it is much simpler than that, see e.g. section 5.2 of http://www.leif.org/EOS/tides_CHT_thesis.pdf
Study the thesis carefully and you’ll see.
lsvalgaard says:
February 19, 2014 at 10:13 pm
Bart says:
February 19, 2014 at 9:26 pm
You are defining your fictitious forces with respect to an accelerated coordinate system, a big no-no in Newtonian mechanics.
Not at all, it is much simpler than that, see e.g. section 5.2 of http://www.leif.org/EOS/tides_CHT_thesis.pdf
Study the thesis carefully and you’ll see.
lsvalgaard says:
February 19, 2014 at 10:16 pm
Poorly done.
Bart says:
February 19, 2014 at 9:26 pm
“You guys are clueless.”
What? To point out that all (well very, very nearly all) of any centripetal acceleration is exposed in the rock? That is the reality of the situation. If there were no ocean at all (and no Moon to boot) the globe would still be an oblate spheroid with approximately the same dimensions. Add in the oceans. Then there would be a small, easy to calculate Solar tide and that would be that. One application of the Solar gravitational field ala Wiki field vector plan. Easy stuff. Small variations due Earth orbital changes.
Now adding in the Moon is what adds the complications. But that is just a more complex form of what we have shown already. With complex, interleaved patterns that beat away with the Solar stuff.
And then we stand a chance of not getting things in the wrong proportions or from the wrong causes.
Bart says:
February 19, 2014 at 9:26 pm
Bart, the issue was not the conclusions. I provided a link, not for the conclusion which I quoted here, but for the elegant exposition of the mathematics of tidal forces. The math is derived using five different frames of reference. The paper is beautiful, with moving graphics illustrating each frame of reference. Heck, he even derives the result using the reference frame of an observer on the moon. I explained that in all five of them, the centrifugal/centripetal forces cancel out mathematically.
Your claim that your “explanation” and your unsupported statement that “the entire Earth is not in free fall” trumps five pages of math is hilarious. This is SCIENCE, Bart, not grade school. You can’t beat math with your mouth.
To beat math, you have to show where the man’s most clear and elegant math is wrong. Not claim that it’s wrong. You have to show where it’s wrong. All you’ve done so far is talk. Talk doesn’t trump math.
So I can see why you want to say “I’m done with this thread” and go out the door. It’s because you can’t show where the math is wrong. Not because of your math-fu, however. That may be very strong, but it wouldn’t help. You can’t show where the math is wrong, simply because the math is correct, and has been well understood for a long time.
Now, that leaves you with a choice. What I would do in your position is first verify that I couldn’t find any mistakes in the math. Then I’d slap my forehead and say “Dang! I checked the math, I understand every step of it, and guess what? Looks like I was wrong after all!”.
That way everyone congratulates you, because that’s what scientists do—admit when they are wrong. That way, your credibility here at WUWT goes up.
Or you can just say “I’m done with this thread” and walk away. At that point, you might as well not post at WUWT again, because you’d be left without a scrap of credibility. Everyone here knows nobody can beat math with their mouth. And everyone here knows that you personally can’t demonstrate any errors in the math I linked to, because it’s basic stuff that’s been known for centuries.
So, the choice is yours. To encourage you to take the scientific direction, let me point to a past post of mine entitled Wrong Again … and I was, too. It’s one reason that even people who dislike me still read my scientific ideas and research—because they know that when I’m wrong, I stand up and say so loud and clear.
w.
I think a spacelift is a useful analogy for analyzing this topic.
Imagine a rod twice the length of the distance to the geosynchronous orbit. The rod is placed vertically in the geosynchronous orbit and stretching all the way from the Earth surface to twice the height of the geosynchronous orbit. A counterweight is placed in the upper end to stabilize the rod in an orbit where the lower end is hovering one meter above a point at the Earth’s surface at the equator.
This will be a satellite to the Earth and will be subject to the same tidal forces as any satellites. However, the extreme dimensions of this structure highlight the tidal effects.
The lower end will have gravitation equal to one G. The gravitation at the upper end will be about 1% of that. A 100 kg body will weigh 100 kg at the lower end, and the same body will have a gravitational pull of 1 kg force in the upper end. But the centripetal force in the upper end will drag the body outwards with approximately 4 kg force, giving a net outward force of 3 kg.
That means that the tidal force, calculated in the way Willis does above, give a force of 99 kg on the 100 kg body, but when taking centripetal acceleration into account we get a force of 103 kg.
As I see it, this must mean that we have to take centripetal acceleration into account when we calculate tidal force.
Or can anyone find an error in this reasoning?
For spacelifts see:
http://www.spacelift.org/
/Jan
Jan Kjetil Andersen says:
February 20, 2014 at 12:23 pm
But the centripetal force in the upper end will drag the body outwards with approximately 4 kg force, giving a net outward force of 3 kg.
some confusion: the centripetal force is directed towards the Sun being just the gravitational force]. The centrifugal force is directed outwards, but is the same for all points of the Earth.
lsvalgaard says:
February 20, 2014 at 12:33 pm
Thank you Leif, I should have used the word “centrifugal”, not “centripetal”
I would appreciate if you also would comment on my reasoning of the combined tidal effect of 1.03 G on the spacelift.
Do you agree that an astronomer on the spacelift would experience a tidal variation of 1.03 G between top and bottom?
If so, how can this be explained by gravity alone?
/Jan
Jan Kjetil Andersen says:
February 20, 2014 at 12:42 pm
Thank you Leif, I should have used the word “centrifugal”, not “centripetal”
I would appreciate if you also would comment on my reasoning of the combined tidal effect of 1.03 G on the spacelift.
It is a bit more complicated than that as gravity itself decreases with altitude. The lift would not be standing on the ground, but hang from the anchor point at geostationary orbit where the total force on it would be zero, and built simultaneously up and down to balance the weight of the cable.
Now as to the tides: The rotation of the Earth already raises an equatorial bulge of 21 km [or a 100,000 times greater than the solar tide]. This is not a tide and the tension in the cable is also not due to a tide.
lsvalgaard says:
February 20, 2014 at 12:56 pm
Now as to the tides: The rotation of the Earth already raises an equatorial bulge of 21 km [or a 100,000 times greater than the solar tide]. This is not a tide and the tension in the cable is also not due to a tide.
On the other hand the space lift is influenced by both the lunar and solar tides as everything else is. Here is an analysis of what the normal tides will do to the lift:
http://repositories.tdl.org/ttu-ir/bitstream/handle/2346/21793/Kaithi_Vijaya_Thesis.pdf?sequence=1
lsvalgaard says:
February 20, 2014 at 12:56 pm
I agree on all that, but it does not answer my question so let me rephrase.
I am talking about the spacelift as a satellite to the Earth, and I am discussing the tidal forcing experienced on that satellite from the Earth.
For simplicity, let us forget about the Sun and the Moon because that is not the tides I want to analyze with this example.
The spacelift is a rod or a cable and let us say the anchor point is in 2x geosynchronous height, that is 71 600 km above the Earth surface. In that anchor point the Earth’s gravity will be approximately 0.01 G.
That means that an astronaut with a weight of 100 kg will have a gravitational pull of 1 Kg towards the Earth in that point.
But the centrifugal force caused by the Earth’s rotation will push the astronaut outwards with a force of 4 kg. The net force experienced by the astronaut will therefore be 3 kg outward, or -0.03 G.
In the lower point the gravity will of cause be 1 G.
That means that the total tidal force on board the spacelift satellite is 1.03 G.
/Jan
Leif:
“Now as to the tides: The rotation of the Earth already raises an equatorial bulge of 21 km [or a 100,000 times greater than the solar tide].”
You would think that at that point people would stop and go ‘duh – the rock centripetal is 20 km, the water tidal is less a than a meter plus/minus variation on that’ but no……
Jan Kjetil Andersen says:
February 20, 2014 at 1:27 pm
“I am talking about the spacelift”
The problems with the ‘spacelift’ concept is one that is rarely discussed. In order for the far end anchor point to stay immediately above a point on the equator requires the lift rod to push it faster than orbital sped at that height. It cannot be a cable as otherwise it will drift back against the spin in some form a curve. That extra, outwards, centripetal force has to come from somewhere you know, it doesn’t just create itself. It must come from tensions/torsions in the ‘rod’ that maintains its position vertically above the surface anchor point. The rod also has to supply the tangential acceleration required to any object travelling up it to get it to the required ‘top end’, tangential velocity.
RichardLH says:
February 18, 2014 at 4:45 pm
http://i29.photobucket.com/albums/c274/richardlinsleyhood/EarthSun_zps14b35168.png
So where are your two particles?
————————-
I appreciate you drawing that. Thanks and I intend to produce a free body diagram for particles at, per your sketch, that are at positions “A” or “B” versus either “C” or “D”.
Doing this via FBD is more involved but there are only two general factors – sum up the forces acting on the particle that produce the radius of curvature of it’s path at that point in time and at it’s velocity WRT to the center of the sun at that point in time. We already have the velocity per all the above discussion so providing a summation of forces and a value for radius of path curvature comprise the task ahead. It will reveal why we weight less at noon and midnight than at 6am/pm by an acceleration factor of .00018 meters/sec^2 at the equator.
I haven’t had time to do it yet – I promise I will this weekend.
I’m just a country bumpkin and continue to drop in on this discussion from time to time ’cause I needed more shotgun shells to shoot the squirrels and rabbits I need for dinner and have an inquiring mind.
I want to bring up a thought experiment that is only a very simple and elementary view that may help to explain what Willis and Lief are showing. Maybe it’s enough to get the very intelligent minds here focused in the same direction.
You must understand the concept of Willis’ three weight (with blue rope) diagram and an external gravitational force applied with the direction of attraction being applied running in the same direction as the blue rope.
I may wish I never post this, but here it goes. You will not need any concepts of centrifugal/centripetal force. Freeze frame the entire universe (i.e. nothing is in motion/moving). Consider that there is only one very distant body in that universe and it (due to it’s mass) has a gravitational force. The other bodies are your experimental weights/bodies.
You don’t even need to know what direction that distant gravitational force is coming from because with only two of those weights/bodies (Willis’) using a red rope between them you can find out. Consider that you have no mass so as to not affect this thought experiment.
Please note that in the first case I am only considering the effect of releasing the weights/bodies inline with a distant gravitation pull. In the second case I’m releasing them with the rope perpendicular to that distant force. For simplicity in this thought experiment let’s skip what would happen with the weights being released in an orientation other than the red rope being aligned in an orientation that is not perpendicular or inline (parallel with) the distant gravitational force. That makes things a little more difficult and would detract from this most basic example (but by all means do it later as that’s where things get interesting).
Now release the two equal size/mass weights/bobies (with the red rope taught) and watch them. If the the rope begins to slacken then you have placed the weights perpendicular to the direction of the distant source of gravity. They are now accelerating in the direction of the distant force equally and at the same time attracting each other equally. They will come together. As with Willlis’ simple diagrams there will be a bulge with no centrifugal force necessary. Some inertia as a result of the difference in acceleration due to the diameter of the two weights/bodies as the two weights/bodies (with red rope) accelerate towards one another but remember they are NOT spinning/orbiting. Now think this all through again using bigger weights/bodies. The bulge will become more obvious.
Willis has already explained the case where the weights/bodies are in alignment with the forces of gravity and used a blue rope. You have already thought about that so I’ll skip it.
Now for the fun part. Consider releasing the two weights/bodies with the red rope at a 45 degree angle in orientation to direction of the distant gravitational force. Then for fun do all this again and use two different size/mass bodies. Close your eyes and let your brain play. Then un-freeze the universe and watch what happens.
There a lot of warts associated with this vague description . Cut me some slack until you read the next comment from me.
This not so organized bunch of words that I have placed on digital paper may not be absolutely clear but hopefully will help some get a start to the concept of what Willis has correctly explained. Now back to the woods with another box of 20 ga. shot shells.
I’m stunned that this thread is still running, albeit slowly, so many days after its birth, but I am glad that you brought this thought-experiment up, because you are one commenter here who now believes that you do not need centripetal/centrifugal forces to make proper explanations of things.
Let me make the following points.
1) If centrifugal force wasn’t a useful concept, then Coriolis force wouldn’t be either, because they both originate in the same way. Moreover, why do mechanics textbooks used in upper division physics courses, and also engineering mechanics courses, have sections of the text devoted to this topic of fictitious forces, complete with example problems, if the concepts weren’t needed or useful?
2) I have consulted the Barger and Olsson (B&O) textbook, which is a very good upper division text from which to learn classical mechanics by the way, and found that to explain the tides on Earth as raised by the Sun they actually state the impact of the “centrifugal force” of Earth’s orbital motion around the Sun. Then they derive the tide-raising potential by adding a potential function based on this centrifugal force to the gravitational potential.
3) I decided to consult Horace Lamb’s book “Hydrodynamics” (1932) on the subject. Leif has been pointing everyone, including me, to a paper by Munk as proof that one needs no more than gravity to make the tide-raising potential, but Munk in turn references Lamb, so let’s go straight to the horse’s mouth on this subject. Lamb derives the tide-raising force in a different manner than B&O, but it is explicitly clear that he uses also uses the centrifugal force to make a contribution to the gravitational potential.
4) Why do these eminent authors use the centrifugal force? Because it is absolutely essential to getting the potential function correct, that’s why. The reason is this: If you write the gravitational potential of the Moon in a Taylor series referenced to the center of the Earth, you will obtain a term proportional to “radius of the Earth times cosine of latitude” that is not part of the tide-raising potential. The centrifugal force just happens, not coincidentally, to provide what’s needed to cancel this.There is no way to eliminate this term otherwise and obtain the correct form of the tide-raising force.
5) Willis uses free fall rather than centripetal acceleration to provide the offsetting term, which I have no objection to, but keep in mind that free-fall and centripetal accelerations are not the same thing. Free-fall acceleration is an increasing speed of an object tangential to its path; centripetal acceleration results from changing direction and is perpendicular to the path. In both instances they provide something needed to get the tide-raising force right; but I feared that people would learn from all of this that centrifugal forces are fictional and never needed because they complicate the picture, and there is something fishy about centripetal acceleration as well. You appear to have done just that.
6) Leif, Willis, and some others here believe the forcing function for the tides is just gravity and this is a problem in mechanical static equilibrium–or at least that’s how I interpret their reaction to all I say. But the essential function of either free-fall acceleration or centripetal acceleration in deriving the tide-raising potential shows that even equilibrium tides are a dynamic phenomenon.
I hope this clears up some of your confusion.
Kevin Kilty says:
February 22, 2014 at 10:49 am
4) Why do these eminent authors use the centrifugal force? Because it is absolutely essential to getting the potential function correct, that’s why.
Since the centrifugal force is the same for every point on or in the Earth, it cancels out when you compare the forces on any two points, e.g. the subsolar and the anti-solar points, and hence does enter into the expression for the difference between the forces and thus also not for the height of the tidal bulge.
Here we are all talking about the special case of an object(earth,moon) in orbit around another object (sun-earth-moon barycentre). In this special case the centrifugal force is perfectly balanced by the centripetal force(gravity). This is the same case for the space station in orbit around the earth where astronauts are essentially weightless. As a result of the earths orbit(s) we being attached to the earth don’t feel the gravitational force of either the sun or the moon. We only feel the gravitational attraction of the earth.
Now consider an asteroid passing close by the earth. It gets deflected by the earths gravity and feels a centrifugal force which is not equal to the centripetal force(gravity). Now work out the tidal force exerted on the object of radius R. Now you must include the centrifugal force !
Kevin Kilty says:
February 22, 2014 at 10:49 am
“Lamb derives the tide-raising force in a different manner than B&O, but it is explicitly clear that he uses also uses the centrifugal force to make a contribution to the gravitational potential.”
Oh there is a component to the water tides that is centripetal. But it is very, very tiny.
The majority of the centripetal force is expressed in the rock. All 21 km or so of it. Then we get approximately 1 m or so of Earth tide. Then we get a few mm or so of water centripetal. Then we get a few 10’s cm of water tide (open ocean – no land).
Do the maths. You’ll se I’m right.
Remember, if there were no oceans, the Earth would still be an oblate spheroid with a 21 km bulge.
Richard LH,
Thanks for your reply. You are speaking of the centrifugal force pertaining to the Earth’s rotation on its axis; I am speaking of the centripetal acceleration pertaining to the orbital path around the tide-raising body. They are utterly different things.
Kevin Kilty says:
February 22, 2014 at 11:26 am
I am speaking of the centripetal acceleration pertaining to the orbital path around the tide-raising body.
Since the centripetal acceleration [directed towards the sun] is just gravity [what else holds the Earth in orbit?], you must mean the centrifugal force.
Lsvalgaard,
Good grief, you got in here even before RichardLH. You and I are saying almost exactly the same thing in two different ways, I think, but I was really refering to the potential, not to its gradient, and I think one ought to say really that the centripetal force equals the gravitational attraction of the tide raising body at its centroid. By the way Lord Kelvin spoke not just of lunar and antilunar points, but of a moon and antimoon, at least according to Lamb. I have no idea if such a concept helps someone understand the tides or not–I’d say not.
Kevin Kilty says:
February 22, 2014 at 11:39 am
and I think one ought to say really that the centripetal force equals the gravitational attraction of the tide raising body at its centroid.
The centrifugal force due to orbital revolution is the same at all points of the Earth and is equal [but in opposite direction] to the centripetal acceleration = the gravitational acceleration at the center of the Earth.
Kevin Kilty says:
February 22, 2014 at 11:26 am
“Thanks for your reply. You are speaking of the centrifugal force pertaining to the Earth’s rotation on its axis; I am speaking of the centripetal acceleration pertaining to the orbital path around the tide-raising body. They are utterly different things.”
You want to do the maths?
Earth rotation 0.034 m/s^2
Earth orbital ~0.0000952 m/s^2
Kevin Kilty,
There is only acceleration and deceleration involved. Get back in space in my thought experiment. There are only three forces involved. (1) Gravitational attraction between the two experimental bodies, (2) gravitational attractions with the distant body/force, and (3) inertia (decreasing and increasing) as a result of the gravitational forces involved. I used in my thought experiment a case where two weights/bodies were being effected by a distant gravitational force/attraction.The speed of the bodies would increase toward that distant force but would be in a sense a “stop and go” approach and kind of in a zig zag manner from an individual viewpoint.
My thought experiment didn’t include a thought experiment of the two weights/bodies already in orbit. The reason for that is that it’s not likely anyone would have stayed with this thread were they not pretty intelligent.. If one who has been following this thread this long and grasp something from my contribution you can “bet your ass” they immediately applied that to a planet/moon system in orbit around a much larger body/sun.The results would be similar, just that the distant force would now be a 90 degree angle from the general planet/moon direction at any given point in time. In this case the distant force is maintaining a relatively steady orbit (practically speaking but likely an ellipse of sorts) and not increasing the speed/velocity of this planet/moon system toward that distant force/body.
Forget the centrifugal and centripetal force. The only forces are only gravitational attraction and inertia. Look an earlier post where I commented that it would look like a big drink and a smaller one running around trying to keep a bungee cord taught while they walk down the road. As they go down the road they will need both lanes.
Willis and Lief are correct in the concept.
If you can grasp what I’m trying to show then the tides (as we want to relate to water) is a piece of cake
Lief and/or Willis, don’t go away. I need some clarification on the Roache limits. I’ll see if i can comment ASAP.
It’s one of those things I just gotta know.
Here are a couple of thoughts I have orbiting in the gray regions of my gray matter. I gotta ask rather than state, but my brain don’t wanna let go. Consider the case where a planet/moon system were to be on a trajectory towards the earth’s sun. It is not in orbit around the sun but headed directly (as much as can be stated in a warped time/space concept) towards the sun due to that gravitational attraction between the two (sun and planet/moon system). Now my brain is entertaining thoughts that as this planet/moon system approaches the sun that the orbital relationship will change to a more elliptical configuration and at some “sweet spot” near the point where the sun’s gravitational pull equals the planet’s gravitational pull will cause the planet and moon to collide. If this could be possible then would that occur before the Roache limit is reached? Oops, the Roache limit would be dependent on the axial/rotational velocity of the planet or moon and also on the composition of those so consider something like maybe Mars or Earth’s moon. In my desire to limit words on this I hope I have given you the idea/concept that is on my mind. So I guess the general question is: Would the planet and moon likely collide before the Roache limit of either is reached or would we we looking at a “sweet spot” where they could be close to the same point?
Then of course that would bring up the direction of an angle of approach of an hypothetical planet/moon system from the cosmic depths (with consideration of a relationship to the orbital plane that the sun’s (earth included) planets lie). These thoughts seem to be directed towards that orbiting (around the sun) belt of rocks between Mars and Jupiter. Does anyone really know where the rocks (in orbit around the sun) came from?
Time constraints (on my part) limits my expression of thoughts/explanation much. Please cut me some slack for an incomplete explanation, after all those still here are having issues with an explanation/consensus. But if you can interpret my thoughts I would really appreciate some discussion. Let me say this, I agree with Willis and Leif in what has been presented.
I just went somewhat off topic in my thoughts but those thoughts are directly related to the concept of this thread. Ohh, the unconstrained mind.
Gotta go, I saw a rabbit run into a brush pile over yonder.
eyesonU;
Ro[
a]che LimitYore spellin’ bugs me.
There’s a reason Willis’ scenario involved a stationary sun and moonless planet, falling directly (not orbiting). 3-body orbital mechanics are currently insoluble, beyond brief (cosmically speaking) periods.
For more phantastical speculations, come up with explanations for Venus’ retrograde and very slow (but not quite tidally locked, unlike Mercury’s) rotation (but conventional orbit). Probably involves flipping at some point. Maybe discarding a moon, which became Mercury?? Rabbits galore!
There’s also a Rock limit, which is the closest distance a even a mineral or metallic meteorite/comet can get to the sun without vapourizing.
Brian H says:
February 22, 2014 at 5:41 pm
==========
I have to agree with you about the spelling. Got a lot of thoughts in my head that weren’t there when this thread began. Trying to pull ’em out and write ’em down before this thread dies put me under pressure.
My brain has been having a great time with my new found knowledge as a result of Willis’ post. And it ain’t over yet!
Brian H says:
February 22, 2014 at 5:41 pm
==============
Now you got me thinking about Mercury/Venus idea to go along with my hypothetical possibility of a planet/moon collision as mentioned earlier. Venus does rotate about it’s axis opposite the other planets. A side swipe collision at an orbital location between Mars and Jupiter would have left a debris field and probably separated the two with momentum towards the sun and separate orbits. Now just have to figure out an angle of approach towards the sun and we got us a brand new theory. LOL
If anyone is still following this thread please stay tuned. My brain is acting like a good bird dog and may have sniffed out the track of a couple of celestial rabbits and seems to be on point now. Kept waking me up all night.
I’m going to try to pull my thoughts from the deep regions of my mind and put ’em on digital paper today.
I might be nuts so it could be interesting to watch me go off the deep end right here on WUWT. But then maybe not. Hard to say as I’m talking to a computer screen at the moment! ROFLMAO
Leif, where are you?
eyesonu says:
February 23, 2014 at 9:37 am
Leif, where are you?
Still here, but ‘im Westen nichts neues’.
clivebest says:
February 23, 2014 at 3:01 am
Thanks for that, Clive, but I’m sorry—you still don’t need centrifugal force. Here’s a thought experiment to show why.
Suppose you are in an elevator in free-fall in space. Now, suppose you end up “passing close by the earth”. Do you experience any centrifugal force? For example, as the elevator’s path is curved by passing the earth, are you slammed up against the elevator door like you get slammed up against the car door in a car going around a tight corner?
Nope. Not in the slightest. There is no discernible force exerted on you that would sling you to the outside. You could slingshot around the earth and get slung in the direction of Jupiter … and from inside the elevator, you’d never know it. As far as you are concerned you are in undisturbed free fall. Getting slingshot past the earth has absolutely no impact on you … EXCEPT for the tidal effect. That tidal effect you can measure from inside the elevator.
But it is totally separate from the centrifugal force, which you cannot feel at all inside the elevator. This means that from the perspective of the elevator, we do NOT need to include the (undetectable from within the elevator) centrifugal force exerted by passing close to the earth.
Regards,
w.
Willis,
Sorry to drag this on yet again ! However lets consider that the asteroid consists of your 3 masses joined together with springs. As they approach the earth an observer on the first mass begins to see that the spring tension gradually increase as the other two masses apparently start to repel each other and move apart. At closest approach the separation reaches a maximum and so does the tension in the spring. However gradually the tension begins to reduces until eventually the separation of masses are exactly the same as they were before.
Then the observer looks outside and finds that the star constellations have dramatically changed. Everything has now been rotated by 70 degrees. He therefore concludes that a torque has been applied to his system.
The real mystery here is the equivalence of inertial mass and gravitational mass. General relativity kind of explains this by explaining that mass/energy distorts space-time. Your lift shaft or free falling object then becomes a geodesic in curved space.
Would a spin dryer still dry clothes in an empty universe ? Centrifugal forces are not completely trivial.
This is the only point I want to make.
Willis Eschenbach says:
February 23, 2014 at 10:38 am
“Nope. Not in the slightest.”
Wrong. This would only be the case if your CG were precisely coincident with the CG of the elevator. If it is off even a smidgeon, you would be pushed to the wall in the direction of your CG offset.
Take two satellites in orbit. Draw an imaginary box around them, and call that your elevator. The satellites are at two distinct altitudes. Are they going to stay in your “elevator”, locked in the same relative positions? Hardly.
There is no difference here in your thought experiment. You and the elevator are two different satellites. Unless you are in the same orbit, your paths are going to diverge.
I dislike it when people who are untutored and unaware of the subject upon which they are pontificating make unsupported assertions based on fallacious mental pictures. I really hate it when they are smug about it. Smug ignorance is what led us to the climate change fiasco. You would be well advised to choose a different path.
clivebest says:
February 23, 2014 at 1:25 pm
“General relativity kind of explains this by explaining that mass/energy distorts space-time. Your lift shaft or free falling object then becomes a geodesic in curved space.”
Yes, and the curvature tensor tells you how neighboring geodesic lines will diverge. According to Willis (and, Leif), spacetime magically flattens in the vicinity of a distributed mass. I feel like I am arguing with cavemen.
Bart says:
February 23, 2014 at 1:43 pm
You make my point perfectly. The difference is the tidal effect, and it exists in Figure 2, nothing to do with centrifugal force.
w.
Bart says:
February 23, 2014 at 1:52 pm
I’ve given you a link to five different mathematical calculations of the tidal force, using five different frames of reference. In every one of them, the centrifugal terms cancel out. I’ve pointed out that you can’t beat math with your mouth, and invited you to show where the math was wrong.
Rather than even attempt that, you just give us more mouth … prate all you want, Bart. Until you can show the math is wrong, you’ve done nothing. Your mouth doesn’t beat the math and never will. So either get onto the math, or shut the mouth—it’s not doing you a bit of good.
I give you math. You give us mouth. Just who is the caveman here?
w.
Willis Eschenbach says:
February 23, 2014 at 6:34 pm
“You make my point perfectly. The difference is the tidal effect, and it exists in Figure 2, nothing to do with centrifugal force.”
You are making my point. Your thought exercise is for two unattached bodies, unconstrained in motion relative to one another. When there is a constraint on how they move with respect to one another, that requires constraint forces, and those constraint forces depend upon the relative centripetal acceleration, as well as gravity.
You have simplified the problem too far. A distributed body is not in free-fall. Only its center of gravity is in free-fall. Every other part of the body is in constrained motion with respect to that point. Otherwise, the component trajectories would diverge based on their relative positions and velocities within the gravity well.
Willis Eschenbach says:
February 23, 2014 at 6:40 pm
“Until you can show the math is wrong, you’ve done nothing.”
Willis, you appear to be operating under a misapprehension of what I have been telling you.
E.g., your link here:
I am in no way suggesting that the second tidal bulge is created by centrifugal “force”. If you look back upthread to my discussion with Steve Fitzpatrick, you will see that I clearly and unequivocally disagree with that statement. I thought that should have been pretty clear by now, but it appears perhaps you missed that discussion.
Since I am not claiming this, your links denouncing those who do are inapplicable.
What I am telling you is that the centripetal acceleration further elongates the bulges. Look again at my comment here, which touched off this argument.The centripetal accelerations add additional terms which create greater tension, resulting in greater bulging on both ends.
Leif claims that this additional term is due to “spin” of the Earth, and therefore should not create any differential bulging. But, what he calls “spin” is measured with respect to a non-inertial frame, so that is an incorrect interpretation. The inertially fixed point is the barycenter of the two body system, and it is with respect to this that you must measure the dynamically important variables. The fact that, in steady state, the differential accelerations at equal radii from the Earth are equivalent from either point of view does not make them equally valid.
For example, suppose we had a space vehicle with four tensile cables with probes mounted at the ends. Something like, maybe, this beast. If the spin rate is greater than the orbit rate, then the probes will extend out due to the centrifugal “force” of the spin. However, at spin rate equal to the orbit rate, we have a resonance condition. If the configuration were initially with one probe extended down, one up, and the other two side to side, the two side to side ones would not stay there, held in place by the putative spin. They would start oscillating and eventually, due to energy dissipation, they would either flop upwards or downwards to lie alongside the radially distributed ones. The CG of the system would continue in orbit without change, but the location of that CG amoung all the bodies would shift. These kinds of dynamics are well known and extensively studied in space physics.
Just so, the centripetal acceleration of the Earth also creates two tidal bulges. Not a uniform displacement, because displacements at the sides would be unstable. These bulges add to the two bulges present due to gravitational forces. I would go further, but detailed explanation of how this happens is rather involved, and I am obviously having enough trouble getting my point across as it is.
Bart:
Do you accept that there is approximately 21 km of bulge created in the rock by Earth’s axial rotation alone?
Do you accept that there is approximately 0.3 m of bulge created in the rock by the Sun and Earth’s axial rotation and orbit?
Do you accept that there is approximately 0.6 m of bulge created in the rock by the Moon and Earth’s axial rotation and orbit?
Do you accept that the bulges caused by Earth’s axial rotation and orbit in the oceans are lower in magnitude than those that occur in the rock?
Do you accept that the orbital changes that modulate the above produce even smaller variations still?
RichardLH says:
February 24, 2014 at 3:56 am
“Do you accept that the orbital changes that modulate the above produce even smaller variations still?”
The contribution of the centripetal acceleration about the Sun to the stress produced along the Sun-Earth line is 50% of that induced by gravity alone. That is non-negligible.
Something which has been missed in all this is that much of this is convention. You can solve for the equipotential surface in either an inertial frame, or in the rotating frame of reference. The latter is, IMO, conceptually simpler, but if done properly, the results should be the same. What I call the effects of centripetal acceleration in the rotating frame can be designated the relative acceleration of the Earth in the inertial frame. Since the centripetal acceleration is a function of the gravitational pull of the Sun, one can make the claim that it is all gravity. All roads lead to Rome, or at least, all good roads lead to Rome.
This tempest in a teapot started when Leif suggested that my equations above were wrong, because I had committed the sin of speaking of centripetal acceleration. It is a sin, because the usual connotation of incorporating fictitious forces into the solution produces the erroneous conclusion that the bulge is two-sided because of the centripetal acceleration. Willis, I think, also believed that was my position, and would have been correct in calling me down upon it if that were, indeed, what I was claiming.
But, my equations are correct, and it is a fully valid way of looking at the problem. It is the standard approach for calculating the tension in the tether for one of these animals. It was, in fact, Leif who was wrong, because he was looking at the Earth as a static reference frame, and his calculation for the delta-specific force was off by a factor of 2/3. I was put off by it because the equations I presented above are so direct and simple, and obviously correct, that if anyone actually took the time to look at it, one should immediately see that they are correct.
In want to post here and will do ASAP but gravity is causing me an issue. Seems CAGW snow has caused a collapse of the roof on the barn.
FWIW the rocky belt would have been caused by a planet/moon system approaching\g from the rear (generally) of the direction of the sun’s travel. change the direction of the force causing a change of the gravitational orbit and BOOM, possibly.
Above comment done in haste. I should have used spell check before posting but long day and another unwanted project due to collapsed roof has my needed attention and will take considerable effort. Lesson learned, if to know you might need a series of tension cables (structurally speaking) in the event of extremely heavy snow but it’s July while you’re building, well don’t let it slip your mind. That heavier than usual winter snow will come even if it takes a few years.
Gravity is a powerful force. Don’t take it lightly.
This thread has really opened my mind to much thought and I look forward to some discussion sometime in the future. Terrestrial gravitational forces are the most pressing need from my view point at this time.
Bart:
“The contribution of the centripetal acceleration about the Sun to the stress produced along the Sun-Earth line is 50% of that induced by gravity alone. That is non-negligible.”
Fact checking the link I have already provided (as have many others)
Tidal trivia.
•Amplitude of gravitational tides in deep mid-ocean: about 1 meter.
•Shoreline tides can be more than 10 times as large as in mid-ocean.
•Amplitude of tides in the Earth’s crust: about 20 cm.
•Ratio of sun/moon tidal forces on Earth is 0.465.
•Angular velocity of Earth’s axial rotation: 7.29 x 10-5 rad/s.
•Angular velocity of moon’s revolution around Earth: 2.67 x 10-6 rad/s.
•Earth polar diameter: 12710 km.
•Earth equatorial diameter: 12756 km.
•Difference between these diameters: 46 km.
•Difference between these radii: 23 km, or 0.4 %.
•Centripetal acceleration at Earth’s surface due to Earth’s axial rotation: 0.034 m/s2
•Size of centripetal acceleration at Earth’s surface due to Earth’s circular motion around the Earth-moon barycenter: 3.3 x 10-5 m/s2.
Add to those
6,378.14 kilometres of rock (average).
3.8 kilometres of water (average)
Centripetal forces
Earth rotation 0.034 m/s^2
Earth orbital round Sun ~0.0000952 m/s^2
Angular velocity of Earth’s axial rotation in radians per second = 7.29 x 10^-5 rad/s
Angular velocity of Earth around the Sun in radians per second = 1.99 × 10^-7 rad/s
Earth’s average orbit of 149.59787 * 10^6 kilometres
Earth’s equatorial radius of 6,378.14 kilometres
“Earth orbital round Sun ~0.0000952 m/s^2”
You’ll want to check that calculation again. Make sure you are using consistent units.
Earth rotation 0.034 m/s^2
Earth orbital round Sun ~0.0000952 m/s^2
Angular velocity of Earth’s axial rotation in radians per second = 7.29 x 10^-5 rad/s
Angular velocity of Earth around the Sun in radians per second = 1.99 × 10^-7 rad/s
As there is a 10^-2 between the two angular velocities I would have thought it was correct. Do you have a different value, and, if so, how did you calculate it?
But, the radius about the Sun is much greater than the radius of the Earth.
Of course, but that makes my point not yours. It is, after all, the difference between a straight line and the curve that is the reason for the Centripetal force. Smaller difference, smaller force.
The next centripetal acceleration down in size is the one I listed above.
Size of centripetal acceleration at Earth’s surface due to Earth’s circular motion around the Earth-moon barycenter: 3.3 x 10-5 m/s2.
Then we get the orbital round the Sun.
I really do not know what point you are trying to make.
Earth orbital round Sun = 149.59787e9*(1.99e-7)^2 = 0.0059 m/s^2
Bart:
So you have the orbital round the Sun centripetal force greater than the size of centripetal force at Earth’s surface due to Earth’s circular motion around the Earth-moon barycenter at 3.3 x 10-5 m/s2?
How do you manage that?
Given that Earth axis rotational centripetal force is 0.034 m/s^2, are you seriously suggesting that the orbital figure is that close to that rotational figure and larger than the barycenter figure? I suspect you have the maths wrong somewhere.
These are deltas against the 9.8 m/s^2 in any case which will triumph in all cases. You can barely detect the difference between being weighed at the poles and the equator. You need a really good set of scales. To detect the differences then added by any barycentre movement and Earth orbital values gets to an even higher degree of precision.
Also you seem to have failed to notice that any such values that do exist will be expressed almost entirely in the rock, the oceans response to all this is even tinier still. 21-23 km (depending on sources) of Earth rotational is in the rock after all. We would still have that oblate spheroid even if there were no oceans at all.
Bart: I apologise – the value you give is correct – the point about it being expressed in the rock stands though. Any water on top of the rock will see very little.
Define “very little”. It is 1/3 of the total solar tidal differential force at the sub-solar point and its antipode.
21-23 km of the Earth’s rotational budget in the rock as against .3m or so in the oceans from the same source. You do the maths for the rest but it is very tiny.
Sorry that should be 0.03 m, I missed a decimal place.
i.e. Earth rotation of 0.034 m/s^2 = 21-23 km in the rock, about 0.03m in the ocean above the rock..
I think you are getting lost in the forest. It is 1/3 of the solar tidal forcing. Not particularly small.
There are certainly effects on ocean dynamics due to the spin of the Earth beyond the orbit rate, but that is another subject entirely.
Look, the only thing I care about here is my statement above. If you have a problem with that, state so and why. Otherwise, you are engaging in discussion with which I am not particularly interested at this time.
Bart:
You obviously have decided you have lost and are walking away.
The majority of the centripetal is in the rock (from what ever source). The Earth Tide is much larger than the Ocean tide (for the same reason).
As I said up thread, there are 6,378.14 km of rock and around 3.4 km of water. Where do you expect the majority of the forces to show up and why?
Please come back with figures that show that to be wrong.
RichardLH says:
February 27, 2014 at 1:55 am
Lost what? I made a correct argument which you and others have in no way impeached. That is all I ever cared about. I’m not interested in further details. I made a statement. The statement was correct. The statement was challenged. The challengers were wrong. That’s it.
Bart:
I too have made an observation which you have very carefully failed to address. The majority of ALL forces show up in distortions in the rock, not the water.
You have not and cannot address that as it throws your whole case into failure.
9.8 m/s^2 triumphs and the rest is barely able to raise a ripple. The main centripetal rotational figure causes the largest outcome and that is most definitely in the rock. Then we have the two tides, again mainly in the rock. Then somewhere down in the dust we have whatever other forces you believe are important as very tiny modifiers of those. And, again, most of those show up in the rock.
Until you come to terms with that state of affairs you are most definitely lost.
Bart,
You are obviously very intelligent as you have made quite detailed arguments trying to support your view. If I may suggest, go back to the beginning of this thread and follow my comments and the responses/comments to those comments by others. Watch my learning curve however vaguely presented.
Now try my simple thought experiment as noted in comment ” eyesonu says: February 21, 2014 at 10:59 am”.
Follow the remaining comments by me. A lot of warts in my presentation (to say the least) but It was quite an eye-opener when I grasped what Willis and Leif had presented.
To follow/interpret what I offered would take much less of your time than many of your arguments. I understand your reason for your arguments as that point of view is where I started out.
Note that I am here on WUWT as my only motivation is to understand things presented here. If I had more time and motivation I could have been much better with the written composition of my comments. But then keep in mind that I’m just a country bumpkin.
Just trying to help as it is clear that you have an interest. This thread is now two weeks old and almost 500 comments. No one would still be here if not interested. Hope this helps.
RichardLH says:
February 28, 2014 at 2:26 am
“I too have made an observation which you have very carefully failed to address.”
Don’t be paranoid. I have very uncarefully failed to address it. I do not know if you are wrong or right. I do not even know specifically what you are arguing, and have no real desire to know. I have been focused on showing that my argument above is correct. It is. That is all I care about. If you want to engage on that topic, I can oblige. If not, you should probably find someone else to argue with. This entire thread is going to expire any day or moment now, and there is no time to get involved in a protracted additional discussion anyway.
eyesonu says:
February 28, 2014 at 7:22 am
Thank you for your concern, but please take my word for it that I have actual, real world experience with these things, and know very well of what I speak. Better than these other guys do. If you find yourself disagreeing with me, then you are either A) correct, and there exists a 1:1 mapping with what I am saying so that we are actually both correct or B) wrong.
The fundamental thing people have got wrong, it seems, is in assuming the entire Earth is in free fall about the Sun. It isn’t. Only the center of gravity is in free fall. The rest of the body is being pulled along for the ride, and this creates internal stresses.
It is the same with your three-mass problem. The center of gravity of the three masses together is in free fall, but individually, they are not. Each mass is carving out its own trajectory in space and time relative to that center of gravity. They are not being equally pulled by gravity, and they are not uniformly accelerating through space.
Bart says:
February 28, 2014 at 9:35 am
“…. please take my word for it that I have actual, real world experience with these things, and know very well of what I speak. Better than these other guys do ….”
=================
I believe I understand clearly now.
eyesonu says:
February 28, 2014 at 11:17 am
—————————————-
Great thread. I see that this is a save for future study thread. I,m glad I noticed your last post. By the way, Bart,s last comment is very interesting.
On another note, when I moved into the mountains in the early 70s, I became very good at making hasenpfeffer.