By Dr. Sebastian Lüning, Prof. Fritz Vahrenholt and Pierre Gosselin
One of the main points of criticism of the CO2-dominated climate models is that they fail to reproduce the temperature fluctuations over the last 10,000 years. This surprises no one as these models assign scant climate impact to major factors, i.e. the sun. As numerous IPCC-ignored studies show, the post-Ice Age temperature curve for the most part ran synchronously with solar activity fluctuations. The obvious discrepancy between modeled theory and measured reality has been brought up time and again.
The journal Climate of the Past Discussions has published a new paper written by a team led by Gerrit Lohmann of the Alfred Wegener Institute (AWI) in Bremerhaven, Germany. The group compared geologically reconstructed ocean-temperature data over the last 6000 years to results from modeling. If the models were indeed reliable, as is often claimed, then there would be good agreement. Unfortunately in Lohmann’s case, agreement was non-existent.
Lohmann et al plotted the geologically reconstructed temperatures and compared them to modeled temperature curves from the ECHO-G Model. What did they find? The modeled trends underestimated the geologically reconstructed temperature trend by a factor of two to five. Other scientists have come up with similar results (e.g. Lorenz et al. 2006, Brewer et al. 2007, Schneider et al. 2010).
The comprehensive temperature data collection of the Lohmann team distinctly shows the characteristic millennial scale temperature cycle for many regions investigated, see Figure 1 below. Temperatures fluctuated rhythmically over a range of one to three degrees Celsius. In many cases these are suspected to be solar-synchronous cycles, like the ones American Gerard Bond successfully showed using sediment cores from the North Atlantic more than 10 years ago. And here’s an even more astonishing observation: In more than half of the regions investigated, temperatures have actually fallen over the last 6000 years.
Figure 1: Temperature reconstructions based on Mg/Ca method and trends with error bars. From Lohmann et al. (2012).
What can we conclude from all this? Obviously the models do not even come close to properly reproducing the reconstructed temperatures of the past. This brings us to a fork in the road, with each path leading to a completely different destination: 1) geologists would likely trust their temperatures and have doubts concerning the reliability of the climate model. Or 2) mathematicians and physicists think the reconstructions are wrong and their models correct. The latter is the view that the Lohmann troop is initially leaning to. We have to point out that Gerrit Lohmann studied mathematics and physics, and is not a geo-scientist. Lohmann et al prefer to conjure thoughts on whether the dynamics between ocean conditions and the organisms could have falsified the temperature reconstructions, and so they conclude:
“These findings challenge the quantitative comparability of climate model sensitivity and reconstructed temperature trends from proxy data.“
Now comes the unexpected. The scientists then contemplate out loud if perhaps the long-term climate sensitivity has been set too low. In this case additional positive feedback mechanisms would have to be assumed. A higher climate sensitivity would then amplify the Milankovitch cyclic to the extent that the observed discrepancy would disappear, this according to Lohmann and colleagues. If this were the case, then one would have to calculate an even higher climate sensitivity for CO2 as well, which on a century-scale would produce an even higher future warming than what has been assumed by the IPCC up to now. An amazing interpretation.
The thought that the climate model might be fundamentally faulty regarding the weighting of individual climate factors does not even occur to Lohmann. There’s a lot that indicates that some important factors have been completely under-estimated (e.g. sun) and other climate factors have been grossly over-estimated (e.g. CO2). Indeed the word “solar” is not mentioned once in the entire paper.
So where does their thought-blockage come from? For one it is a fact that physicist Lohmann comes from the modeling side, and stands firmly behind the CO2-centred IPCC climate models. In their introduction Lohmann & colleagues write:
“Numerical climate models are clearly unequalled in their ability to simulate a broad suite of phenomena in the climate system […]“
Lohmann’s priorities are made clear already in the very first sentence of their paper:
“A serious problem of future environmental conditions is how increasing human industrialisation with growing emissions of greenhouse gases will induce a significant impact on the Earth’s climate.”
Here Lohmann makes it clear that alternative interpretations are excluded. This is hardly the scientific approach. A look at Lohmann’s resume sheds more light on how he thinks. From 1996 to 2000 Lohmann worked at the Max Planck Institute for Meteorology in Hamburg with warmists Klaus Hasselmann and Mojib Latif, both of whom feel very much at home at the IPCC. So in the end what we have here is a paper whose science proposes using modeled theory to dismiss real, observed data. Science turned on its head.
[Added: “SL wants to apologize to the authors of the discussed article for the lack of scientific preciseness in the retracted sentences.” ]
From 1996 to 2000 Lohmann worked at the Max Planck Institute for Meteorology in Hamburg with warmists Klaus Hasselmann and Mojib Latif, both of whom feel very much at home at the IPCC.
[Note the above text was changed on 4/16/12 at 130PM PST as the request of Dr. Sebastian Lüning – Anthony]
The model must be wrong them.
Keep trying.
Since Lohmann et al are already convinced they know the answer to climate change, its causes and its effects, it is clear that the sole reason for trying to make the stupid models echo their beliefs is for nothing other than propaganda reasons. Sorry for stating the obvious.
I would call Lohmann an amateur modeler and a True Believer. He should spend some time with meteorologists.
I am not one but I can use google:
Search for “Convection parameterization”. A goldmine. An example:
http://www.met.tamu.edu/class/metr452/models/2001/convection.html
“Just as all people have unique skills and abilities, the convective parameterization schemes of the various models will do different things well and different things poorly. Often, the skill of the model depends on the exact location and time for which it is forecasting. For example, the AVN under predicts mesoscale convective events across the Great Plains during the warmest part of the year. The ETA parameterizes convection differently over water than land, thus it often overestimates precipitation along the Gulf and Atlantic coasts. The ETA is also plagued by a greater amount of convective feedback than the NGM. The MRF now accounts for factors such as evaporation of falling rain like the RUC and NGM. […]”
“This brings us to a fork in the road, with each path leading to a completely different destination: 1) geologists would likely trust their temperatures and have doubts concerning the reliability of the climate model. Or 2) mathematicians and physicists think the reconstructions are wrong and their models correct.”
Classic ‘climate science’ in action – nothing else needs to be said.
But how do we know what climate was 6,000 years ago? I thought paleoclimate reconstructions were all proxy-pseudo science?
This is an unjustified generalisation. Often it is mathematicians who are the most sceptical about the accuracy of these models because they are the ones with the greatest appreciation of the difficulties involved.
“Science turned on it’s head”. Any similarity to the Jesuit defence of a universe centred on a flat Earth, including the use of an Inquisition to convince sceptics of the error of their ways, is entirely in the mind of the observer.
I’ve never understood why so many on both sides of the climate debate seem to think that climate sensitivity is static, i.e. that the feedback effects to warming (like incresed CO2, changes to albedo, ect.) are the same at every level of Global Tempurature. I would assume just the opposite, that the effect of a change in one forceing during an Ice Age could be vary different then the same change made during an Interglacial.
There is a popular phrase that neatly describes the state of being so absorbed in one’s own constructions that one’s direct view of external reality is occluded.
Eklund says:
April 15, 2012 at 12:25 pm
“But how do we know what climate was 6,000 years ago? I thought paleoclimate reconstructions were all proxy-pseudo science?”
Eklund, you should read your link before making assumptions. Pat Frank thoroughly explains the difference between scientific proxies and pseudo-scientific proxies.
I decided to read the full article.
Basically, it is a bunch of guys flailing around in a futile attempt to try and find desperate excuses why their models don’t match the realities of observed data. Bottom line: The data has to be wrong.
Anyhow, it is funded: “within the priority programme Interdynamik of the German Science Foundation (DFG).” So it’s just another case of grant addiction BS.
the computer models don’t fit recorded historical data because they are written to forcast future climate. has anyone considered using the historical data as the basis for a computer program to reflect that data and to form the basis to predict future climate?? seems to me it would be more accurate than the garbage being used today
Well written, Anthony. The surprise ending was hilarious. That which is assumed, no matter how unlikely, must be true.
A classic exmaple of the first rule of clmate science , if the model and reality differ in value its reality which is wrong.
Classic pathological science.
http://thepointman.wordpress.com/2011/10/14/global-warming-and-pathological-science/
Pointman
Schitzree says:
April 15, 2012 at 12:30 pm
“I’ve never understood why so many on both sides of the climate debate seem to think that climate sensitivity is static, i.e. that the feedback effects to warming (like incresed CO2, changes to albedo, ect.) are the same at every level of Global Tempurature. I would assume just the opposite, that the effect of a change in one forceing during an Ice Age could be vary different then the same change made during an Interglacial.”
Schitzree, what you’re describing is a nonlinear feedback, and everyone agrees that at least some of the feedbacks are nonlinear, starting with the “default negative feedback” that even the most hardline warmists don’t deny, the blackbody or graybody radiation of the surface that is described by the Stefan-Boltzmann Law, and is proportional to the 4th power of the absolute temperature; so it is non-linear.
The fundamental error in all models and here again, is that they assume that every change of 1 W/m2 is the same, whatever the source. As if 1 W/m2 change in solar (specifically in the UV spectrum in the stratosphere on ozone) has the same effect as 1 W/m2 change in IR by CO2 in the lower troposphere.
Nobody who ever worked with a real process in the real world would assume such a thing, but that is exactly what happens with the climate models…
but, but, but…
Have they tried an ensemble of models?
You know, even if all models are wrong, maybe the ensemble is right.
/sarc
xtron says:
April 15, 2012 at 12:59 pm
“the computer models don’t fit recorded historical data because they are written to forcast future climate. has anyone considered using the historical data as the basis for a computer program to reflect that data and to form the basis to predict future climate?? seems to me it would be more accurate than the garbage being used today”
The GCM’s are tested using the instrument record of global temperatures. Now, they don’t perform well with that, especially given the fact that they are designed to deliver the catastrophic warming in 2100 that the IPCC demands and that the first-stage-thinker physicists like Lohmann expect. They get it roughly right; the rest is papered over by assuming a history of aerosol forcing that explains the deviation.
“Aerosols and “cloud lifetime effect” cited as “enormous uncertainty” in global radiation balance”
http://wattsupwiththat.com/2009/10/06/aerosols-and-cloud-lifetime-effect-cited-as-enormous-uncertainty-in-global-radiation-balance/
…they actually USE this uncertainty to “fix” the half-broken hindcasting of the models in the test runs…
AnonyMoose says:
April 15, 2012 at 1:01 pm
“Well written, Anthony. The surprise ending was hilarious. That which is assumed, no matter how unlikely, must be true.”
The compliment should go to Pierre Gosselin, who translated for Vahrenholt and Lüning, I assume… and runs his own blog,
http://notrickszone.com/
REPLY: True, I didn’t write it, nor translate it. The kudos go to them not me – Anthony
I’ve been in the den of the lion. In a previous life I was responsible for a visualization product which could get virtually arbitrarily dense pixel resolution provided the data was there. In pitching the system to MPI and KRZH, we adjourned to lunch. I made the palpable mistake of asking how good their resolution was on atmospheric phenomena – “For paleo-reconstructions we can do cubes 100 Km on a side.” I bit my tongue and finished my lunch.
They didn’t buy the supercomputer from us, but they did buy my viz product. Now they can see their fantasies in UEBER RESOLUTION. Not much science though…
Lohmann & colleagues write: “Numerical climate models are clearly unequalled in their ability to simulate a broad suite of phenomena in the climate system […]“
——————-
Sure Lohman, but your problem is that your simulations do not agree with the observed facts so your simulations are just fantasies. When did you forget this basic rule for scientists?
Clearly Lohman fails due to his own cognitive biases which he allows to get in the way of considering all the possibilities. He really should consider handing in his doctorate and hanging up his hat as he is not well suited to a career in science.
People like Lohman are not scientists. They are technical hacks who lack the critical thinking skills needed to be real scientists.
Eklund says: “But how do we know what climate was 6,000 years ago? I thought paleoclimate reconstructions were all proxy-pseudo science?”
Thanks for the great link, Eklund. It was fascinating, well written, and another nail in the coffin of AGW (as if we needed any more). Pity you didn’t read it all the way to the end. Oh, you just read the headline? That would explain it.
Yesterday this site noted that all of the Hadley predictions and proclamations were available for a retroactive review of accuracy;http://wattsupwiththat.com/2012/04/14/met-office-coping-to-predictions/
I note that in COP4, Hadley states unequivocally that its models are accurate in a 6,000 year retrospective model. Because these a re PDFs, I cannot copy the paragraph, but it is on page 4 and entitled Uncertainty In Climate Change Predictions.
http://wattsupwiththat.files.wordpress.com/2012/04/cop4.pdf
On the whole climate sensitivity thing. The modellers appear to rely on correlation between Antarctic temperature and CO2 implying cause and effect in order to diagnose the overall sensitivity. But what if the temperature fluctuations in the Arctic and Antarctic are caused almost entirely by changes the North to South rates of heat/energy flow (equator to pole) rather than by the local effects of greenhouse gases? If that is the case then the whole climate sensitivity argument is turned on its head.
If the annual mean temperature changes at the Vostok core site (for instance) result from hemispheric scale changes in equator to pole insolation gradients then the role for greenhouse gases is reduced and there is no need to invoke outrageous amounts of positive feedback.
But if the proxies are infact wrong, than the climate models are also wrong, as they cannot be validated!
Knowing what the climate was like 6,000 years ago is reasonably easy in lakes and peat bogs.We have good pollen records showing which plant species were abundant, we know the ecology they thrive in, we have 14C timing data and 18O temperature proxies.
http://epic.awi.de/3071/1/Tar1999a.pdf
Bit warmer in the summer and winter in NW Europe than now.
Re
Pointman says:
@ April 15, 2012 at 1:05 pm
That’s a great piece, Pointman.
This is a hard one. Models don’t agree with the proxies, so are the models wrong, or are the proxies wrong, or are they both wrong? Most of us know that proxies are always right and neither are model, so how do we know which is better?
John Penhallurick says:
This is just another nail in the coffin of climate models. Read on –
Flaws in Climate Models
All the predictions of catastrophic effects because of the increase in human emissions of CO2 stem from climate models. For IPCC supporters, these seem to have the same infallibility as if their results had been brought down from Mt Sinai, engraved in stone by the finger of God! But even supporters of climate models are aware that such is not the case. As pointed out in a recent article in the New Scientist of 27 January, 2011, “Casting a critical eye on climate models”, the author, Anil Ananthaswamy, stated: “Our knowledge about the Earth is not perfect, so our models cannot be perfect. And even if we had perfect models, we wouldn’t have the computing resources needed to run the staggeringly complex simulations that would be accurate to the tiniest details.”
He also stated: “There are important phenomena missing from the IPCC’s most recent report. Consider a region that starts warming. This causes the vegetation to die out, leading to desertification and an increase in dust in the atmosphere. Wind transports the dust and deposits it over the ocean, where it acts as fertiliser for plankton. The plankton grow, taking up CO2 from the atmosphere and also emitting dimethyl sulphide, an aerosol that helps form brighter and more reflective clouds, which help cool the atmosphere. This process involves carbon flow, aerosols, temperature changes, and so on, but all in specific ways not accounted for by each factor alone.”
Climate models are deterministic: that is, every factor that is known to influence climate significantly must be included in order for the model to be able to predict a future climate state. But some climate processes are too complex or small in scale to be properly represented in the models; or scientists know too little about the processes in question. These include atmospheric convection; land surface processes such a reflectivity and hydrology; and cloud cover and its microphysics. Modelers parametise these factors: that is, they make guesses about their values. Depending on the values selected, they could make the model show no warming; or very large increases in warming, which would strain credulity. Unsurprisingly, the modelers have chosen values which produce a mild warming, in order to seem more credible. But these values are largely arbitrary.
Another supporter of the climate models pointed out that it is incorrect to say that the models offer predictions; as they are too simplified for that. What they offer are “scenarios”. It is the climate models alone that suggest such devastating effects of human emissions of CO2. Critical to this is estimates of how long CO2 persists in the atmosphere. The IPCC assumes that carbon can persist in the atmosphere for more than a hundred years. This assumption is built into the equations in the models, and the output of the model is determined by these equations. But as is well known, GIGO i. e. garbage in = garbage out.
Is carbon dioxide a threat?
The atmosphere contains about 780 Gigatonnes (Gt) of CO2 (0.039% of the whole atmosphere) of which about 90 Gt are exchanged with the ocean every year and another 120 Gt with plants. Thus about 25% of CO2 is turned over every year. The observed decrease in radioactive C14 after the cessation of atmospheric testing of nuclear weapons confirms that the half-life of CO2 in the atmosphere is less than 10 years. Another source of error in the IPCC’s alarmist forecasts is that climate models ignore the huge amounts of CO2 emitted by volcanoes and particularly submarine volcanoes. Given that the estimate of human production of CO2 is about 7.2 Gt per year (IPCC 2007), Canadian climatologist Timothy Ball (2008) has estimated that this figure is more than four times less than the combined error (32 Gt) on the estimated CO2 production from all other sources.
A still further important factor is the fact that the climate models and the IPCC ignore the fact that the contribution of greenhouse gases is not linear. In fact, as extra gas is added to the atmosphere, incremental temperature increases occur in a declining logarithmic fashion, as can be seen in Figure 2. What this graph suggests is borne out more strongly by data in graphs going back 800 million years: namely that the planet today is in a state of CO2 starvation. The models used by the IPCC predict temperature increases for a doubling of CO2 of 6.4°C (IPCC, 2001) or 4.5°C (IPCC, 2007). The IPCC’s calculations selectively make use of positive feedback effects that further increase temperature, while ignoring negative feedback loops that act to reduce temperature, such as the generation of additional cloud cover, which reflects incoming solar radiation back to space. But even if we assume that the 100 parts per million (ppm) post-industrial increase in CO2 from about 280 ppm to 380 ppm must therefore have already caused most of the anticipated 1.2°C, the negative logarithmic progression of
Figure 2
Taken from Carpenter (2010) p.76.
greenhouse gases means that another increase of 100 ppm would result in only a few tenths of a degree of additional warming.
Figure 3 shows different projections for the amount of warming by 2100. The research papers by independent scientists, which are largely based on observational evidence, predict that if current levels of human emissions continue, the temperature should increase by 0.6°C to 1.2°C. Even from recent evidence, the increase in CO2 does not show a close correlation with any increase in temperature, as can be seen from Figure 4. Temperature fell between 1940 and 1975, while CO2 shows a striking increase.
Also, it must be pointed out that because of the well-known urban heat-island effect, official thermometer readings are highly suspect. For countries including the United States, Australia and New Zealand, temperature measurements from a sample of rural stations reveal no statistically significant warming during the twentieth century. In response to the urban heat-island effect, the temperature responses have been “corrected” by the warmists. But meteorologists Joseph D’Aleo and Anthony Watts in their 2010 paper “Surface Temperature Records: Policy-Driven Deception” stated that instrumental temperature data for the pre-satellite era have been so widely, systematically and undirectionally tampered with that it cannot be credibly asserted that there has been any significant ‘global warming’ in the twentieth century.
Figure 3
Based on Fig. 16 from Carpenter (2010)
Some warmists actually rejoiced when the UAH figure for 2010 came in at 0.54°C, as if this vindicated their views. The Government’s former climate minister, Senator Penny Wong, recently stated (The Australian, 2 Feb. 2010): “Globally 14 of the 15 warmest years on record occurred between 1995 and 2009.” The research papers by independent scientists, which are largely based on observational evidence, predict that if current levels of human emissions continue, the temperature should increase by 0.6°C to 1.2°C. Even from recent evidence, the increase in CO2 does not show a close correlation with any increase in temperature, as can be seen from Figure 4. Temperature fell between 1940 and 1975, while CO2 shows a striking increase.
Since direct temperature records date from only about 1850, and since during that period we have been in a recovery from the Little Ice Age, this is nothing to marvel at. We should also take into account that in that 15-year period, there have been two strong El Nino events (1997 and 2009), and one moderate (2002). The 2009 event does much to explain the large increase in 2010. In contrast, during the same period, there were only three moderate La Nina Events (1999, 2007 and late 2010). The floods in Eastern Australia during early 2011 indicated that the La Nina cycle has strengthened, and we can expect a decrease in the earth’s mean temperature when the data for 2011 are in.
Figure 4
Comparison of temperature increases (determined by Hadley Climate Centre) and CO2 (Taken from Carpenter (2010), Fig. 10.
More fundamentally, the suggestion that meaningful judgements about climate change can be made on the basis of a single year, or even the 150 years since instrumental recordings of temperature began, is laughable. Capenter (2010: 38-69) explains the need to work in terms of climate points, based on 30 year averages. Even the 150 years of instrumental temperatuture measures represents only five climate points, and such intervals are too short to carry statistical significance for long-term climate change. Nonetheless, the warming that has been observed since the last severe stages of the Little Ice Age is likely to be followed like its predecessors, the Roman Warming and the Early Medieval Warming, by cooling, which some meaurements, such as the microwave sounding units borne on NOAA polar orbiting satellites (MSUs), has already started. It is also true that the temperatures we are experiencing around the transition from the twentieth to the twenty-first centuries are not unusually warm, in terms of past climate measurements. They are about one degree C cooler than those that obtained in the Holocene Climate Optima several thousand years ago; about 2° C cooler than those reached in the last interglacial period (125,000 years ago); and about 2°-3° C then those that prevailed in the Pliocene age (6-3 million years ago).
“Or 2) mathematicians and physicists think the reconstructions are wrong and their models correct.”
How can any reasonable, honest person deny the real data and trust in models that go against reality. This is great for fantasy games but not acceptable when your are supposed to be predicting the future.
Believing models despite its divergence from reality is DELUSIONAL. NOTHING LESS.
Eklund says:
April 15, 2012 at 12:25 pm
> But how do we know what climate was 6,000 years ago? I thought paleoclimate reconstructions were all proxy-pseudo science?
We know that in some parts of the world trees were growing like mad in places where today glaciers are retreating and exposing them, or at least those brought downhill during a glacial advance since then.
After hearing a couple stories one week, I created http://wermenh.com/climate/6000.html
“Numerical climate models are clearly unequalled in their ability to simulate a broad suite of phenomena in the climate system […]“
Isn’t that just plain circular reasoning? What else simulates phenomomena beside a numerical model? Are there non-numerical models that produce simulated values for measureable climate/weather phenomena? Isn’t that a bit like saying “numerical climate models are much better than studying teas leaves to simulate the climate”? Of course, unequalled does not mean perfect, just better than the others. That unequalled could still be quite useless, particular for predictive uses.
What kind of computer “model” can’t reproduce it’s own “training data” ?
The only answer that comes to mind … a POS.
What about this possibility? That both the geological reconstructions and the mathematical climate models are wrong? What a conundrum that would create for everybody. Perhaps, however, that IS really the case. Maybe we don’t know, and will never know, with any reasonable certainty exactly what the temperature WAS a long time ago. Which is why I’ve been saying for some time that this subject of climate needs a LOT more study than it has been given, up until recently. We are still in the throes of a nascent area of science.
Tiresome, really, to endlessly rebut GCM poltroons on their peculiar prejudices. As if any of them appreciate the difference between fantasy and reality, or even –frankly– care.
The Warmistas never bother to match the information content of their models next to that of the Earth’s climate system. How many meaningfully distinct pixels are there on the Earth’s surface, and how many air-voxels do we store above each one, and sea-voxels for water-surface? Then how many bits per pixel & voxel, to capture the atmosphere’s information?
Let’s start with a square meter, of which the Earth has 5.1E14. Surface spectral characteristics, thermal properties, and moisture content, among others information, make for numerous bits per pixel, and I’ll try 1,000 bits for starters.
Above each pixel stack 1999 voxels, expanding in size as you go up into the stratosphere. For all those voxels we want temperature, presssure, humidity, velocity, turbulence state, aerosol number spectrum and chemical content, and absorption spectrum both visible & thermal. Again, 1000 bits per voxel.
Our grand total 1E22 bits, or 10 billion terabytes for surface & air, before accounting for all the bodies of water too. Interpixel correlations will of course help reduce the load, but the bit count goes back up as soon as you include all the complexities discussed at WUWT.
Sorry, 100-km grid cells and amateurish ‘parameterizations’ are far below the Apocalypse-Grade of quality they blithely assume their simulations deserve. Come back in 30 years when computers are a million times better than today, and the atmosphere and oceans swarm with sensors, and a fleet of high-resolution hyperspectral satellite-scopes orbits overhead everywhere. But with that much knowledge, geoengineering would be millions of times cheaper than shutting down civilization.
Isn’t the earth’s atmosphere-ocean, convection-radiation thermodynamic system, a stochastic-chaotic relationship? Isn’t it true that such a system cannot be predicted with any certainty?
Doesn’t a 6,000 year or 2,160,000 day simulation have error bars that make the exercise even more completely futile?
Why are “scientist’s” running 2 million day weather forecasts of un-forecastable entities? Oh, I forgot, for the money… right, who cares about Truth, Justice & The American Way… or The Scientific Method!
If the models are wrong, lets just get a new model. Claudia Schiffer, Kathy Ireland, Kate Moss, etc. See, there are plenty of models to chose from!
/Cheap Humor…
Oh, sweet–next time the weather is bad, or the termperature is hot, or too cold, we can all ignore this “data”–it wasn’t modeled.
Problem with “climate” is solved. (Now where’s my COP list of objectives and my Agenda 21 specifications?)
We are seeing such things more often recently. This is what happens when “the wheels come off”
a scientific orthodozy. Expect to see the level of riduculousness increase as band-aid after band-aid is invented to “explain” new observations, whilst preserving the the ortodox belief system. The same thing happened in astronomy in the Copernicus’s time.
No one even knows all inputs to climate.
My weather rock never fails: wet-raining, gone-tornado. I live in East Texas, so that’s about the only exercise it gets!
These folks and their GCMs are simply delusional. Anyone watching the Weather Channel over the past few days surely must realize weather is a chaotic system, we DO NOT understand all (any?) of the parameters which drive it and the GCMs are simply a different way to spell GIGO!
Urederra says:
April 15, 2012 at 1:12 pm
but, but, but…
Have they tried an ensemble of models?
You know, even if all models are wrong, maybe the ensemble is right.
/sarc
And it’ll probably be right twice a day, too!
Ummmm — whut?
@ Bill Tuttle. I believe there’s a formula for this: n(chimp+typewriter) = Hamlet.
grumpyoldmanuk says:
April 15, 2012 at 11:55 pm
@ Bill Tuttle. I believe there’s a formula for this: n(chimp+typewriter) = Hamlet.
With the warmies, the formula results in “As You Like It”…
I am a physicist, and I don’t like the implication that all physicists will take a model veracity over properly measured actual data. As I physicist I realize that the most important observations are those that the current theory can’t explain as this is how the real breakthroughs in science are made.
My main concern with what the current climate science establishment is doing is, aside from the huge bill we all face and the environmental damage they are causing, is the damage they are doing to science, real observational based science. there seems to be a generation of scientists out there who do not have a clue about the fundamental scientific method and do nothing but play with numbers.
The comments ion this post just illustrate how much damage they are doing to the reputation of proper physical science. I would love to hear what Feynman would have to say about all this!
This surprises no one as these models assign scant climate impact to major factors, i.e. the sun.
———-
I don’t buy that.
I suspect strongly that the insolation physics is in the models, but the insolation varies so little that for the here and now it’s not relatable to current temperature changes.
You can wave your hands about madly over other postulated solar influences, but they are unproven and are not even quantified or describable with math.
Ian H says:
, idealizes Newton’s Law of Gravitation as near-Earth gravity (and the latter idealizes some sort of quantum theory of gravitation and/or curve space theories of gravitation that we do not fully understand and cannot currently reconcile). Using 
as a force acting on a falling object idealizes away drag forces, frictional forces, ignores the fact that the frame of reference where observations are made is not really inertial. And that’s just the beginning — dropping a mass off of a tower — in a long line of idealizations, of toy models, of things that work well enough up to a point and then fail (sometimes major fail). Actually, the mass approaches terminal velocity. Actually, no it doesn’t, not if it is irregularly shaped and tumbles. No, not even that is correct when one takes into account the blowing of the wind.In the end, if the mass is a wadded piece of paper and the tower is my hand held two meters over the ground outside (where it is a fairly gusty day, according to my wind-chimes in the back yard)
April 15, 2012 at 12:27 pm
mathematicians and physicists think the reconstructions are wrong and their models correct.
This is an unjustified generalisation. Often it is mathematicians who are the most sceptical about the accuracy of these models because they are the ones with the greatest appreciation of the difficulties involved.
Speaking as a person who is both and who has done a ton of modelling, this is absolutely correct. Most physics computations are done using what I would call a “toy model” — an idealization of the true physics that ignores or neglects many things. As a consequence, they don’t usually get the right answers, not really, not unless they include heuristic or semi-empirical terms and even then only over a limited range.
One doesn’t have to go far to find such things as toy models — if you visit my online intro physics textbook, nearly all of its content consists of just such idealizations. In a sense, physics is a big collection of toy models, all of them imperfect and provisional (but useful in some regime).
In the very first pages of introductory mechanics, Newton’s Laws idealize relativistic quantum field mechanics in the large, slowly moving regime. The first force law one learns,
The modeled trends underestimated the geologically reconstructed temperature trend by a factor of two to five.
———–
Well that’s interesting. So how does this model compare to the others?
Is it an old model? Older models have more semi empirical relationships built, in while newer models use more an initio calculations. This means that the newer models behave better over a wider range of physical conditions.
Went looking
Rather than “models” we have the one model: ECHO-G. This is described here: http://www-pcmdi.llnl.gov/ipcc/model_documentation/ECHO-G.pdf
It is a 2001 vintage model and used as one input for AR4. In short quite old.
Don’t know how it compares to others leaving open the question of whether this model typically underestimates temperatures.
From the paper abstract
“Alkenone-based SST records show a similar pattern as the simulated annual mean SSTs, but the simulated SST trends underestimate the alkenone-based SST trends by a factor of two to five. ”
So I think this is interpreted as the alkenone and model values match, except for a wobbly scaling factor, but the Mg/Ca ratio values do not. This also implies that the Mg/Ca values do not match the alkenone values.
The proxies do not agree with each other. So it could in fact be plausible that the Mg/Ca proxies are measuring something else and the modelling is not as bad as represented above.
Probably need to look at the paper and not just the abstract.
RHS says:
April 15, 2012 at 9:24 pm
If the models are wrong, lets just get a new model. Claudia Schiffer, Kathy Ireland, Kate Moss, etc. See, there are plenty of models to chose from!
/Cheap Humor…
I can’t afford a new model; I am paying for new windmills.
Wow. That was a good one. Double interface error. The formula was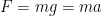
only F, g and a were vectors. And I have no idea why the thing posted as it did so in mid typing stream as I hit enter to start a newline. Oh, well.
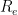to the acceleration of the moon in a circular orbit of radius 
and discovered that they were in the ratio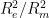 
.
…according to my wind-chimes in the back yard) it is basically impossible to predict the precise motion of that piece of paper. If one drops it many times, one drop might go straight down, the next it might be blown two meters laterally on the way down. Yet I teach Newton’s Laws and gravitation, and believe them to be true in context and useful as well. It’s just a mistake to think that the simple model is really adequate to predict a much more complex reality.
Models are therefore enormously useful. On the one hand, they give us a quick and dirty way to predict and understand reality, one that often works pretty well in spite of the idealizations. On the other, where they fail it is a clear sign that there is more going on than is included in the models. If one drops a round smooth marble a thousand times and carefully record its position as a function of time, analysis of the motion and comparison with the model of uniform gravity might permit you to infer linear (and or nonlinear) drag forces! A failed model teaches us things!
Or sometimes, it works the other way. A simple model is “suddenly” seen to be a special case of a more general model that has greater explanatory power. Newton’s discovery of gravitation worked like that — he compared the acceleration of his apple at the earth’s surface at radius
It is sad, though, when a physicist or mathematician believes in their toy model so much that they forget that it is a toy, or worse, forget that in the end the model must be compared to reality or else you will not ever learn where your model fails, where some key piece of physics you ignored in your idealization turns out not to be ignorable. It is even worse when a piece of supposed science is prefaced with social platitudes explaining how the work will help save the planet from evil instead of simply presenting the data, the analysis, and the results without making the claim that the models are correct and it is the data that must be at fault. That’s simply absurd.
So sad. Anthony summarizes the paper so succinctly above — climate models cannot reproduce the proxy-derived geothermal history of the planet. Forget 6000 years — they cannot reproduce it on any significant timescale. It would have sufficed for them to have simply presented the data, the computation, noted that the latter doesn’t fit the former and stopped. It would have been reasonable to assert that the failure implies a probable failure of the toy model (given their many other failings on shorter timescales than this). But to assert that the data must be incorrect because the toy model is correct is simply laughable.
BTW, regular readers who have been following the other threads will be pleased by my report on the Durham weather yesterday. The NWS was predicting a high of 91F and a low of 61F. When I woke up, the low Sunday morning was round 57F. The 24 hour high recorded by my thermometer outside was 82F, and that was for around a five minute window when the sun was actually on the thermometer housing (I don’t have a big fancy fan-blowing weather station, only a simple hanging wireless thermometer located arguably too close to the house on the northeast side). The air temperature on that side of the house — with a steady breeze blowing all day — probably never exceeded 81F.
Again, people almost never actually check the NWS forecast against reality — their perception of the day’s temperatures is what they were forecast to be as they were in an office or indoors most of the day and never actually experienced the temperature outdoors in the warmest part of the day.
10F is an enormous error. They’re calling for 91 again today and tomorrow. Today I might believe it — it is 71 and quite sunny, and if the humidity climbs just right it could warm up (humid air but no clouds). OTOH, if it clouds up as it is supposed to, 91 is perhaps dubious. Still, I would be very interested in seeing whether or not the mean error in NWS forecasts for high and low temperatures have a systematic error on the warm side, on average. What a sublime way to “subtly” create the perception of warming in a society that is largely out of touch with the outdoors, living in air-conditioned environments! The prediction is the reality!
Sadly, I have no real data on this — it is just anecdotal. It seems to me that the NWS forecast here errs far more often on the warm side than on the cool side. In fact, it hardly ever errs on the cool side, predicts a high or low temperature that is too low. Could a “warming bias” have crept somehow into the NWS computers? Do they not have any sort of feedback loop that simply increments or decrements a correction factor empirically to maintain a mean error of zero? Or is their output the result of running climate models that at this point are hopelessly biased on the warming side (and nobody is checking to notice this)?
rgb
BTW, is everybody else seeing all posts in italics, or is it just my browser? 1/3 of the way through my first post above (at the point it went in spontaneously without my clicking post comment) italics turned on and now everybody’s posts appear to be in italics, but only from that point on. Sigh.
rgb
[FIXED. Thanks. -REP]
LazyTeenager says:
April 16, 2012 at 6:40 am
“Went looking
Rather than “models” we have the one model: ECHO-G. This is described here: http://www-pcmdi.llnl.gov/ipcc/model_documentation/ECHO-G.pdf
It is a 2001 vintage model and used as one input for AR4. In short quite old.
Don’t know how it compares to others leaving open the question of whether this model typically underestimates temperatures.”
So we agree that AR4 is outdated, and its projections were incorrect? Great! We’re making progress.
Maybe in 2025 we can come back together and assess whether AR5 was any better.
Lazy teenager said: “It is a 2001 vintage model and used as one input for AR4. In short quite old.”
So the old models were total bollocks. But they are good now. eh?
LazyTeenager says:
April 16, 2012 at 6:34 am
Older models have more semi empirical relationships built, in while newer models use more an initio calculations. This means that the newer models behave better over a wider range of physical conditions.
Children are supposed to behave — computer models are supposed to produce accurate results.
If two models disagree significantly, they must both be correct. Perhaps this is the proper way to model a chaotic system.
/sarc off
What happened to Popper’s view that proper science required falsifiability? If all the components of a model are accepted as proven science and the model does not track with historic data or provide reasonably accurate predictions as future data becomes available, either the model lacks some necessary components or the components have been improperly assembled in constructing the model.
“There’s a lot that indicates that some important factors have been completely under-estimated (e.g. sun) and other climate factors have been grossly over-estimated (e.g. CO2). Indeed the word “solar” is not mentioned once in the entire paper.”
In this study we have done a sensitivity analysis of the Holocene SST trends to changes in insolation associated with orbital parameters. In the models we used, only orbital parameters were modified, as it has been the first-order cimate forcing over the time interval studied. BY DESIGN, the sun activity or the CO2 cannot have been under or over-estimated as they were prescribed constant in the model.
It is very clear that “Dr. Sebastian Lüning, Prof. Fritz Vahrenholt and Pierre Gosselin” did not even catch the fundamental basis of what has been done in the article. This blog and its audience are probably the very last outpost where “Dr. Sebastian Lüning, Prof. Fritz Vahrenholt and Pierre Gosselin” can write such crap without feeling any shame. Thanks for them, idiots!