Statistical failure of A Population-Based Case–Control Study of Extreme Summer Temperature and Birth
Guest Post by Willis Eschenbach
The story of how global warming causes congenital cataracts in newborns babies has been getting wide media attention. So I thought I’d take a look at the study itself. It’s called A Population-Based Case–Control Study of Extreme Summer Temperature and Birth Defects, and it is available from the usually-scientific National Institutes of Health here.
 Figure 1. Dice with various numbers of sides. SOURCE
Figure 1. Dice with various numbers of sides. SOURCE
I have to confess, I laughed out loud when I read the study. Here’s what I found so funny.
When doing statistics, one thing you have to be careful about is whether your result happened by pure random chance. Maybe you just got lucky. Or maybe that result you got happens by chance a lot.
Statisticians use the “p-value” to estimate how likely it is that the result occurred by random chance. A small p-value means it is unlikely that it occurred by chance. The p-value is the odds (as a percentage) that your result occurred by random chance. So a p-value less than say 0.05 means that there is less than 5% odds of that occurring by random chance.
This 5% level is commonly taken to be a level indicating what is called “statistical significance”. If the p-value is below 0.05, the result is deemed to be statistically significant. However, there’s nothing magical about 5%, some scientific fields more commonly use a stricter criteria of 1% for statistical significance. But in this study, the significance level was chosen as a p-value less than 0.05.
Another way of stating this same thing is that a p-value of 0.05 means that one time in twenty (1.0 / 0.05), the result you are looking for will occur by random chance. Once in twenty you’ll get what is called a “false positive”—the bell rings, but it is not actually significant, it occurred randomly.
Here’s the problem. If I have a one in twenty chance of a false positive when looking at one single association (say heat with cataracts), what are my odds of finding a false positive if I look at say five associations (heat with spina bifida, heat with hypoplasia, heat with cataracts, etc.)? Because obviously, the more cases I look at, the greater my chances are of hitting a false positive.
To calculate that, the formula that gives the odds of finding at least one false positive is
FP = 1 – (1 – p)N
where FP is the odds of finding a false positive, p is the p-value (in this case 0.05), and N is the number of trials. For my example of five trials, that gives us
FP = 1 – (1 – 0.05)5 = 0.22
So about one time in five (22%) you’ll find a false positive using a p-value of 0.05 and five trials.
How does this apply to the cataract study?
Well, to find the one correlation that was significant at the 0.05 level, they compared temperature to no less than 28 different variables. As they describe it (emphasis mine):
Outcome assessment. Using International Classification of Diseases, 9th Revision, Clinical Modification (ICD-9-CM; Centers for Disease Control and Prevention 2011a) diagnoses codes from the CMR records, birth defect cases were classified into the 45 birth defects categories that meet the reporting standards of the National Birth Defects Prevention Network (NBDPN 2010). Of these, we selected the 28 groups of major birth defects within the six body systems with prior animal or human studies suggesting an association with heat: central nervous system (e.g., neural-tube defects, microcephaly), eye (e.g., microphthalmia, congenital cataracts), cardiovascular, craniofacial, renal, and musculoskeletal defects (e.g., abdominal wall defects, limb defects).
So they are looking at the relationship between temperature and no less than 28 independent variables.
Using the formula above, if we look at the case of N = 28 different variables, we will get a false positive about three times out of four (76%).
So it is absolutely unsurprising, and totally lacking in statistical significance, that in a comparison with 28 variables, someone would find that temperature is correlated with one of them at a p-value of 0.05. In fact, it is more likely than not that they would find one with a p-value equal to 0.05.
They thought they found something rare, something to beat skeptics over the head with, but it happens three times out of four. That’s what I found so funny.
Next, a simple reality check. The authors say:
Among 6,422 cases and 59,328 controls that shared at least 1 week of the critical period in summer, a 5-degree [F] increase in mean daily minimum UAT was significantly associated with congenital cataracts (aOR = 1.51; 95% CI: 1.14, 1.99).
A 5°F (2.75°C) increase in summer temperature is significantly associated with congenital cataracts? Really? Now, think about that for a minute.
This study was done in New York. There’s about a 20°F difference in summer temperature between New York and Phoenix. That’s four times the 5°F they claim causes cataracts in the study group. So by their claim that if you heat up your kids will be born blind, we should be seeing lots of congenital cataracts, not only in Phoenix, but in Florida and in Cairo and in tropical areas, deserts, and hot zones all around the world … not happening, as far as I can tell.
Like I said, reality check. Sadly, this is another case where the Venn diagram of the intersection of the climate science fraternity and the statistical fraternity gives us the empty set …
w.
UPDATE: Statistician William Briggs weighs in on this train wreck of a paper.
Scientists find a way to distinguish the aerosol particle signal from the weather noise
“(Phys.org)—Scientists developed a modeling shortcut to dial in a clearer atmospheric particle signal. A research team from the Scripps Institute of Oceanography, the University of Washington, and Pacific Northwest National Laboratory fine-tuned the winds simulated in a global climate model to better represent the winds measured in the atmosphere. Their technique increased the signal’s clarity by greatly reducing the signal noise. Their work produced shorter, more efficient simulations of the global aerosol particle effects on clouds and a better reception of the atmospheric particle signal.”
http://phys.org/news/2012-12-scientists-distinguish-aerosol-particle-weather.html
No wonder the peer reviewers want to be anonymous.
Just Amazing…
Another case of “Climate Science” done by folks who took one Stats class, then forgot most of it.
I grew up in an area where summer temps typically were over 95 F to 100 F in all of July and August. Sometimes we’d say (accurately) “It’s 110 in the shade, and there aint no shade”.
We did not have air conditioning when I was a kid, nor did much of anyone else.
That said: I’ve never heard of “congenital cataracts”. Heard of a whole lot of other diseases in the area. Polio (a sisters friend walked with a gimpy gate from it). Even Malaria ( only one case every few years). Oh, and plague is endemic in the rodents. But no cataracts in kids. Sorry…
By their reasoning, most of Africa is blind…
(Oh, that place where I grew up? Northern California… Yeah, we have plague, malaria, and more… come on down! Lucky for us, not many cases. Lots of DDT used for a long time at the right times. We used to play in the fog of pesticide behind the “mosquito trucks”… )
“Keep doing that and you’ll go blind”
That’s what our priest warned us about.
•••
Maybe with a big enough grant, a computer model could determine the number of cataracts caused by the 0.7ºC global warming over the past century and a half. The number might be alarming!
More public funding required.
Try applying this ridiculous statistical hogwash to short-term stock market transactions, and watch your portfolio evaporate to zero in about five trading-days.
Well, when you put it that way, it seems pretty obvious. Marvelous thinking BTW, but I can’t help wondering how something so obvious gets past so many people to allow this to be anywhere near to being written or published and especially when those people are are supposed experts, in positions of authority or at least educated. No wonder I am leery of the pronouncemenst of ‘experts’ in any field.
And the saddest part – paid for by two grants from the CDC. In other words we are borrowing our grandkids dollars for this tripe.
The 2nd saddest part is the disclaimer “The authors declare they have no actual or potential competing financial interests.” Other than coming up with anything creative to get grants the wave a danger flag of agw to keep those paychecks coming.
We didn’t have AC either. Maybe that’s why I need glasses?
I did have tubercular meningitis as an infant. Maybe it was raining that day?
More research funds are needed.
Roger Knights says:
December 19, 2012 at 8:49 pm
No wonder the peer reviewers want to be anonymous.
=====================================
Isn’t anonymous a HACKING organization ??
Hey, PEER REVIEWED science! And you have the audacity to even question it ??? lol
That’s not far from climate “science” is it? They must be speaking of anomaly temperatures. Wait, are these scientists climate trained?
One sees a lot of this in medical studies. “Power lines cause cancer!”
I note there was also a 76% chance of a “statistically significant” _reduction_ in birth defects in at least one category. Naturally they reported that too, right?
http://xkcd.com/882/
That means everyone in Queensland is legally blind…..
We want money…
I think they call it “data dredging.” Funny thing is that just earlier this evening I had almost the SAME argument used against me on some board: a claim that some study showed that childhood secondhand smoke exposure gave them cataracts as adults. Basically, if you perform enough studies looking at enough variables for enough conditions enough times… you can almost always count on finding at least SOMEthing out there to blame your favorite bete noir on.
– MJM
I heard of study for women who were planning to become pregnat, warning them from taking long, hot, soaking baths, as there was a high correlation between doing that and various birth defects. Now I’m wondering how many urban myths are out there, having been created by defective studies.
Down here, getting “blind” has a different reason, and that reason is far more connected to CO2 than the climate reason !! hic !!!
D Böehm says:
“That’s what our priest warned us about.”
The blind priest ??
Lark says:
One sees a lot of this in medical studies. “Power lines cause cancer!”
Thank goodness they are not very edible or smokable, then !!
Sadly, a lot more research grants are going to determine “the effects of climate change” rather than to studying if climate change is anything but normal. Cut off the money supply and you cut off the BS.
This is why we Australians enjoy a good party … blinded by the heat !
But, “congenital cataracts” ? More likely the ‘researchers have contracted so other “congenital” disease and are struggling with the embarrassment of it. Don’t worry boys and girls, there is a cure !
Regarding the ‘power lines cause cancer’ scare, I recall reading a paper many years ago that pointed out that the power lines [in Sweden, IIRC] were along highways. Higher rates of cancer were attributed to the power lines. But later investigation determined that the exhaust emissions from thousands of cars and trucks every day was the cause of the local cancer spike.
Our bodies are as transparent to cell phone frequencies as a pane of glass [otherwise you would have trouble receiving a transmission if your body was between the phone and the tower]. Being transparent to RF frequencies means that RF energy is not felt by our bodies’ cells. The cell phone/cancer scare is as fake as the AGW scare.
“Cut off the money supply and you cut off the BS.”
Hey, not yet….. once I finish my current task, I was sort of hoping to get myself some of those funds.
I could have issues if they ask what my position is on climate, but I’m sure I can manipulate my way around theat, been watching and learning from the ‘climate scientists’ 😉
Just have to learn to lie and distort the thruth, is all, then I’ll fit right in. 🙂
Streetcred says..
“More likely the ‘researchers have contracted some other “congenital” disease…
once you get rid of all the con……………..
“That means everyone in Queensland is legally blind…..”
and in Darwin.. just “blind”
http://www.dailytelegraph.com.au/archive/national-old/northern-territory-drinks-most-alcohol-in-the-world/story-e6freuzr-1225735132584
HaroldW says:
December 19, 2012 at 9:23 pm
Dang, and he did it without calculations … nice.
w.
Congenital cataracts? It’s worse then we thought!
Sorry, couldn’t resist.
“We assigned meteorologic data based on maternal residence at birth . . .”
While, they . . .
“summarized universal apparent temperature (UAT; degrees Fahrenheit) across the critical period of embryogenesis . . .”
and
“ particularly for exposures during weeks 4–7”
This isn’t likely a big issue but folks do move — so residence at birth and residence at 4-7 weeks may not be the same.
Then there is the “maternal fever” thing. Is it possible that some women had a fever during weeks 4-7? Would they remember months later even if asked? Were they asked?
Again, maybe this isn’t too important but I didn’t see how they controlled for either of these things.
The use of multiple significance tests is a well known problem in statistics. The use of many variables is problematic if they are correlated. Else use the binomial distribution. Its expected value Np is already telling. With p = 0.05 and N = 28 we expect 1.4 false positives among independent trials. I once tried to explain that to a researcher who used 60 variables in 60 significance tests and found 3 ‘significant’ results. I did not succeed and the same BS is still around. Problem seems to be very difficult.
Forgive me Willis for not sharing in your amusement. Some people take these people seriously. Even worse, a lot of people take the people seriously that drool over the prospect of using something like this to advance the cause of climate alarmism.
Pnce again poor science gets ‘Eschenbached.’
I am sorry. I was born at night, when the temp was so much lower. Maybe that is why I am not quite blind, yet? If Anthony has to watch his time of observation, don’t these folks with all sorts of degrees and perhaps even cataracts?
Someone I know very well and has an important role interpreting published science in a medical area for public policy makers, tells me that 90% of the published papers in his field are worthless because of problems like this. He tells me, most of it comes from doctors, who think they are scientists.
I googled 2 of the authors and both are epidemiologists. A discipline one would expect to know something about statistics.
I always thought people were homeotherm.
And that an unborn baby would be growing in a steady 37C environment.
How could a baby in the womb notice any change in temperature outside?
And how would it affect him?
And going from outside -20C in winter to +20C in your own house would be bad too?
I won’t bother to read the daft paper then! More seriously, this is exactly the kind of crap science we have come to expect. What bothers me is that this passes muster and is published.
Also, in relation to say, something that is non-linear and semi-chaotic in nature, I dunno, let’s say, something like ‘climate’ – it would be relatively easy to pick a variable and any number of the vast number of climatic ‘events’ and ‘interdependent variables’ and probably make a case for one ‘important’ variable being the sole cause of said events……Oh wait, now I get it, that’s why CO2 is repsonsible for everything!
To correct for multiple comparisons, some people use the Bonferroni correction, which divides your desired significance level (e.g. 0.05) by the number of comparisons. So 0.05/28 = 0.0018, which becomes the new threshold for finding any single comparison significant.
First off they used regressive analysis which can show a false correlation with one variable and they had several. Second, they cannot prove causation as this was not a controlled study. Maybe I don’t have the background to understand these statistical methods? The Rahmstorf and Foster paper also used a method similar to this one to get their “temps match IPCC” graph and I recently read a study on second hand smoke that was touted in the media as proof of the dangers and it was actually a meta-analysis which really blew my mind. I just finished my first stats course and from just playing around with some regressive analysis and sampling I was able to see the inconsistencies with these methods. If you don’t like your results, take another sample, remove outliers and try again, change the scale of your scatter plot. Lots of room to introduce bias…
Warmer temperatures will increase the growing range of golden rice, which prevents blindness in children, but not in politicians.
When I was growing up I had access to AC, it was called a window in summer and a fire in winter. But this study is just rediculous. Of course this had no effect on internal body temperature.
Clearly they didn’t bother with Wikipedia; A congenital disorder, or congenital disease, is a condition existing at birth and often before birth, or that develops during the first month of life (neonatal disease), regardless of causation. Of these diseases, those characterized by structural deformities are termed “congenital anomalies” and involve defects in or damage to a developing fetus.
More tripe just in time for Christmas!
Great post, Willis. Readers may like to visit Prof John Brignall’s wonderful Numberwatch site, where he has done an excellent demonstration on the statistical analysis carried out to day, where large numbers of studies display a Relative Risk ratio of less than 2, when 20 years ago, & before the invoking of the Precautionary Principle, any paper with an RR ratio of less than 3, was cut into small rectangles, bundled together with a small hole pierced in the top left-hand corner, hung on a looped length of string, & placed in the smallest room in the laboratory!!!!! I find it sad that as “ALL CHEMICALS” cause cancer especially by PDREU/UESR standards, scientists pump poor old lab rats full of a substance in volumes beyond a realistic level to supposedly simulate prolonged exposure over time, & the rat develops a tumour, & little mention seems to be made of a likely toxic shock to the system the rat may have suffered from chemical overload in a very short time frame! The press release is usually done before peer review has taken place & the press/media have a field day with yet another “we’re all going to die if we don’t do as we’re told” scare story!
I remember getting taught about the Bonferroni correction (and other options) for this multiple testing problems in my first-year undergrad general stats course about 20 years ago. It’s a very well known problem. Surprised (well, not really) the researches and none of the reviewers picked it up.
I hate to be picky, but 2 points on statistical terminology. In statistical significance testing, the p-value isn’t the probability it happened by random chance, but the probability of observing such a extreme result if the null hypothesis is true. If the null hypothesis is ‘random chance’ then it’s the same thing, but if I’m comparing two groups, 1 null hypothesis might be there’s no difference between them, but an alternative null hypothesis is that there is a difference of a specified amount. For the same data, I’d get a different p-value depending on which null hypothesis I’d identified a-priori as the one to test.
Secondly, a p-value is a probability, not an odds. An odds is the ratio of the probaility of success to the probability of failure, ie p/(1-p). While people often use them interchangeably, in statistics they’re 2 different things. Admittedly there’s not much difference if you’re talking about a probability of 0.05, but if the probability is 0.75, the odds is 3 (ie 0.75/0.25).
Here endeth the lesson. 😉
.’The p-value is the odds (as a percentage) that your result occurred by random chance. So a p-value less than say 0.05 means that there is less than 5% odds of that occurring by random chance.’
That’s not right,is it? If the p-value were a percentage, it would be ‘5%’, not ‘0.05’. . It can be converted to a percentage, but it is expressed as a decimal fraction.
As usual, Mr. Eschenbach got things wrong.
There’s actually no problem with his article, all the math he presents is perfectly correct.
What’s wrong are his assumptions on methods used in the PubMed paper which he apparently didn’t read carefully enough.
First of all, while the paper is inspired by IPCC conclusions, it is not about ambient temperatures at all. It is about heat waves and it even gives detailed description about what is considered a heat wave. And that definition makes pretty good sense both in New York and in Phoenix.
Second, while Mr. Eschenbach is calculating how likely it is that such result may come out of totally random data, he might have also calculated it for the results they actually present. That means, what is the total statistical significance of one result out of 28 having p<0.05 at three separate criteria at once, one result having p<0.05 at two at once, and remaining 26 being not statistically significant in any of the three criteria. Because done correctly, that state coming out of random data is actually pretty unlikely.
That article does not deserve such kind of treatment from Mr. Eschenbach, it is an interesting study. It may not be relevant for global warming for all of the reasons which were discussed on these pages thousands of times already but it still may be relevant to what people may want to care about during pregnancy.
Kasuha says:
December 20, 2012 at 1:48 am
Gosh, Kasuha, that’s a charming way to enter a discussion. You do realize that it reduces your chances of having people care about your opinion, don’t you?
Oh, please. How is a “heat wave” different from “heat”? Are you saying that the heat is a problem only if it doesn’t last long? I don’t understand this objection at all.
For example, a 5° summer heat wave in New York might be 10° colder than an average summer day in Phoenix, and last for a much shorter time … how can a cooler shorter “heat wave” in NY cause congenital cataracts, but not longer lasting, hotter temperatures in Phoenix?
Since you haven’t had the courage to present your mathematics, I fear that I can’t respond to that.
The odds that I have given are for one or more occurrences of p equal to 0.05. So it includes the other “significant” result already.
In addition, you have fallen into another trap that I didn’t discuss in the head post. This is that they compared the various congenital problems to several different measures of temperature. The measures were the mean, minimum, and maximum temperatures.
What neither they nor you seem to have thought about, Kasuha, is that we would expect the mean, minimum, and maximum temperature to be highly correlated with each other. If something is wellcorrelated with one of them, it is likely to be correlated with the other two.
As a result, your claim that they are significant “at three criteria at once” is not meaningful. Because the three criteria are well correlated, that is no more significant than temperature being correlated with any one of them.
Finally, you list out the peculiarities of the dataset. You have one condition significantly correlated with three measures, one condition being significantly correlated with two measures, and 26 with no correlation. You say that the chances of “that state coming out of random data is actually pretty unlikely.” And you are right, the chances of any particular specified state are low.
But we’re not interested in just that state. We are interested in all possible states that have one or more results of p = 0.05. There are many, many more of them then just the particular one that occurred in this dataset.
So while you are correct that the odds of that particular state are small, the odds that we’ll have at least one result of p = 0.05 are quite large, as I calculated above
w.
I concur with Kasuha’s comment above. This is a hypothesis-generating study and the authors stress the need to confirm the possible association in further studies. The authors seem to be well aware of the issue raised by Willis Eschenbach since they discussed it themselves: “Last, because we performed multiple tests to examine the relationships between 28 birth defects groups and various heat exposure indicators in this hypothesis-generating study, statistically significant findings may have been attributable to chance. Under the null hypothesis, we would expect 4 of the 84 effect estimates displayed in Table 3 to be statistically significant at the p = 0.05 level. […] However, the associations with congenital cataracts are biologically plausible, particularly given stronger associations during the relevant developmental window of lens development, and associations were consistent across exposure metrics, making chance a less likely explanation for these findings.”
Willis
You are right. There is no Bonferroni correction. The authors seem to think that performing multiple logistic regression will take care of their ‘confounders’, an additional indication the authors think anything that turns up in their univariate analysis must automatically be meaningful.
Cataract incidence is, yet, associated with three different temperature indices in their data. It would be worth applying the correction and then checking if these association still stand.
Where is the check for association between cataracts and urban heat islands? One may even swallow that heat islands don’t affect gridded anomalies in well-constructed climate datasets, but heat islands definitely affect individual people living them! Heat islands are definitive confounders, accepting the authors’ own findings.
Did the authors correct for Rubella immunization status? I don’t see it.
The incidence of cataracts may well be affected by confounders the authors list (for e.g., alcohol consumption). But importantly, cataracts occur in association with other congenital birth defects, as part of syndromes, a good proportion of which may be undiagnosed and therefore unreported. The authors don’t appear to correct for these.
The authors perform sub-analysis looking for association between congenital defects, but, only among pre-term defects. A reasonable guess is that the authors do this, simply because they are able to. Pre-term deliveries with congenital defects have such data recorded. But cataracts can be congenital and be associated with other defects, and yet not be diagnosed at birth.
The study design is possibly not the best for answering questions of the kind the authors raise. Their controls are people who were exposed to the same temperatures and gave birth to babies with no defects. How are they controls?! You’ve excluded the very effect you are trying to study from the controls. A better design would have been to randomly select individuals who gave birth during non-heat wave periods, irrespective of occurrence of birth defects.
These people are no more scientists than some people in the banking sector are wealth creators; where wealth = something of value and not just a symbol.
[MOD–Oh, bloody hell. Up late, on a netbook that I’m not used to, when the screen went dim–instead of trying to fix te resulting mess, it’s easiest to just put up this version instead.]
Actually, this is nothing like as bad as it looks at first blush. They got some hits, then looked closer, recognized the potential problem chance correlation, and said that their result looked interesting but would need confirmation.
In correlation tests of heat against 28 birth defects, they found statistical significance at the 5% level for thre:, congenital cataracts, renal agenesis/hypoplasia, and also a reduced occurrence of anophthalmia/microphthalmia. I’d expect the latter to be rare, and so have pretty poor sample size. But for cataracts, figure 2 in the paper shows the association as statistically significant during weeks 4,6, and 7. They state weeks 4-7 to be the time that the developing lens is most susceptible (as shown, e.g., by data from mothers with Rubella during pregnancy**.) That’s a bit less random than just getting a hit for statistical significance somewhere within weeks 3-8. Not startling, just noteworthy. They ran correlations against a few different criteria for hot weather,i.e., max, min, and mean temperature and got hits for cataracts with all of these. Since these ought to be fairly well correlated, it’s hard to tell how much that means.
I’ve heard of researchers taking a group of variables, running 100 cross-correlations, getting five hits at the 5% level, and presenting those, with a straight face, as though that were meaningful. These authors were aware of, and addressed, the problem of getting statistical significance by chance:
And, they say explicitly that these preliminary results need confirmation, with their last sentence stating:
**From radiation studies with mice and rats, they can actually pick a day to irradiate the pregnant animal, and get different birth defects depending on which organs are most susceptible that day. Couldn’t find a good web ref, but it’s in here:
http://books.google.com/books/about/Primer_of_medical_radiobiology.html?id=XylrAAAAMAAJ
Oh, yeah. Kasuha, please note that I have treated the three temperature conditions (max, min, and mean) as one, because they are well correlated.
If we include each of them as a separate temperature condition, however, we no longer have 28 possibilities. We have three times that many, 84 possibilities … and with N = 84, we are very, very likely to get false positives.
w.
As is typical, Willis provides excellent analysis. Still, I fully expect to read this story in the Sunday papers. Snip, snip…cut and paste. Big headlines.
Newspapers are in a death spiral and desperately need headlines that “break through”. The mindless readers (50% don’t get past the first paragraph) scan and digest. The information agrees with all the other flawed reporting, therefore they are comfortable with the story line, i.e., it is symmetrical with their level one thinking.
Pierre-Normand says:
December 20, 2012 at 2:46 am
Thanks, Pierre. Yes, indeed they did comment on that … but unfortunately, they didn’t seem to understand what it meant. They still claimed that their results are significant.
But what their own calculation means is that their results are not statistically significant. I don’t care if the outcome is “biologically plausible”. Not significant is not significant, and it should not be written up.
At least on my planet, results that are not statistically significant are not worth of a paper. These results have been hyped around the planet by the media, which clearly thinks they are significant and is reporting them as settled fact.
Now, why in the world would the media think that the results are significant? Here is the claim from their abstract (my emphasis):
Perhaps you could comment on the ethics of writing up a paper to present results that the authors know for a fact are not statistically significant, Pierre, and despite that, claiming in the abstract that the results are significant.
Because in my world, that is agenda-driven deception, and it has no place in science.
All the best,
w.
Cataracts are a common problem in Nepal, but this is due to the high altitude, and therefore thin atmosphere, allowing in more uv. Perhaps they could find a link to climate change there. http://www.cureblindness.org/
Without a lot of statistics behind me I tend to agree with Willis Eschenbach.
This study seeks significance at a very weak level, the sort that would be attempted in a student physiology t test.Were the groups randomly selected to eliminate bias from nutrition, housing demography genetics and culture? Was there an out of contact control group? As another commentator pointed out cataracts don’t seem to be a feature in hot climates, so when does a heat wave become climate change?
What is outstanding about these results is the lack of any significant damage in any subject, under the perceived conditions of heat, in the vast majority of heat sensitive embryological defects, in a study so open to random effects.
Further, quoting animal studies, it should be remembered that congenital cataract formation is a feature of some lines of dogs, especially in the cocker spaniel and has a strong genetic component.
If such is the case in man, then this study must lead to funding to genetically test parents so that their affected children may be identified and treated early to prevent further disability.
This is the appropriate public health response.
Excellent summary of the p-value! It’s odd they used a p-value of 0.05 as health fields typically require testing to 0.01 to reduce the odds of false positives .
By thecway, is there anything bad that global warming won’t cause?
Whoever reviewed this paper made a terrible brainless job. It is usual standard in biomedical epidemiological research to apply Bonferroni correction for multiple comparisons. Thus , agreed, the methodology is a nonsense. I personally review papers for top ranked medical journal (e.g. NEJM and JAMA) and I can assure everybody that a paper like this has no chance to be published in those journals.
Most importantly, statistics means nothing if there is no reasonable pathophysiological hypothesis to explain the finding (which actually should be the reason to perform a study).
BUT there is even more fun in this paper. According to table 3 there appear to be a protective effect of temperatures for the onset of anophthalmia/microphthalmia (OR 0.70 CI 0.52-0.93). So, if you heat a pregnant woman you have more chance of cataract but less eye gross developmental problems. Since cataract is curable and anophthalmia is not……. voting is open.
Not sure why you need to explain this, Willis – what they’re doing is little more than an infinite number of monkeys, and even Bob Newhart knew about those:
Now we just need to wait for the gazornanplat……
Hi Willy,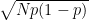 for
for 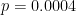 ) 5. Two sigma is 10. Sigma is commensurate with the expectation value — the worst possible case for drawing reliable conclusions.
) 5. Two sigma is 10. Sigma is commensurate with the expectation value — the worst possible case for drawing reliable conclusions.
Your argument is dead on the money. It’s simplest to just look at p itself — given 28 throws of a 20 sided die, one expects 1 (FP) to come up. Slightly more than one FP to come up, in fact. But this is not all.
In order to properly assess the impact of FPs, one has to use Bayes’ Theorem. The problem is that a broad population analysis of this sort requires one to know a lot about the prevalence of the diseases in question — both rate and details of distribution. So what, exactly, is the prevalence of congenital cataracts? Google to the rescue. In at least one study I just grabbed from the UK, prevalence was reported to be somewhere between 2.5 and 3.5 births per 10,000, depending on how long one waited to make the diagnosis. This distribution is not flat — as one article I found puts it: Congenital ocular anomalies are major contributors to childhood visual morbidity. Congenital cataract is one of the few of these visually handicapping disorders that is amenable to primary prevention—for example, through a rubella immunization program…
In other words, there are problems beyond applying a 0.05 “significance” test to a shotgun blast of studies. The disease has a fairly low prevalence and it has at least one significant confounding factor (whether or not rubella is prevalent in the community). Are there other confounding factors? From another study (all of them available unpaywalled online, thankfully): In southern India, the prevalence of congenital cataract is estimated to be 1 to 4 cases per 10,000 children examined.4 A major portion of these is hereditary, or genetic, in origin.
We see that the disorder is not only associated with whether or not the parents and community have been adequately immunized against diseases — something that for better or worse is unevenly distributed worldwide with temperate zone nations having a much higher degree of immunization coverage than tropical ones — but that the prevalence in southern India is almost exactly that observed in the UK. Now, I lived in northern India (New Delhi) for seven years in the 60s, right across that “Ice Age Cometh” dip in temperatures that had people worried going into the 70s, and it went down to freezing precisely three times in seven years. In southern India it didn’t get close — it is hot (even compared to northern India). New Delhi is easily 5F warmer than any point in the UK, on average — Bangalore is probably 10F warmer than the UK.
We also have the fact that, of the cases reported, at the very least many of them are hereditary — not caused by the heat but caused by inherited genetic factors that run in families. In fact the second article was looking at: The authors focus attention on congenital lamellar cataract, which is associated with the R168W mutation in γC-crystallin, and congenital zonular pulverulent cataract, which is associated with a 5-bp insertion in the γC-crystallin gene. — specific mutations. This is real science, of course, not shotgun-blast population studies.
I could continue to search, but I think it is already pretty clear that two things are true. First, prevalence is not particularly accurately known. In the UK, with first world medicine, they fail to diagnose 1/3 of the cases observed before the individual is 15 years old (hence the rise in prevalence with the age at first diagnosis). The prevalence there is slightly less than 4 in 10,000. In India the prevalence — which is likely to be reported less efficiently early on, but one presumes that even in India blindness is blindness and by age 15 a diagnosis is likely — is given as 1 to 4 in 10,000, which sounds like the final prevalence is almost exactly the same as it is in the UK!
Now let’s think about this: 6,422 cases and 59,328 controls. What exactly does this mean? In 60,000 iid samples, one would expect to get 24 cases of congenital cataracts. Sigma for this is (
To put it another way, suppose that only 15 people got congenital cataracts in this control group. Would that justify the conclusion that the prevalence in the general population is really around 2 in 10,000, not 4, just because it is only a 5% likely occurrence? Don’t make me laugh. Similarly, a prevalence as high as three sigma would be no particular cause for alarm, especially if the group were truly randomly selected so that the samples were reliably iid (it never is, but that’s another story).
Now consider the “case” group. 6000*0.0004 means that 2.4 individuals are expected to get cataracts in this group! Sigma is now almost 2. There is almost no rate at which this group could get cataracts that would be worthy of attention. Statistics just doesn’t work for small populations with a low prevalence.
This may not be the structure of the study — they could be trying something even sketchier than this — but one can, as you note, take great comfort in the large scale numbers between people who live all the time in hot South India versus the people who live all of the time in the cold UK. The prevalence in the two populations is more or less the same, with millions of individuals contributing to the prevalence numbers in both cases. End of story.
One is reminded of a famous study involving cancer rates of people living near high voltage transmission lines that was conducted in just this fashion, and got precisely this kind of result — examine a small population (compared to incidence rates of cancer) for all kinds of cancer. Some forms of cancer will (in the small population) always happen less frequently than expected, some about the expected rate, some more than expected. Look at 20 to fifty cancers, and at least one or two are going to be at rates unlikely at the 0.05 level. Publish, generate lots of alarm, and it takes years to get fear of living near a power line out of the collective minds of the people. Or what they are doing now with cell phones, ditto. Big, expensive, careful studies refute this kind of bullshit statistics but it takes years.
We should talk about p in random number generator testing sometime. dieharder, my test suite, generates a list of some 80 or 90 test pvalues. One cannot use anything as puerile as 0.05 rejection, because one expects four or five tests to fail at this level every run with a perfect random number generator! In fact, if this many tests did not fail, on average, one would be certain that the generator was not random!
Statistics is a two-edged sword!
rgb
Nah … that’s why there are biostatisticians.
This study indeed seems like a classic example of the “Data dredge”, well described by John Brignell: http://www.numberwatch.co.uk/data_dredge.htm
Yeah. Deserves further study. My bet is there is nothing there, but who knows.
Incidentally, one of the more interesting climate related illnesses is MS. It is far less prevalent in Queensland than it is in Tasmania.
A good explanation of data dredging. Anyone interested in this further might enjoy numberwatch.com
“Figures don’t lie, but liars can figure” attribution forgotten.
Another excellent piece, Willis. Keep up the good work. Will you ask the publisher for a retraction and to stop using the “experts” who reviewed this 3rd grade level paper?
Bill
“one-in-a-million chances crop up nine times out of ten” (Terry Pratchett, “Equal Rites”)
Also http://tvtropes.org/pmwiki/pmwiki.php/Main/MillionToOneChance (warning: seriously addictive site)
Psychologists, doctors, sociologists take the Stats 101 course and get away from the subject as quickly as decently possible. I remember (no link) a report in, I think, Discovery Magazine a few decades ago of a report on stress caused by air pollution and auto accidents on the California freeways. The study involved measurements of CO, particulates, etc taken along a major highway and they found that when these were high, there was a statistically significant correlation with highway accident deaths! I kid you not! Organizations like CDC, of course, employ statisticians in their studies because of the importance of keeping doctors away from the subject.
Why should we worry when global warming should be felt mostly in winter? Uhi on the other hand is something else.
John Ionnides (http://en.wikipedia.org/wiki/John_P._A._Ioannidis )has led the fight against this statistical nonsense in the field of medical research. Alas NIH does not seem to be listening or reading.
.
So if the paper is proven to be cr@p, and the paper was funded by the government – can we get our money back?
And if they resist such a proposal, can we sue? I would happily give $50 to a fund to sue the ass of these guys.
.
All this tells us is that the AGW ‘research’ bucket is still deep and well filled .
How much quality research has gone undone becasue the researchers have been unwilling or unable to link it to ‘the cause ‘ no matter how slightly and therefore been unable to get funding . Is a good question and one ,the answer to which, we may all come to regret.
Actually, what they missed in this report, is that congenital cataracts are caused by coffee. Our own assessment of this data has demonstrated that the mother of every effected child drank coffee during the pregnancy. Q.E.D.
Details of where to send the government grants, is available on application. Six figure sums only, please.
Willis,
I disagree that the result regarding cataract isn’t statistically significant. The hypothesis that was tested against the null hypothesis wasn’t that at least one (or even four) among the 28 possible associations would turn out to be significant to the 95% level. If that had been the hypothesis, then the fact that at least one such association would be significant wouldn’t itself be significant to the 95% level. This is something the authors clearly acknowledge. But rather, the study aims at testing several independent hypotheses. It could just as well have been 28 completely independent studies some of which would have produced significant results and some not. That among such a large number of studies, about 4 of them could have been expected to produce false positives isn’t disputed. It is in the very nature of results that are significant to the 95% level that 1 in 20 such result, on average, will be occur by chance — provided the null hypothesis is always true. But the individual studies that produce positive results still would have produces significant results. You can’t nullify the significance of the result of one single study simply by considering it in the context of a group of similar studies that test *independent* associations. That the researchers tested 28 independent hypotheses at once rather than publishing 28 different papers is irrelevant to the significance of the individual results since they are, indeed, independent.
I initially misread Willis’s reply to Pierre-Normand.
Willis is quite right that claiming significance in this case is deceptive. He was not claiming, as I originally wrongly thought, that we should not publish work that shows no statistical significance. To fail to do so is to commit the anti-science error known as the file drawer problem.
I fear that the file drawer problem is endemic in climate science. I cannot prove it, of course, since the evidence is not published; but I point out that the conditions of groupthink, ‘consensus’, activism and the widespread (fallacious) meme of being under siege by well funded hostile anti-science groups are precisely those conditions that would be most likely to exacerbate this problem.
Oh, and I’m sorry I didn’t get to refer to XKCD’s 882 first; as Willis notes, ‘he did it without calculations… nice.’
The “paper”is statistical junk. I have had a thing about medical research and the abuse of statistics going back to the ‘fifties. I devour these papers (which have become much less difficult to get hold of since the advent of the internet) simply because of the naivety of the statistical thinking which is a wonder to behold. This “paper” is not at all unusual in this respect – virtually all medical research papers are as bad or worse. The ones produced by good well meaning people I am talking about, not the ones produced by outright statistical rogues like the late Professor Doll (smoking) or the late Ancel Keys (dietary fats). It is my long held personal suspicion that those who are attracted to medical research are congenitally innumerate. They beat the AGW crowd into a cocked hat.
Sounds like vitamin D deficiency to me… Fixing it is no different than fixing Spina bifida with folic acid at the right dosage.,
http://www.thelancet.com/journals/lancet/article/PIIS0140-6736(96)91331-8/fulltext
Based on this study, pregnant mothers do much better at the daily dosage of 4,000 IU vs what is recommended 600IU which isn’t even enough to push us into optimal range of vitamin D level. No wonder why we get sick with cold or flu or infection easily during the cold months…
http://grassrootshealth.net/index.php/press/92-press-20100430
One could easily say that this disease happens more often in NY than AZ is because of long winter forcing us to stay in the house and not see sun much compared to AZ where winter is short and sun (specifically UVB sunlight) is more intense to help skin produce vitamin D… All you have to do is conduct vitamin D study. Very simple study.
Anyone even aware that during the midday with clean air in the summer in bathing suit without sunblock gives you 20,000 IU of vitamin D after 20-30 minutes (for Caucasian people)? The darker your skin gets, the longer it takes to reach 20,000 IU. It can be 10x longer for people with darkest skin color. The recommendation of 600 IU a day makes no sense. Someone made that recommendation on faulty science a long time ago. It used to be 200 IU a day 20,30 years ago. We paid the price…
While the statistics errors are bad – the lack of sensible checks against birth defect numbers in areas with high temperatures, or with the rate of birth defects in the cooler seasons are showing their medical ignorance. These would be extremely easy checks to make but of course the result would not get them the further research funding that they are actually fishing for. So the lack of sensible validation checks make the paper a waste of money. They might just as well state that having an air conditioning failure in summer causes congenital birth defects.
If they really want to motivate action, they should have released a study, whose results would indicate AGW causes a reduction in penis and breast sizes. With society’s fixation on this parameter, there would be an instant demand for a new LIA.
We really are a strange and predictable people. GK
Yes, that’s the fallacy behind clinical test batteries in check-ups. If you do 30 tests at least one comes abnormal and you can treat a patient for nothing but a false positive. When performing multiple tests the confidence level must be increased dramatically.
Jason T, it is good to see that they did a better analysis than appears “at first blush” as you put it, but they ignored the elephant while focusing on the mouse. There is nothing in science that is more dangerous than fishing for hypotheses in some vast pile of highly multivariate data. It is, in fact, a rather complicated logical fallacy.
The elephant involves — as Willis (and I) point out — simply looking at accurately known prevalence rates drawn from large populations that live all the time at temperatures that vary by 5F or more. Of course one doesn’t expect those prevalence rates to match perfectly even for large populations drawn from different parts of the world, because the population genetics is generally different, the background of confounding variables like immunization, exposure to teratogenic substances, radiation levels (which are a function of height above sea level, latitude, and specific environmental factors local to particular places) are all different. So even if they were different for these huge populations one’s utter inability to control for the confounding variables (most of which are simply unknown and unknowable) makes it impossible to resolve a temperature-based difference, although one can place an upper bound on it quite easily. A very, very small one.
To do better, one would require all the data in the world. Literally. Then one could coarse grain it (splitting the globe up with some appropriate tesselation of the sphere), visit all the tessera, measure or estimate all of the confounding factors and the mean temperature, and do god’s own fully multivariate statistical analysis. Ultimately, you’d need to show that temperature has unique explanatory power not confounded by mere accidental covariance with e.g. ultraviolet exposure in tropcial climates, pollution in industrializing third world countries like India (which is currently phenomenal) and so on.
As for the author’s argument that this is somehow “plausible”– humans are homeothermic animals. This means that it does not matter as a general rule what the temperature outside your body is — inside, it is 98.6F plus or minus half a degree F. When it is higher, we say that the individual has a fever. When it is lower, we say that the individual is hypothermic. Both are serious conditions, no doubt, but fevers occur routinely and no doubt occurred throughout the two populations throughout pregnancy at a more or less normal rate, which makes it rather probable that individuals in the populations had a fever for at least a few days while pregnant.
And here again, we have a very, very simple statistical test, one that the authors would surely have investigated if they actually gave a damn about being accurate rather than creating hysteria. For example:
http://www.healthline.com/health-blogs/fruit-womb/fever-pregnancy
What? Fever (hyperthermia) during pregnancy is associated with birth defects? Damn skippy it is! And what is the most common cause?
Over the years, several studies have confirmed that temperature elevations in pregnant women accompanying influenza and common cold virus infections are associated with greater risk for congenital anomalies, multiple and isolated, especially, neural tube defects.
Wait, wait, did he say neural tube defects? Not congenital cataracts? So that if the women in question actually had elevated body temperatures (hyperthermia) from having been in a warmer climate for one whole week of their pregnancy (snowbird trips to Disney World during pregnancy now being counterindicated) then it is almost certain that an increase in neural tube defects would have been detected before an increase in congenital cataracts?
Oh, and while we are at it, why not look in the literature at the connection between actual fever-induced hyperthermia and congenital cataracts? Let’s see:
http://eyewiki.aao.org/Congenital_and_Acquired_Cataracts_in_Children
The causes of infantile cataracts have been the source of much speculation and research. Making a distinction between unilateral and bilateral cataracts may be useful when considering etiology.
The majority of bilateral congenital or infantile cataracts not associated with a syndrome have no identifiable cause. Genetic mutation is likely the most common cause.
and
Systemic associations include metabolic disorders such as galactosemia, Wilson disease, hypocalcemia and diabetes. Cataracts may be a part of a number of syndromes, the most common being trisomy 21. Intrauterine infections including rubella, herpes simplex, toxoplasmosis, varicella and syphilis are another cause.
Then there is this one:
http://www.ncbi.nlm.nih.gov/pubmed/16323161
(from 2005). Conclusion: Some isolated congenital cataracts are preventable by rubella vaccination and probably by influenza vaccination in the epidemic period. In addition, our results suggest that using antifever therapy for fever-related respiratory diseases may restrict the teratogenic risk…
although also (and very interestingly):
A higher prevalence of influenza or common cold during pregnancy was found in the case group (55.9%) than in the population control group (18.5%; adjusted odds ratios [ORs], 5.8; 95% confidence interval (CI), 4.0-8.4) or in the malformed control group (21.7%; adjusted OR, 4.7; 95% CI, 3.2-6.9).
In other words, a fever during pregnancy almost certainly is a causal factor in congenital cataracts! And what are the most common causes for fever? The flu or the common cold, although rubella (in places where MMR vaccination is not routine) or any other illness likely to cause a high fever increases your risk by a factor of three (more if you adjust it to reflect the gaussian distributions).
OK, so this is probably enough. We can see that sustained hyperthermia during pregnancy can very probably cause congenital cataracts as a birth defect outside of its association with familial inheritance or e.g. trisomy of chromosome 21. So, is sustained hyperthermia associated with “heat waves” in the summertime? Do people get a “fever” when it is hot out?
And what about flu and the common cold? Are they more likely when it is hot outside?
People do indeed become hyperthermic during a heat wave — primarily the very old and very young. Hyperthermia is defined in this case as a body temperature over 100F (sustained) without having a fever, that is, without an external cause such as a virus. It isn’t normal — as I said, people are homeothermic and unless they are stressed or exposed in an unrelenting way to higher temperatures (such as working out in the sun, engaging in outdoor sports in the sun) without access to water or shade on a high-humidity day they tend to stay under 100F even when it is hot out. Extended exposure leads to “heat exhaustion” or “heat stroke”, with symptoms very similar to those of correspondingly high fevers.
However, pregnancy is not listed as a risk factor in getting heat exhaustion when it is hot out. It isn’t an implausible one — women are under stress, their surface to volume ratio changes, their baseline metabolic rate can be higher — but surely heat exhaustion would show up in the individual case histories of the people in the study, not just “exposure” to high temperatures. Where I live (North Carolina) it is always five degrees farenheit warmer than it is in upstate New York (where I also lived for a long time). But here we have air conditioning, or fans, or the sense not to sit outside in the sun on a hot and humid day when we are pregnant (if we can avoid it, and most can not to protect their baby but because being hot and sticky is uncomfortable).
Then there is the flu/cold factor. According to the CDC (see e.g. here:
http://www.cdc.gov/flu/weekly/index.htm#MS
one is hundreds of times more likely to get the flu in the winter months than the summer. The cold (also associated with the birth defect, recall) follows a very similar pattern — summer colds are rare, winter colds are commonplace. In fact, almost all the respiratory infectious diseases seem to peak in the wintertime. One’s chance of having a fever in association with these diseases is therefore many times higher in the winter than in the summer, which one would expect to partially or completely cancel any general hyperthermia-linked bump in the summertime.
In other words, even if the perfectly reasonable hypothesis that having an elevated core temperature for an extended time while pregnant is teratogenic and could result in a variety of birth defects, with neural tube defects leading the way, the risks of febrile infections peaks in the colder months and must at least partially counterbalance the risk of hyperthermia due to excessive summer heat. Indeed hyperthermia is a lot less likely to be sustained for periods longer than a few hours, while fevers can last for days, so one would expect it to be a smaller factor.
Of course, in both cases simple common sense measures can provide protection. Get a flu shot before you get pregnant, and avoid sick people while you are pregnant. If you get sick anyway, use an approved anti-febrile agent to reduce your fever until you get better. If you are pregnant, it isn’t a good time to play tennis on a sweltering day, and you need to drink plenty of fluids.
That takes us down to the final bit — linking this to climate change. First of all, there isn’t any evidence that the climate is “changing” at this particular moment. The weather every year is somewhat different, yes, there are heat waves and cold spells. If you look at the cdc data above, you’ll see that there were eight times as many pediatric deaths from flu in the cold winter of 2009-2010 than there were in last year’s mild winter, just as there were more deaths of heat stroke during last summer than there were in many a comparatively more mild summer in years before. Weather extremes of any sort cause distinct problems, and weather extremes happen somewhere all the time and everywhere some of the time. There is no evidence that these extremes are changing their distribution. There is no evidence that the climate is “currently” warming, where the meaning of the word currently with respect to climate is a rather sticky question (averaged over just what window).
But the bottom line is that the paper above produces a weak statistical link — one that inside the paper it is acknowledged to be too weak to form any sort of conclusion, because they saw the incidence of a different sort of birth defect go down in the same population at the 0.05 significance level, and it is as absurd to assert that the warmer weather was protective of one as it is causative of the other. But the paper title says otherwise, and it has already been grabbed and dumped onto environmental sites as “proof” of one more danger of CAGW. No doubt this will get added to the absurd epidemiological studies that claim to tell us how many additional people die every year “because of AGW” (count the begged questions) while they never seem to subtract the people that lived “because of AGW”, like the 250 extra children who didn’t die of the flu in 2011-2012 compared to 2009-2010, or the people who didn’t starve to death because of a premature frost in farm country.
Given the flaws, the paper should not have been accepted, not with its title. Basically what they showed is that there are no statistically significant correlations between “heat waves” and birth defects visible in a study of this size. This is strongly supported by a two-minute analysis of prevalence rates in different climates plus the fact that neural tube defects (the “coal mine canary” as it were) should have the greatest sensitivity to hyperthermia from all causes and was not observed to bump, something they failed to look at and that forms a powerful Bayesian prior that still further reduces the probable significance of their result. Their title claims otherwise.
Sadly, their title is understandable. Nobody wants to publish null results (even though, as Feynman pointed out, often they are the most valuable results to publish). Who will fund further work if you don’t get anything the first time around? And here, they get to tie their work to not one, but two demons — birth defects and the horrors of Global Climate Change. Funding for more detailed work is assured, and if that future work produces a null result, not a single soul in the lay population will ever hear a word about it — the urban legend is already established and this paper will never die.
rgb
Scarface says:
December 20, 2012 at 12:27 am
I always thought people were homeotherm.
And that an unborn baby would be growing in a steady 37C environment.
How could a baby in the womb notice any change in temperature outside?
And how would it affect him?
================================================================
It’s a sighting issue.
Doesn’t the temperature of a mother’s womb stay roughly the same even if there is a 5-degree [F] increase in summer????
Causes of congenital cataracts.
http://www.nlm.nih.gov/medlineplus/ency/article/001615.htm
The Harvard Nurse Health Study is another data dredge.
Nothing worthwhile ever comes out of that one either.
DaveE.
E.M.Smith says:
December 19, 2012 at 8:53 pm
Just Amazing…
Another case of “Climate Science” done by folks who took one Stats class, then forgot most of it….
>>>>>>>>>>>>>>>>>>>>>>
I doubt they even took a statistics course at all depending on the school. Probably some prof. spent a day going over how to use a stat. computer program and that was it. (Based on my undergrad required courses in chemistry and the one day intro to the field of statistics in an analytical chemistry class.)
For example a Biological Sciences major at Illinois State University (link) requires NO STATISTICS at the undergraduate level but does require a course in Ecology and Biological Diversity.
In the masters program you finally get one course **BSC 490/420.27 Biostatistics/Biostatistics Lab – 4 Credit Hours and an elective of BSC 450.37 Advanced Studies in Biostatistics – 3 Credit Hours
BSC 490/420.27 Biostatistics/Biostatistics Lab
This is a graduate course introducing students to applied statistics and data analysis using SAS. The goal is to prepare graduate students for using and understanding common statistical methods in Biological Sciences.
Actual course outline link
Depending on the teacher this could be just a course on how to plug numbers into a computer with little fundamental information on the correct use of statistics. The reading assignments do look reasonable however.
There is actually a wonderful opportunity here; of the 28 groups, one showed a predicted increase with increasing temperatures. But it’s likely one or more also showed a predicted decrease (!) of birth defects with increased temperature. A request for the raw data from the researchers will confirm this. If in fact it is the case, one would wonder why the BENEFITS of warming were not reported!
Of course Willis is correct and neither the predicted increase or decrease is likely real, but it would be great to hear the researchers explain away any selective omission of a predicted BENEFIT.
John West says:
December 19, 2012 at 11:40 pm
Forgive me Willis for not sharing in your amusement…..
>>>>>>>>>>>>>>>>>>>>
Occasionally we have to laugh to relieve the stress of realizing how very serious this whole subject is. It keeps sceptics from going postal. (High moral standards also do that)
Scarface says:
December 20, 2012 at 12:27 am
I always thought people were homeotherm…..
>>>>>>>>>>>>>>>>>>>>>>>>>
Yes we are and even in 100F (38C) I normally run 97.0F (36C)
In NC I run into 95F to 100F a lot since I spend a lot of time outside.
D Böehm says:
December 19, 2012 at 10:15 pm
Being transparent to RF frequencies means that RF energy is not felt by our bodies’ cells. The cell phone/cancer scare is as fake as the AGW scare.
=============
Water is not transparent to RF. It is the principle behind microwave cooking.
HAM (amateur radio) warns of the dangers of transmitting with an antenna held near to your head. This warning is given repeatedly in bold faced type, in all certification manuals and at all levels.
The problem with new technology is that we have not been genetically selected for adaption to it. Thus, by chance some individuals will be killed off by the technology until the gene pool consists mostly of those individuals that are resistant to any potentially harmful effects. A similar experiment with artificial fats introduced during WWII created an epidemic of heart disease in some western countries. Those countries that avoided the artificial fats, such as France, have low incidence of heart disease while eating a high cholesterol diet.
Yet to this day, while many scientists recognize the connection between fat and heart disease, they fail to recognize that only certain types of fats are a problem, and only to those individuals that are genetically susceptible. Those fats that have been eaten for many generations will not be a problem, because our ancestors would have long been killed off by them and we would not be here.
These fats may even have a protective effect, by blocking receptor sites in the body that would otherwise be occupied by artificial fats. Thus, by stressing a diet low in fat, scientists may in fact be giving the wrong advice and the wrong treatment. The Mediterranean diet shows that the cure to heart disease may well be to eat more fat rather than less, so long as the fat is the same as what your ancestors ate.
There are many parallels between this situation and climate science. Faulty scientific conclusions based on faulty use of statistics, with a cure that may be more harmful than the disease.
Alan the Brit says: @ December 20, 2012 at 1:28 am
….I find it sad that as “ALL CHEMICALS” cause cancer….
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Perhaps we can persuade ALL the Environmental Activists to take up residence in an chemical free environment for a week or so or even a CO2 free sealed environment for a day. (snicker)
Lewis P Buckingham says:
December 20, 2012 at 3:23 am
…Further, quoting animal studies, it should be remembered that congenital cataract formation is a feature of some lines of dogs, especially in the cocker spaniel and has a strong genetic component….
>>>>>>>>>>>>>>>>>>>>>>>>
Just to add, it is very strong in some lines of horses/ponies esp. the Appaloosa. Appaloosas are one of a few breeds that can have cataracts present at birth. and link 2
That the researchers tested 28 independent hypotheses at once rather than publishing 28 different papers is irrelevant to the significance of the individual results since they are, indeed, independent.
Sadly, this exhibits a profound lack of understanding of statistics. For one thing, the hypothesis were hardly independent, given similar mechanisms and an identical hypothesized cause. For another, the paper did present 28 results at once, but its focus was clearly on demonstrating a causal connection, not disproving one.
Look, one has a choice. One can publish a single paper that shows the distribution of p for all 28 tests because you assert that they are effectively independent trials, and perform a Kolmogorov-Smirnov test against the uniform distribution to see if the distribution of p is unexpected given 28 supposedly independent results or one can publish 28 independent papers, one per result, 26 of which are papers that announce a null result (each with its own value of p), one of which announces that summertime heating is associated with a protective effect against one kind of birth defect at the 0.05 level (yes, they in fact found that to be the case) and one of which announces a causative effect at the same level of significance. This did not happen. The paper did not present “the distribution of outcomes in a series of tests was totally normal and identical to what one would have likely gotten using simulation with fair dice and the null hypothesis” because that wouldn’t have been “exciting” and nobody would have read their paper. It was:
Population-based case-control study of extreme summer temperature and birth defects.
synopsized as:
Higher summer heat is associated with increased risk of a rare birth defect that can lead to blindness. A 5-degree increase in temperature was associated with a 51 percent increase in congenital cataracts. The strongest link in this new study was found during a specific time of pregnancy when the eye is developing. The finding could be worrisome given climate change and increases in extreme hot-weather events.
Where is the bit about its association with a reduction of a different sort of eye birth defect? Oh, only deep in the article.
All I can say is given 28 draws, it would have been very slightly remarkable if one of them had not had a 0.05 hit (and they got two, one on each end of things). Given 100 draws, it would have been very remarkable indeed.
Hypothesis testing is one of my primary games. One of the dumbest things about it is that 0.05 is a commonly accepted measure of significance. This is absurd — 1 in 20 chances happen all the time. This just means that, on average, at least 5% of what is published with this as the standard is crap.
The real proportion of crap (in the medical profession) is much higher because the whole medical research establishment is “infected” with rampant confirmation bias and cherrypicking — where failure to produce a KS-test on all the tests or portray the distribution of p at all is a form of cherrypicking — and further distorted by the strong ties between positive results of any sort and fame, fortune and funding at the independent research level, and profit at the corporate research level. If you’ve dropped a billion on developing a drug, you’d better find a population that will pay you two billion for it. If getting tenure or keeping your funding is dependent on your finding something “interesting” as opposed to a null result, well, you’ll find something interesting.
Pick a disease, any disease. Let’s pick something easy, such as getting the flu, which (as it happens) has a known cause. Nay, pick twenty eight such diseases. I don’t really care what they are. Now take a population — and again, I don’t really care what the population is, or how large it is, let’s say 66000 why not. Pick any distinguishable variable you like — whether or not one is left handed, or blue eyed. Do a simple correlation between the binary values of this variable and all twenty eight diseases, and you are likely to find that something — maybe staph aureous, maybe influenza, maybe HIV, maybe chicken pox — is correlated with being blue eyed at the 5% confidence level. That’s what makes this sort of shotgun approach crap!
In fact, take a fair twenty sided die and a common, ordinary unbiased coin. Roll the one a million times, flip the coin a million times. Form the correlation of one with the other. On average (repeating this entire experiment a million times) one of the correlations will be unlikely at the 5% level in every trial.
You cannot infer that the coin and the die are not independent by looking at only this one case, and that’s the first question of relevance here. It is, after all, difficult to assert that the coin and some side of the die are correlated when the data do not suffice to reject the null hypothesis that they are, in fact, independent. One necessarily implies the other.
So you tell me — does the evidence suffice to reject the null hypothesis of heat waves are independent of birth defects? Because if they are causative of a birth defect in particular, the data had better support this first, don’t you think?
But of course, nobody has heard of KS tests unless they actually know what they are doing, and sadly so very few people know what they are doing when it comes to hypothesis testing. Sometimes including actual statisticians — it is a difficult subject where Bayesian analysis and mad skills are often key.
The only good reason to believe that the heat is causative is because there is a secondary correlation with “the time that the eye is developing”, plus the fact that there is a known causative association with hyperthermic conditions produced by fevers. But there is no definitive proof that the individual women in question were, in fact, hyperthermic during their exposure, nor is there any sort of statistically significant difference between prevalence rates in radically different global communities with far greater temperature differences than studied.
Also be aware that we’re talking tiny numbers — expected prevalence in the control population is only 24 (really, a bit less!) and a “fifty one percent increase” is a dozen extra cases, which pushes it barely out to two sigma and a hair. A rule of thumb in statistics is that you need at least a population of 30 before one can really start to rely on the central limit theorem, and most people I know who do this sort of thing would cheerfully extend that to 100.
I’d rather rely on the prevalence rate in south India, where most women go through summertime pregnancy exposed to temperatures that are routinely 10F warmer than those studied in New York and where whole populations live without air conditioning, which is not 51% higher than the prevalence in New York (where there is lots of air conditioning in the summertime besides being a lot cooler), the US, the UK, or anywhere else in the temperate or arctic zone.
Really, don’t you think that more or less squashes the question entirely, at least until the data suggests that external environmental temperature causes birth defects at all, ideally in association with specific cases of noted/measured hyperthermia? The latter I’d believe, given the fever-birth defect linkage already in the literature, but somewhere in there one has to show that pregnant women are almost certain to get hyperthermia in hot summers to make the connection in this paper at all plausible. And this I doubt.
rgb
This is another example of poor meta-analysis from the department of spurious statistics. I spent 30 years in the pharma industry closely involved with clinical studies on drugs. An area were meta-analyses abound! As examples we have all heard of the supposed correlation (or not) between electromagnetic fields and cancer and HRT and cancer. Both the result of many confused meta-analyses with the golden grail of a P<= 0.05 generally not worth the trees they are written on. Good analyses require prospective studies which address the issues of confounding variables and which designed so that the outcome of the study is blinded to interested parties until the trial code is broken. Even in this case P<= 0.05 would be considered borderline and strong correlations would need at least a P<= 0.01. In open and uncontrolled meta analyses studies these spurious P factors are worthless unless they are used to indicate the direction of further real research. This principle also applies to most, if not all, meta-analyses used in climate science which as far as I can see rarely show high statistical correlations and since there is usually no attempt to control or analyze confounding variable are again not worth the multitude of trees, both as subjects of analysis and paper used to write them on. Unfortunately this also applies to both pro and anti global warming camps ( just in case this upsets anybody I'm strongly anti!). This is also the issue which divides Leif from the rest of the anti groups who regularly feature on this website. As I understand it Leif's view is that something highly significant is happening to the sun right now based on his observations however he believes he has yet to see any clear causal parameter which links changes in the sun with the climate on the earth. That's a rigorous position to take but I think it lacks any proposal for the linking mechanism i.e. a testable hypothesis. In the anti-Leif camp correlations abound without any testable hypothesis which might indicate causality with the exception perhaps of the Cloud Experiments which I assume are still on going.
Finally, in the areas of science were meta- analysis abound you find frequent, invalid, attempts to slice and dice the data to get a better fit (retrospectively) like infamous the tree ring studies ( not worth a tinker's cuss) and switching the basis of the analysis.- the hiding the decline method all of which have nothing at all to do with the science and all to do with protecting reputations, maintaining grant funding or political agendas (both non government – the green lobby and government – distraction from the real and difficult issues affecting the state) such is the poor state of climate research. Ho Hum!
The main problem is, looking at so many different things one must feel bound to find something. I see lots of life science studies that have marginal or questionable statistical effects. Statistical significance is by definition to in the life sciences it often is essentially meaningless, except to the dogma pushers.
There is actually a wonderful opportunity here; of the 28 groups, one showed a predicted increase with increasing temperatures. But it’s likely one or more also showed a predicted decrease (!) of birth defects with increased temperature. A request for the raw data from the researchers will confirm this. If in fact it is the case, one would wonder why the BENEFITS of warming were not reported! or so. That’s starting to be pretty unlikely, and the distribution of p in that case would almost certainly be visibly non-uniform.
or so. That’s starting to be pretty unlikely, and the distribution of p in that case would almost certainly be visibly non-uniform.
There was and they were. Sort of. The paper correctly — at some point — notes that the data don’t suffice to show either one. They call — naturally — for more work to be done because of this. But AFAIK they didn’t do a full KS test on the distribution of p from all 28 tests (which wouldn’t have been very reliable, but might have been revealing in its own right even as a population histogram). The most important question is whether or not this distribution is or is not more or less flat. If it is flat enough that the KS test yields a reasonable p-value, one cannot reject the null hypothesis of “heat waves do not cause birth defects” just because one birth defect in the distribution tested came out with any particular value of p.
Here is a really lovely thing I remind people who don’t understand hypothesis testing. It is just as likely to get a p-value in between 0.475 and 0.525 — which nobody would reject — as it is to get a p-value in between 0.00 and 0.05, for any test where the null hypothesis is statistical independence so that outcomes are randomly distributed. You would be precisely as well-justified in rejecting a random number generator, or any other process designed to produce a p-value (that is, if correctly done, a uniform deviate per test) because it gave you a number in the former range as in the latter.
Hence the strong need for KS testing of the distribution of p, or the insistence that a p value be really low to reject the null hypothesis, not 0.05. I don’t even like 0.01. 0.001 is OK, depending on how many samples you plan to draw, but I play with random number generators far more than is healthy for any fully grown man, and hey produce numbers smaller than 0.001 — one thousandth of the time. I like to reject null hypotheses when p from a good KS test applied to the p-values produced by many independent “runs” of some testing process gets down to
Or one can (sometimes) do one’s stats on the cumulated data and get to the same place, even more accurately. In this case one can easily do this by comparing population prevalence between tropical and temperature climate countries. If the paper we are discussing is correct, it predicts that there should be at least a 50% greater prevalence in the former than the latter, absolutely clearly resolved. Furthermore, one should be able to associate the outcome with specific cases of clinical hyperthermia, hyperthermia that somebody actually measures, and relate the surplus to increased risk due to e.g. fevers in a quantitative way.
It isn’t that the claim is falsified by the study. It is that it is absurd to claim that it is verified, and a meta-glance at the overall data suggests that it is unlikely and shouldn’t even be thrown out as anything but a null result without answering a lot of questions that this study does not answer.
rgb
David L says:
December 20, 2012 at 4:18 am
By thecway, is there anything bad that global warming won’t cause?
Well…it does seem to lower the IQ of so called “climate scientists” by about 2 orders,so…oh wait…that is bad.
HAM (amateur radio) warns of the dangers of transmitting with an antenna held near to your head. This warning is given repeatedly in bold faced type, in all certification manuals and at all levels.
I looked at this, in detail. The issue is one of skin depth at the frequency in question, power in the transmitter, the utter lack of resonant transitions (this is not ionizing radiation). A cell phone is about as dangerous as a flashlight held against your head. Less dangerous than a powerful flashlight. Or going out into the sun. The sun is way, way more dangerous — it actually does hit you with dangerous ionizing UV (which is indeed carcinogenic in measured ways) in addition to some 300 to 700 times as much broadband electromagnetic intensity as your cell phone. The skin depth at the frequency in question is around 1 cm, meaning that most of the less than 1 W total power doesn’t even make it inside your skull, and becomes a warming “noise” utterly indistinguishable from your baseline core thermoregulated temperature.
I’m a physicist — if you want me to believe in a cell-phone — cancer connection you’re going to have to show me how the radiation can degrade DNA. It ain’t doing it by heating it. Again, beware results at the edges of “statistically significant” by the paltry 0.05 standard, pulled out of shotgun population studies or advanced by people infected with confirmation bias and with a dog in the race. Beware even then of confounding factors — maybe cell phones leach heavy metals into the air while operating and it is these that are toxic, or people who own cell phones are likely to drink coffee decaffienated by rinsing with an organic solvent that remains residual in the coffee and causes cancer. Correlation isn’t causality, and causality has to be physically plausible if not verified. Show me cell phones degrading DNA at standard powers from 2\pi steradian solid angle radiation at a distance of 2 cm and through a layer of watery skin and bone.
rgb
REPLY: I agree. As a broadcaster, we don’t have such warnings mandated for people who work around TV/radio transmitters where ERP is in the tens to hundreds of kilowatts range. If there were issues at VHF/UHF frequencies and power we routinely deal with, surely the FCC would have mandated warning labels. Microwave frequencies typically will cook your eyes before your brain (a standard warning from my days working on S band and C band weather radars) with pulsed ERP’s in the megawatt range, so I tend to laugh at the worries over cell phone and WiFi router radiation int he milliwatts range. I’m also an amateur radio operator, and with the exception of a few worry worts in my circle, few care about the issue. Note that police and firemen carry the same sort of equipment daily, and if there was some provable cancer causality, you can bet the police and fire unions would be all over it for improved health care/risk benefits, but they aren’t – Anthony
TonyBerry says:
December 20, 2012 at 7:55 am
…a bunch of stuff I agree with so strongly that it makes me weep to read it. I swear, nobody understands either statistics or quantum mechanics (which is kind of like complex statistics, which might explain the latter difficult).
Nothing helps you see the light regarding hypothesis testing more than writing something like dieharder, which is an engine for doing nothing but hypothesis testing. Play with dieharder and a perfectly good random number generator and you’ll quickly come to appreciate Marsaglia’s poignant observation that “p happens”. Read some of my remarks in the documentation and you’ll see why one cannot produce “certified random numbers” by producing sequences that pass the whole battery of tests, because an ensemble of such numbers will always fail the tests, they cannot possibly be random (you’ve cut out the tails!). Read about why you expect a handful of tests to fail on any given run at the 0.01 level (there are hundreds of tests that generate p values in a run) — and then there are the broken tests.
Then we can talk about predictive modeling in strongly multivariate nonlinear milieu. Oh. My. God.
rgb
One final reply that says it all — in fact, pulled from the link on the wikipedia page on data dredging — that could have been 100% of Willis’ article above as one series of pictures is worth a few thousand words:
Obligatory XKCD — jellybeans cause acne. Pardon me, only green jelly beans cause acne.
http://imgs.xkcd.com/comics/significant.png
Gail Combs says:
December 20, 2012 at 7:18 am
John West says:
December 19, 2012 at 11:40 pm
Forgive me Willis for not sharing in your amusement…..
>>>>>>>>>>>>>>>>>>>>
Occasionally we have to laugh to relieve the stress of realizing how very serious this whole subject is. It keeps sceptics from going postal. (High moral standards also do that)
==================================================
A gag a day helps prevent gagging.
Given that Lucy was found in the Rift Valley I would think that any problem with heat or heat waves would have been bred out of us along time ago.
“However, our findings for congenital cataracts must be confirmed in other study populations.”
India: millions spent on cataract surgery, zero spent on sunglasses.
How did this pass PEER REVIEWED, shows how dogma works.
Alarmist’s do remember that many hot regions are much warmer than elsewhere, so this globe warmer than x in future is always a fail from the start. These hot regions are here now, so x,y,z in future is already shown now that it’s false. Will you ever learn, of course not while dogma exists and there is no science involved supporting these conclusions.
Gail Combs says:
“Occasionally we have to laugh to relieve the stress of realizing how very serious this whole subject is. It keeps sceptics from going postal. (High moral standards also do that)”
I reckon so. I guess this farce can’t go on forever and we’ll have the last laugh. Sorry to have been a wet blanket, perhaps I’m low on cholecalciferol, I’d better get outside for a bit.
Some excellent discussion above of p values and their meaning. 🙂 Heh, if I took a pair of dice and rolled snake eyes on my first roll, should I label the dice as biased? They’ve obviously produced a result with a rather small probability of occurring by chance after all!
One thing to guard against that I believe you have not yet been hit with: moving the acceptable p value for public policy decisions from .05 to .1 — doubling the chances of the result being due to chance. Don’t get too comfy though: the EPA did it for “passive smoking” in their 1992 Report that ushered in US smoking bans and they can just as easily do it for studies regarding climate change. All they have to do to legitimize it is ignore studies going in the contrary direction and declare that it is “agreed” that causal results (of something like CO2 and warming) can only go in one direction. That will then allow them to use a “one-tailed” analysis, doubling the p-value. The media tends to be uneducated in such things and will just take the word of “the authorities” as being correct: a 90% finding will then be hailed as “statistically significant proof” and the hole will be very difficult to dig your way out of.
rgbatduke: Very interesting info on solar radiation! I’ve used the “less dangerous than sunshine” analogy many times in my writings on smoking bans by comparing the need to “protect the workers” in outdoor dining patio situations: after all, as the true believers like to say, “Why should THEY be the only workers forced to risk their lives for a paycheck? (Outside venues) are neither inherent nor necessary for dining or drinking. Serviced patio dining needs to be banned!” But when I’ve made the argument it was based mainly on risks of skin cancer. I had no idea that there might be an even more bogus cell-phone-connected argument to make! LOL! Hey, does cell phone use contribute to global warming???
:>
MJM, Cell phone and sunshine exterminator! Reasonable rates. Termination with extreme prejudice incurs extra charges. Ask about our “80% statistical significance special” (available only on alternate Tuesdays.)
EMSmith says
We used to play in the fog of pesticide behind the “mosquito trucks”
==========================
Myself, back in the days of DDT. Can’t lay an egg.
rgbatduke says: “Jason T, it is good to see that they did a better analysis than appears “at first blush” as you put it, but they ignored the elephant while focusing on the mouse…”
Just want to say I always enjoy your comments.
Willis Eschenbach: “agenda-driven deception”
Again Willis has put his finger on the nub of the problem. As he points out, the whole issue is settled by comparisons with incidences in warmer climes, so easy to do.
Could it be that this did not occur to the researchers? I doubt it. What this study is actually about is the art of hooking grant money, and these researchers are applying their own brand of AGW panic to shake down some loot.
I wish I had the means to put some kind of trace on the authors, to see if they succeed.
Yes, just to make the point clearer, you’d have to pick the specified significant variable in advance of doing the study to get kashua’s result. Saying, “This variable will be significant” is a much tougher standard than “Some variable will (appear to) be significant.”
Heh, if I took a pair of dice and rolled snake eyes on my first roll, should I label the dice as biased?
Possibly. It depends on your Bayesian priors. Bayes theorem actually tells you HOW MUCH you should presume that they are biased given the data and any given initial prior. That is, if you start out with the prior assumption of an unbiased die, held with some numerically stated degree of confidence and then roll a 6, how much “should” that alter your best estimate of the probabilities for the die on the next roll? Bayes theorem will actually answer that, if you let it. If you get the book “Doing Bayesian Analysis” with its cute-puppy cover, you can even walk through how to answer this quantitatively using R.
See “Polya’s Urn”, or (as I first encountered it) how to use Bayes theorem to evaluate the most likely probability for a two sided coin given the data in the context of learning statistical mechanics. Answer: Maximize (information) entropy with your answer.
That’s the other great tragedy — aside from the fact that the article could be a poster child for scientists who need a twelve step program to stop data dredging (see xkcd comic above, a perfect fit right down to the headline) — Bayes alters everything. We don’t actually do statistics any more by just counting — we know too much for that to make any sense. Bayesian priors — especially prevalence — are critical to any assessment of false positive/false negative rates in epidemiology, in addition to helping you understand the Let’s Make a Deal paradox, why when you are shown three doors (one of which holds a treasure) and you choose one, then somebody opens one of the two unchosen ones to show that it is blank, you should change to the other (remaining) door to maximize your chances of winning. Assuming, of course, that the person isn’t trying to game you by assuming that you will do this, and is required to always offer you the choice.
Statistics without Bayes is like, well, often just plain wrong, especially in the arena of hypothesis testing.
rgb
Well, I came back here this AM to add some sanity to the thread, and I find that rgbatduke, Dr. Robert Brown of Duke University, and TonyBerry have already done it amazingly well, far beyond my poor powers to add anything.
Many thanks, Robert and TonyBerry, for adding depth and substance to my initial efforts,
w.
I second Willis’s thanks.
I have just enough statistics training (a couple of semesters) to know when to scream for help. Too bad most scientists who write these papers are either too arrogant or ignorant to do the same.
I’ve learned so much from your guest posts here!
I’m wondering about blindness in New York city. The other day, I was watching a cable channel that was giving the projected high temps for the New York City area. I don’t remember what they were, but the projected “HI” for the city was 10 degrees F higher than the suburbs – I guess this means that kids in the city are all going blind and God only knows what all else.
Seriously, if they’re going to do studies like this, it seems a lot smarter to test people living in and out of the urban island effect in the same region.
Rg, I’ve always had trouble with that Deal paradox. Say I had a thousand doors and 999 of them had nothing behind them and one had a zillion samolians. I pick one and clearly have one chance in a thousand of winning. Monty Hall then randomly opens up 998 of them and they all display nothing. The chances at that point of the door on my left (which I had picked originally) having the zillion should be, as far as I can intuitively be comfortable with, 50%, i.e. the same as for the other door. And yet the Monty Hall “explanation” *seems* to tell me I should switch my choices to the door on my right.
Somehow that has NEVER sat comfortably in my gut. It simply feels like a joke being played by statisticians to see how gullible people can be.
– MJM
Statistics is bloody difficult. He says sitting here with three books on R and Bayesian analysis and two books on javascript at hand, with a dozen more in the house and work, trying to learn R and javascript both so I can learn to use mongo (huge database program with a huge database that speaks JSOL) and R in order to do predictive models both within R and with a proprietary neural network I wrote, once I integrate the db contents with all three. Yesterday. I know a lot, and I understand its basis (which is worth more), but there are huge chunks of stats I still don’t know, or learn only as I need them. I’m at the bleeding edge as far as Markov processes are concerned and multivariate predictive modeling is concerned, way less expert in boring old regression, pretty far out there in Bayesian analysis, and yet there are plenty of tricks used in mundane stats I’ve never used and don’t know. And I can do calculus and algebra and all that (as well as code, obviously, in too-many-languages-to-count+2 new ones, truly expert in C).
Pity the poor suckers like Michael Mann who actually wrote a PCA package in fortran so he could do his tree-ring work. Along comes M&M who actually use, um, R (because other people wrote it, and those people are really, really good at statistics and keep rewriting it and improving it and adding onto it as bugs are discovered, and besides, it’s bone simple to use once you’ve learned its data structures as it does nearly anything you want, the way you should be wanting to do it, automatically and by default once you get the data loaded in at all) and show that his results are bullshit with a few well chosen simulations and exercises.
Back when I was a grad student and early postdoc, I used to write my own numerical code (and yeah, usually in Fortran, as that was sort of the default physics language in those days). Fortran on IBM mainframes, fortran on PDP 1s and 11s, fortran on a Harris 800 (with the Vulcan operating system no less and 3 byte word boundaries), fortran back on a mainframe, fortran on an original 64K motherboard IBM PC, fortran on several AT clones before I converted to C in 1986 and never looked back. My excuse back then is simple — numerical libraries cost a fortune and nobody had them. Nowadays, I use the Gnu Scientific Library and try NOT to write my own code for standard stuff like statistics (although I’ve written a ton of stats routines in the past) because all it takes is one boneheaded bit of code and you’re screwed — garbage in OR garbage code equals garbage out.
Pity also physicians who are trying to do research that involves a serious statistical analysis. One stats course does not an expert make, and that is precisely what most of them have. If that — a lot of them took calculus in University, not EVEN one course in stats. As a consequence, they probably have never even heard of “data dredging”.
If they had, they would never claim that green jellybeans cause acne in a snipe hunt involving 28 possible hypotheses against one binary variable. In fact, they wouldn’t publish the results of the snipe hunt at all — they might legitimately use it to formulate a hypothesis to be tested against completely new data after looking carefully at some of the issues listed above, e.g. the lack of meaningful or corresponding differentiation of total prevalence (already well known) with climate, which suggests that if the effect they observe is not cosmic debris, a purely random occurrence as it is more than likely that it is straight up, it is confounded by other factors that are much stronger.
The hypothesis itself is perfectly reasonable. But you can’t discover the association and test it with the same data set, certainly not in a snipe hunt among 28 snipes with p set at 0.05. certainly not when the differentiation is small changes in a well-known probability.
I mean, which is it? Did the heat wave make the probability 0.0006 (a 50% increase) compared to the control population and was the control population still at 0.0003-whatever (since AFAIK it is only known to be “between 0.0003 and 0.0004” in the US in general)? The smaller subgroups they are trying to analyze have an even smaller representative population. Not only were the jellybeans green, but they worked the best on people believed to have acne that is sensitive to sugar.
I wonder why the blue ones don’t?
rgb
Presumably, under proper process, the subject/studies under analysis should have answered a questionaire designed to eliminate extraneous and/or conflicting variables. Did that questionaire include appropriate questions and sufficient information to determine if the other threatened cause of blindness was not being consummated?
Sorry. I am 67 and don’t have the time to go through 110 comments so if anyone has already made this point, ignore me!
I believe the correct way to procede would be to say:
“There is no real evidence for a link between 27 out of the 28 conditions hence we can ignore those and look at the only 1 which has triggered what might be a significant link. Two questions come up. Is there a causal link between temperature and the condition we are studying? Common sense suggests there isn’t (based on the Phoenix/NY arguement). However, if you are really sure this is a critically important problem, do the test again using other data from another place. Surely there are plenty of big cities which have an increase in temperature (UHI effect) and equally surely there are other sets of health studies. If you find that of the 20 sets only 1 does NOT show a significant correlation then you have some kind of evidence that there is a genuine (i.e. P=0.05) correlation.”
THEN you have something to publish and get your fame and glory. But only, of course, if you can find a causal link between temperature and your condition.
For example,there is a strong correlation between the temperature in London and the percentage of men in Germany wearing coats. Does this mean that wearing overcoats in Germany is caused by the temperature in the London streets? Or could it just be that the common causative factor is winter in the Northern hemisphere?
Down under, the outback aboriginals do have an increased level of eye problems, and they do live in very warm places. But the two are not causally linked.
As soon as decent medical care is available from a young age, the problem lessens considerably.
The problems does not exist anywhere near as much for urban aboriginies.
So yes, Alan, coincidence does not imply correlation, and correlation does not imply causation.
Meanwhile, back at the UN ranch.
This would have been the second surprise. Throughout the epidemic, science has been the last thing the UN’s political leaders have wanted to talk about.
http://www.winnipegfreepress.com/opinion/westview/UN-fakes-effort-to-help-Haiti-184151891.html
Blind? Please… just until I need glasses…
From the Readings section of Harper’s magazine, January 2013 issue.
The following comes from the instruction manual of a board game called “The Settlers of Catan” Developed by the Worldwatch Institute and the game’s manufacturers.
During your turn, you can convert one oil into two non-oil resources of your choosing. Alternatively, you may choose to forgo the usage of oil, sacrificing some growth for increased environmental security and the prestige of being a sustainability leader. The first player to have sequestered three oils gains the “Champion of the Environment” token.
For every five oils used, an environmental disaster results. Roll the two six-sided dice to determine where disaster strikes. If a seven is rolled, a natural disaster triggered by climate change floods the coasts. Settlements bordering a sea are removed from the board, and cities are reduced to settlements. Roads are not affected. A metropolis (because of its seawalls and other advanced design) is also not affected. If any other number is rolled, industrial pollution has struck. If the affected hex does not contain an oil spring, remove the production-number token from the hex. That hex no longer produces resources.
If the fifth number token is removed from one of the hexes, flooding has overwhelmed Catan and all inhabitants are forced to abandon the island, thus ending the game. While no player truly wins, the player who currently holds the Champion of the Environment token is recognized by the international community for his/her efforts to mitigate climate change and is granted the most attractive land on a neighboring island to resettle.
michaeljmcfadden says:
December 20, 2012 at 1:11 pm
“Rg, I’ve always had trouble with that Deal paradox. Say I had a thousand doors and 999 of them had nothing behind them and one had a zillion samolians. I pick one and clearly have one chance in a thousand of winning. Monty Hall then randomly opens up 998 of them and they all display nothing.”
Monty’s not opening the doors randomly. He’s opening them because he knows they don’t contain the zillion samolians. Each empty door he opens gives you a little more information than you had when you made your original choice. If he were opening them randomly, your gut would be right.
@michaeljmcfadden
“Rg, I’ve always had trouble with that Deal paradox. Say I had a thousand doors and 999 of them had nothing behind them and one had a zillion samolians. I pick one and clearly have one chance in a thousand of winning. Monty Hall then randomly opens up 998 of them and they all display nothing. The chances at that point of the door on my left (which I had picked originally) having the zillion should be, as far as I can intuitively be comfortable with, 50%, i.e. the same as for the other door. And yet the Monty Hall “explanation” *seems* to tell me I should switch my choices to the door on my right.
Somehow that has NEVER sat comfortably in my gut. It simply feels like a joke being played by statisticians to see how gullible people can be.”
You are incorrect and the Monty Hall expanation is correct. This has been tested by Mythbusters.
Look at it this way. For any N door contest with only one prize the probability that the door you select does not contain the prize is N-1/N.
When the host is opening empty doors he knows which door has the prize and won’t open that door. Because of this it doesn’t matter how many doors are opened, the odds you selected the wrong door don’t change and all the extra probability goes to the remaining unselected door.
You will always have better odds switching, the greater N is the greater the advantage to switching.
But ONLY
(1) if the host knows which door has the prize as he opens the remaining 998 doors
AND
(2) if the host decides to act on that knowledge.
If either of the above is true, then your odds have not changed.
Long story short —
Put nicely that is.
RA, Matt, TT … Thank you! Your comments, along with my own posing of the puzzle in extreme form, have enabled me to finally break through on both an intellectual AND a gut level. Given the host’s deliberate avoidance of the prize, it would appear to be a near-certainty (Well, 998 out of 999?) that the other door holds the prize. Clearly, the chance for the one that I picked originally was only 1 in a thousand. I’m still a *little* fuzzy on the fine points — as I’ve freely admitted at other times in statistical discussions on the net, although I had graduate level statistics, it was never my strongest suit. (Heh, plus it was a while ago.) — but at least now I feel comfortable in looking at the problem and telling myself, “Yup. It’s real. Switch yer choice!”
:>
MJM
willis and rgbatduke make for a helluva one-two punch.
Small biotechnology companies with new drug candidates use a slightly different trick when they can’t demonstrate with 95% confidence that their candidate drug is beneficial. They will look inside the group of patients in their clinical trial for a sub-population of patients that did show an unambiguous effect (p<0.05). Perhaps men responded better than women, or healthier patients better than sicker one, or those who hadn't tried anti-cancer drug A responded better to their new drug than those that hadn't. If you look at 20 or so sub-populations, the chances of finding one that clearly benefited (p<0.05) go up a lot. So the company goes to the FDA and requests approval to sell their new drug with information indicating that it should only be given to the sub-population that responded. (Doctors are allowed to prescribe an approved drug to anyone they think will benefit, no matter what the label says.) The FDA, which employs many statisticians and understands these tricks says, run another large expensive clinical trial consisting only of patients you expect to benefit and demonstrate that your drug is beneficial with p<0.05. The company then run to the WSJ and gets them to write an editorial about how the FDA's arbitrary on capricious rules are going to bankrupt another small company with a drug of proven efficacy in a particular group of patients.
I don’t remember if it was the WSJ at the moment, but your story reminds me of a study where the researchers got headlined as showing that exposure to a certain substance caused “hypertension” in “boys as young as eight years old.” The “hypertension” was an increase of roughly 1 unit systolic, and the pool of boys was actually a range of 8 to 17 years old, but the headlines didn’t go into that sort of detail of course.
The stories weren’t much better, although one of them *did* mention that the deadly exposure happened to DEcrease systolic readings by almost TWO points among girls. The researcher was asked about that and noted that decreased blood pressures could also be a health threat.
No, I’m not kidding. I can dig out the refs if anyone wants.
– MJM
I thought that biological plausibility of the of the results for congenital cataracts lent some support to the idea that there could be a causal relationship, but I’m backing off of that. It’s true that all of the statistically significant connections between heat and cataracts fall within the critical period for cataracts, 4-8 weeks, and none of them outside. But that’s probably more likely than it sounds (looking at weeks 1-12 on figure 2, getting within weeks 4-8 is a 5/12 chance or 0.417, and–given three such weeks–getting them all in that window is a chance of 0.072, but for four different birth defects, the chance of getting one hit randomly is a less impressive 0.29. The calculation is more complex allowing for different numbers of weeks showing significance within the critical period, and allowing for the fact that heat wave were defined as three successive days over the 90th percentile in temperature. Also, we don’t actually know the sensitivity for congenital cataracts for for each week in weeks 4-7, so calculating the odds of getting figure 2 by chance becomes impossible.
The point about comparing populations in warmer climates with the study group is a good one. I would add, though, that our ability to deal with heat does include both some genetic basis, and some acclimation. The authors quoted animal studies on hyperthermia causing birth defects, though now, I’ll apologize for not taking the time to look them up and find out how extreme that hypothermia was. Also, hyperthermia itself might not be the causative agent; stress hormones or other reactions to unaccustomed heat might be involved as well. Just to muddy the waters a bit…still, my opinion of this paper has dropped.
Regarding the Monte Hall problem…the best way to understand this is to simply draw out a decision tree. You pick door #1, with a 33% chance at the prize. Game show host then chooses door #2, which is not the prize. 0% chance. Door #1 is still 33%, so door %3 must have a 67% chance of having the prize behind it. Sounds bogus. But draw out each possibility, e.g., say the prize is behind door # 1. Pick door 1, see door 2, stay with door 1. Pick door 1, see door 2, change to door 3. Pick door 1, and this time, see door 3, with 2 choices. Then, pick door 2 and look at those choices. Multiply through the probabilities for each. Then, for all the winning paths (door with the prize and door you end up with are the same) add up the probability for that path, calculated as the product of probabilities for each step. When this hit the news, because a columnist had commented on it, I was sure it was wrong. My brother, who was a math grad student, told me to try drawing out that tree-structure of probabilities. He also told me that he’d tried this with the students the college algebra class he was teaching, with playing cards, and, in over 100 trials, it came out pretty close to 1/3 wins if you stayed with your first choice, and 2/3 wins if you switched.
I finally got it, and I was really annoyed that he’d gotten one up on me. At the time, I’d just typed in a random number generator into the computer (from Marsaglia and co-authors, as it happened) to use for a Monte Carlo program** I was modifying and testing. So, just to outdo my brother in some way, when I left the bar, I wrote a quick program and tested the Monte Hall effect (in a very simple Monte Carlo simulation) over five million trials.
Well, whatever else its failings, this paper’s given us an interesting thread.
[**Monte Carlo simulation involves exploring a simulated system or solving complex equations using many random trials. A simple example would be estimating the area inside some region by defining a rectangle containing that region, then looking at many points within the rectangle, The fraction of points falling in the region gives its area relative to that of the rectangle.]
Not been on this before, but what a great range of comments in this thread. One of the really nice things was the humility of rgbatduke – someone who clearly is comfortable with the use of statistics, remarking on what he does not know. It’s sad to note though that folks who don’t come anywhere near his level of expertise are able to pass themselves off as statistical experts, and so our society is being shaped in so many ways by those who abuse their level of knowledge – the AGW scam, passive smoking, efficacy of drugs, you name it, our society is being shaped by those who are abusing their knowledge in some way. I’ve gone through university in the UK – did various degree courses (biochemistry, public health engineering) in which statistics was always a part. But I never paid any attention to the stats part of the courses, simply because in my final exams, stats would usually get maybe one question out of 8, and I could rely on my choice being reduced to answering 5 out of 7. So I always ignored stats – until I did an MBA, there was no getting past it, I finally had to knuckle down. What I remember from that is enough to know that usually I don’t know – so I’d like to think I’m in the group who know enough to know what I know but more importantly, know what I don’t know. As the general population is made up of people who don’t know that they don’t know stats can be abused without fear of comment. And our society is very much poorer for it. Environmental groups can frighten folks with claims that are simply preposterous – and few ever question them. They are the new gods of information, held in high esteem by the general population all over the world, yet they are mainly charlatans, selling quack medicines. With the dumbing down of education here in the UK, things will only get worse. I cannot see any change at all – not until university courses are organised so that stats is an integral part of every question – no escape; and basic stats is taught as a “must do” subject in every school. Probably will never happen. So good luck guys, in your quest as the voices of reason and truth, but I fear you are both literally and figuratively tilting at windmills.
It’s seems a strange conclusion, even without dredging the data for correlations. These were *unborn* kids supposedly affected. During their gestation, where they were was thermostatted far more precisely than any conventional environmental control system. That’s the advantage of being internally gestating homeotherms.
Or are there Burroughs’ Martians among us?
Monty’s not opening the doors randomly. He’s opening them because he knows they don’t contain the zillion samolians. Each empty door he opens gives you a little more information than you had when you made your original choice. If he were opening them randomly, your gut would be right.
And Bayes theorem and information theory are one and the same thing, in the end. Information is the key. Monty can actually open any of the doors that (he knows) do not contain the prize randomly (if there are more than two), it won’t matter. But he cannot open a random door out of the set of unchosen doors, because then it might contain the prize. We learn a bit more of what Monty knows with every door he opens, and it shifts our odds if we use the information. But this is hard to understand, so let’s work it out. It’s not too difficult.
Here’s a very simple parsing of the chances. When you chose between the 3 doors originally, you had a 1 in 3 chance of guessing the right door. Each of the other doors also had a 1 in 3 chance of being right, so 2 out of 3 times you guessed wrong. Monty opens a door and reveals it to contain a year’s supply of dogfood — and a dog — not the two week vacation in Tahiti. The door you selected has a 33% chance of being right, but the other door has a 100% chance (now) of being right — 67% of the time.
Better to switch, don’t you think? Unless you cherish the barbecue grill and year’s supply of steaks that is the other “junk” prize.
The key thing is to realize that the second “trial” is not independent of the first, so you have to deal with conditional and joint probabilities, which is what Bayes theorem is all about.
Note well that this is defeated if Monty is permitted to choose whether or not to open a door. For example, he could open a door only if you’ve chosen the actual prize to entice you to switch — this is actually not crazy, maybe the company likes to conserve valuable prizes. So if he knows you have chosen correctly, he opens a door to entice you to re-choose (assuming that you are a good statistician and know that you “should” double your chances by doing so, but if you have chosen incorrectly he always goes ahead and reveals the dogfood you’ve chosen. Ouch. You win only if you always stick, 1/3 of the time, and even less if you are enticed into switching — you win 0% of the time if you always switch.
This opens up a whole range of games Monty can play by rarely opening a door when the prize is on his side even if you’ve lost, so that you learn that there is some chance of winning. Most of those games (if played perfectly) would increase your optimum yield from 1/3, but now we’re well on the way to inventing rock-paper-scissors games, where the optimum strategy is to guess completely randomly (and win on average half the time) but where humans can often nevertheless exploit information theory and beat the hell out of their opponents when neither side chooses randomly. Humans have a hard time CHOOSING randomly without using dice or coin flips — what we intuitively think of as being a “random” sequence almost never is.
rgb
You will always have better odds switching, the greater N is the greater the advantage to switching.
Well, not quite. Your original choice was 1/N. The chances that it was behind one of the other doors is (N-1)/N. One door on the right is opened. If you choose from the remaining unopened doors, the chances are now 1/(N-2) of winning if you reselect from that side AND the prize is there. The chance of winning is thus the product: p(switch and rechoose) = (N-1)/N-2) * 1/N (for N>2 for this to make any sense). For N=3 p(s&r) = 2/1 * 1/3 = 2/3, double your original chance.
For N =4 p(s&r) = 3/2 * 1/4 = 3/8, or 1.5 times your original chance.
For N = 5 p = 4/3 * 1/5, or 1.33 tiems your original chance.
For N=1000, p = 999/998 * 1/1000, hardly worth it to switch.
So the MAXIMUM advantage to switching is exactly N=3.
rgb
It’s seems a strange conclusion, even without dredging the data for correlations. These were *unborn* kids supposedly affected. During their gestation, where they were was thermostatted far more precisely than any conventional environmental control system. That’s the advantage of being internally gestating homeotherms.
Or are there Burroughs’ Martians among us?
It isn’t that simple. There is substantial, convincing evidence with p much smaller than 0.05 that fevers during critical periods are correlated with the defect, where it is more likely the fever per se that is the cause and not the virus or other cause of fever because it is positively associated with the fever caused by MANY diseases, not just one or two.
It is also certainly a true fact that prolonged exposure to very high outside temperatures with inadequate shade, water, and/or too much humidity so sweating doesn’t work to keep you cool can lead to hyperthermia, where your internal body temperature creeps up over its “normal” set point because you literally cannot throw off heat fast enough. When the temperature outside is 100F, for example, you are trying to cool into an environment hotter than you are, which REQUIRES sweating profusely. One can literally overwhelm one’s natural thermostat, leading to heat exhaustion and heat stroke as your body’s internal temperature rises to 102F and then to 104-105 F, where your brain basically malfunctions and you have strong odds of straight up dying.
It is therefore a reasonable hypothesis that environmental hyperthermia during pregnancy could lead to birth defects, this particular one among others. As I pointed out, neural tube defects are the most likely ones to first observe as they are most strongly correlated with fever-induced hyperthermia.
However, this is a long ways away from showing that pregnant women have a high enough chance of experiencing actual internal hyperthermia to affect birth defect rates by increasing them by 50%. That is, in fact, close to absurd. It takes time and a certain amount of abuse or stupidity to experience hyperthermia, as we naturally seek cooler environments and cool drinks when it is hot out. One needs MOST of the women in question to have spent long times outdoors, not drinking, and consequently overheating to the point of having the equivalent of a low grade fever. Maybe, but I doubt it, and if so why weren’t neural tube defects spiked first?
Bayesian analysis of neural tube defects and other disorders related to fevers suggest that the hypothesis is probably false, and in any event is marginal on the data, especially when it is a dredged conclusion.
rgb
Mr Briggs has just swatted this piece of trash into the round file….:
http://wmbriggs.com/blog/?p=6870
The most common cause of cataracts in infants is being kissed on the eyes by a parent with a herpes outbreak or “cold sore” on their lips. Source: “Herpes: What to do when you have it” by Dr Oscar Gillespie
E.M.Smith says:
Another case of “Climate Science” done by folks who took one Stats class, then forgot most of it.
Possibly they had a similar level of education in biology. Or are just unable to think through the logic of humans being placental mammals.
One nit — The 75% chance is for any study that has 28 different data dredges going on. There is not a 3/4 chance that any one of them will be.
If 10 different studies of this sort were done, 3 out of 4 would get a positive result.
Another NIT– The problem with these studies in general is that they study the dead and ignore the living. Instead of looking at the percent dead, look at the percent living.
(You have to be able to equate dead with ‘having cataracts’ and living with ‘not having cataracts’)
Studies like this focus on the small numbers on the dead end of the spectrum and fail to consider how it is that so many people manage to avoid getting cataracts having been exposed to the same conditions.
Smokers have 25-40x risk of getting lung cancer because they smoke. This also means that there is a 92% chance that in 60 years of smoking they won’t get lung cancer. There are a few rational epidemiologists out there. Unfortunately epidemiologists are sort of like lawyers, we have way more of them than we need.
To stay employed though, they need to do work. Hence we get this stuff.
The great irony of epidemiology is that the valuable work the do is not in the positive correlations they find. It is in the negative. All the results that say “no correlation” are the ones that are meaningful. (There are a few rare exceptions, smoking/lung cancer, oral sex/Oral cancer[caused by HPV]).
“I have to confess, I laughed out loud when I read the study.”
As I did with your title. Knew exactly who wrote it before looking.
Was getting a bit worried of late that Willis hasn’t posted for a while – welcome back. I always enjoy a good read.
michaelozanne says:
December 21, 2012 at 10:08 am
“Mr Briggs has just swatted this piece of trash into the round file….:”
Hmm. Briggs talks about “…presence or absence of 84 different birth defects…” and also “…for a couple of the 84 birth defects….”
There were 84 comparisons, but for 28 birth defects, with three indices of heat as causes. One of these could be a typo, but when he repeats it, this raises a question about how carefully he read the paper.
In a sort of similar vein: in the paper, they stated: “We found positive and consistent associations with congenital cataracts of multiple ambient heat exposure indicators, including 5-degree increases in the mean daily UAT (minimum, mean, and maximum), a heat wave episode, the number of heat waves, and the number of days above the 90th percentile of UAT.”
Now, I don’t think it useful to go calculating the probability of hitting on all three indicators by chance, since the three indicators should be highly correlated.. But it does seem to indicate that dividing the 5% criterion by 84 may be too conservative. If you pick any one of the indicators, the cataracts come out statistically significant. Perhaps it might be more realistic, in this case, to divide bu 28 instead. The presumed high degree of correlation among heat indicators would actually support this, since it means they weren’t really doing 84 independent correlations. I suspect that there must be some way of dealing with this, although the authors may not have known about it.
They mention cataracts being associated with the number of heat waves and the number of days above 90th percentile of UAT, That actually looks to me like a dose-response relationship, which is definitly stronger evidence than a simple statistical significance for incidence. But they give no details so it’s hard to tell. If they really saw a dose-response relationship, it would seem strange that they didn’t mention it.
rgbatduke says:
December 21, 2012 at 8:15 am
Or perhaps the rate is actually higher among women more exposed to heat, but the study was diluted by women who didn’t get overheated Perhaps some were better adapted to heat due to genetic background. Perhaps only a few women worked outside or inside without air conditioning, didn’t have it at home, and were constitutionally less able to withstand these conditions.
From the paper:
So, at least they considered some explanations for the lack of neural tube defects showing up.
So, quick google scholar search on animal studies for neural tube defects:
http://content.karger.com/ProdukteDB/produkte.asp?Aktion=ShowAbstractBuch&ArtikelNr=242767&ProduktNr=247786
http://onlinelibrary.wiley.com/doi/10.1002/tera.1420290313/abstract
http://onlinelibrary.wiley.com/doi/10.1002/tera.1420310212/abstract
These first three abstracts I got back (articles paywalled) showed one that counted prenatal death, one that considered it, and one that didn’t mention it (although the paper could have). So, perhaps the fact that they couldn’t track prenatal deaths might have some bearing on the question neural tube defects.
Another point: these mouse studies looked at severe temperature elevations, perhaps as much as 5-6 deg. C, which would stand a good chance of killing a human. Then again, there may be birth defects in mice with milder heating, but at a rate difficult to see without an enormous study.
Also, the lens of the eye is a strange beast. It is the only human organ for which occupational exposure to radiation is known to have deterministic rather than stochastic effects. Get enough radiation exposure, and you WILL get cataracts, whereas you MIGHT get cancer (and your chances of that, as a radiation worker working within the occupational limits are pretty low).
Articles on this are harder to find but this one
http://onlinelibrary.wiley.com/doi/10.1111/j.1741-4520.1996.tb00316.x/abstract
mentions finding changes in the lens of fetal guinea pigs subjected to hyperthermia, that could show up later in life as cataracts, and also induction of cataracts at different stages of pregnancy (though most strongly in early pregnancy, when the eyes would be forming).
Given this, it’s plausible that pregnant women exposed to mild hyperthermia for days on end (slowly building up tissue damage) might have offspring with more cataracts than neural tube defects, whereas for more acute exposures such as fevers, this would be reversed. This would be because the lens can accumulate subtle damage over time, at least for radiation. The neural tube closes, or it doesn’t, over a relatively brief time.
All of this together doesn’t make the paper believable. I think it tilts the odds in that direction a bit. If there turns out to be something going on here, it’s good to know for a few reasons. MRI scans used to be contraindicated for pregnant women, since the effects of the slight heating from the RF (I think about 1 deg..C) were unknown. Extra knowledge is always helpful. Still, there are a lot of reasons why waving this paperaround in relation to global warming is pretty silly: the results are uncertain, to say the least; they indicate, if anything, something that’s probably a rare problem, and people who get frightened from something like this won’t be considering things like adaptation to a warmer environment. Maybe they will eventually start giving stronger warnings to pregnant women to avoid overheating. I somehow sense that they are already doing this themselves.
http://imgs.xkcd.com/comics/depth_perception.png
JazzyT, you say:
JazzyT, you are wrong. The cataracts are not statistically significant, because they were found as the result of a data dredge. It doesn’t matter whether you look at it as finding 5 “significant” results out of 84, or 1 or 2 “significant” results out of 28 makes no difference. For N=84, we expect 4 false positives, about what we got. For 28, we also expect about what we got., 1 or 2.
In other words, the results are EXACTLY AS EXPECTED FROM RANDOM CHANCE. This means it is incorrect to say that “the cataracts come out statistically significant”. They do not.
You go on to say:
You’re missing the point. We don’t have a scrap of evidence that any of the women overheated at all. It would be surprising to me if they did, at least if my wife’s behavior when pregnant is any guide. She was sensitive to heat, and wouldn’t go out in it unless she had to.
Note that we’re not talking about simply getting hot. For their theory to work the women would have to have suffered hyperthermia, where the body temperature actually rises … and we have no evidence that they did that.
But without actual evidence, they are just blowing smoke. Without actual evidence, speculating about whether “some were better adapted to heat” goes nowhere. Without actual evidence, we know nothing. Without actual evidence, their study is meaningless.
Plausible? For it to be “plausible”, you’d have to have pregnant women being “exposed to mild hyperthermia for days on end”. How on earth is that supposed to happen? Our bodies are exquisitely tuned to keep the body temperature within a very narrow range no matter the environmental temperature. You are describing pregnant women running a 1° or so fever for days and days … how is that “plausible”? Sounds highly improbable to me.
You close by saying in part:
Sorry to be so blunt, but the paper is trash. It has no evidence, it is a data-dredge between the temperature at the nearest airport and birth defects. There has been no physically plausible mechanism suggested whereby a “heat wave” would raise the temperature of the fetus. In fact, there is no evidence that the women have even experienced excessive heat at all.
As a result, I have no idea what could “tip the odds” in favor of the paper being believable. It is evidence-free and statistically ludicrous, no matter how you tip it …
w.
I’d say that a statistical study on statistics would probably show that, as a statistical average, people are not very good at statistics.
Mero, you wrote, “I’d say that a statistical study on statistics would probably show that, as a statistical average, people are not very good at statistics.” Yep. 9 out of 10 are definitely below average…
;>
MJM
Merovign says:
December 22, 2012 at 2:32 pm
One of the tragedies of the world is that if you ask someone how intelligent they are, most folks will say “a little above average”. It’s almost magical how there is a perfect inverse relationship between actual intelligence and the self-estimation process, with the balance so exact that everyone ends up a little above average.
Unfortunately, if you ask a climate scientist how good a statistician they are, there’s a good chance you’ll get the same answer.
I am by no means a journeyman statistician, my knowledge is wider than it is deep, I defer to Dr. Brown from Duke University (posting as rgbatduke) for that, heck, someone corrected a couple of my statistical errors upstream … but I am smart enough to recognize a data dredge when I see one.
w.
OK, first, I’m not actually trying to save this paper, I don’t think that much of it. But, I’m not absolutely certain that it was a waste of (probably public) money, either, especially since reporting weak or negative results lets other researchers decide whether they might want to follow on or not. But any publicity that this paper gets regarding global warming is just silly, and reflects, among other thins, a slow news day in the warm zone.
Having said that, I do like learning new stuff, and I do tend to try to avoid being to certain about things–such as “this paper is useless”–until I’m justified in being sure about it.;
Willis Eschenbach says:
December 21, 2012 at 11:54 pm
My bad. I gave the argument and neglected to say what the real point was. I’d like to quit posting right around sleepytime, but that’s when I can grab some free time.
I was talking specifically about applying the Bonferroni adjustment, mentioned in the paper and also above:
Lance Wallace says:
December 20, 2012 at 1:04 am
I hadn’t actually picked up on Lance going with 28 comparisons instead of 84. As he said, we want to look at 28 different comparison, but with only a 5% chance of even one of them being a spurious correlation. We’ll use the equation you started with:
FP = 1 – (1 – p)^N
If you want to avoid even one false positive at the “p” level, you divide p by N, for
FP = 1 – (1 – p/N)^N
Rather than write this out in all its gory glory, we’ll just give the answers for N=28 and N=84.
For p=0.5 and N=28, the false positive rate FP = (1-001786)^28 = 0.9512
For N= 84 we get p = 0.9512 again.
You end up with a chance that’s actually slight less than 5%, though only very slightly, that even one correlation is a false alarm I’d never heard of it before this conversation. But yes, it’s actually possible to go data-dredging and get meaningful results, as long as it’s done properly. (It helps if you have meaningful background information.)
It”m not sure whether the usual terminology for the data dredge without Bonferrroni corrrecton would be “not statistically significant” or “statistically significant, but meaningless.”
Welcome to epidemiology! Without a huge amount of resources, you can’t do things like track down individual women and ask them if they remember hypotherma during a years-distant pregnancy. Some unkonwn percentage of those who didn’t actually collapse might not remember anyway. A (much more expensive) prospective study would give better info by letting pregnant women keep journals, or something, but at a much higher cost.
You don’t spend a lot of money on a big study until little studies like this one tell you whether it’s worth doing. So instead of implanting a radio-telemetry thermometer in each of 10,000 pregnant women, or even something far less preposterous but still expensive, you make do with whatever you can get. When you don’t have data, you use proxies–like the temperature at the nearest airport. If that tells you something interesting, then you go for the big-money studies.
A sample size of one…but, I’m glad she had the sense to come in out of the heat. Not all women have that option. When I was a teenager, I worked on a farm during a couple of summers. (I was too young for other full-time work.) Our crew took on a family with parents, young kids, and a very visibly pregnant teen daughter. She didn’t do much work–always complained about the heat. about her husband being in prison, and kept saying, “Mama, I wanna go lay down…” She did what she could to avoid heat stress, and Mama did let her lie down in the shade sometimes, but none of us were really able to get out of the heat of a Southern (US) farm in summer.
Another sample size of one, but your wife, and that poor girl (her family was very poor) represent two ways things can go. In a lot of places I’ve lived, when there’s a heat wave, they put out warnings on the radio and TV to go check on neighbors or others you know, and I’m very used to hearing a small death toll for the really severe ones. Even in some hot areas, not everyone even has air conditioning. In the cities, people have been known to sleep on the fire escape, and they put sprinklers on fire hydrants for the kids, but there’s only so much you can do.
Welcome to epidemiology…when you can’t yet afford direct data, ya gotta use proxies, with all their limitations. We don’t know how many women suffered heat exhaustion or heat stroke, but with a sample size of 6,400 (and a control group o 59,000) it probably wasn’t zero. I’m sure the authors had access to data on incidence rates.
Just for fun, I started fooling around with the confidence intervals on the congenital cataract data.I applied Bonferroni adjustment for N=28, on the theory that max, min, and mean temperature on really hot days ought to be correlated. They mentioned that with the Bonferroni adjustment for N-84, they would not be statistically significant at the 95% level. For N=28, they were not either, though they would have come closer. For one dataset, (minimum daily UAT) actually looked at the p-value required to hit 1.0 for the lower bound on the confidence interval for the odds ratio. For a two-tailed test, p=0.964, so it fails a two-tailed test at 95%, but would have passed a one-tailed test. I suspect that this would be true of the others as well.
All this was done with the assumption that the logarithm of the odds ratio would follow a normal distribution, as is, well, normal, and looking up cumulative probabilities for various Z values, rescaling things as necessary. I can post more details if anyone REALLY wants them.
All of this doesn’t make me like the paper. But I used to date an epidemiologist, and I gained a lot of respect for a field that was much more complicated, capable, and important than I’d ever known. She wasn’t doing cataracts and heat, she was doing causation studies and clinical trials for cancer and AIDS. She was quite skeptical of some of the science she saw. From her, I found out just enough about things that looked good and weren’t, or looked bad but weren’t, that in order to pass final judgement on a paper like this, I’d want run it past a trusted expert, like her.
And again–it’s just silly that a nebulous piece like this, that is at best preliminary, should be touted as showing adverse health effects of global warming–without noting that the paper is uncertain at best, and even the results panned out with a bigger study, that people can and do adapt to temperature changes, and that, in the end, surgery to correct cataracts exists, and is mild in comparison to fixing, say, spina bifida.
On the other hand, now I know a couple of things about stats that I didn’t know before, and I’m definitely good with that.
Well, the people in India have the highest cataract in the world. Due to radioactive exposure one assumes from the slide of India into Asia releasing deep gases from the interior like radon.
Did you notice that even tho the UN experiment with high Vit A supplement going bad ( the children got cancer) the push for added Vit A to rice is back?
You end up with a chance that’s actually slight less than 5%, though only very slightly, that even one correlation is a false alarm I’d never heard of it before this conversation. But yes, it’s actually possible to go data-dredging and get meaningful results, as long as it’s done properly. (It helps if you have meaningful background information.) C, or
C, or 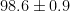 F. There is an entire wikipedia article on it. It is typically lowest around 4 a.m. and highest around 4 p.m. A temperature of 99.1 F might be considered evidence of a fever in the early morning but not in the mid to late afternoon. These temperatures also vary with activity, e.g. exercise. In fact, the wikipedia article:
F. There is an entire wikipedia article on it. It is typically lowest around 4 a.m. and highest around 4 p.m. A temperature of 99.1 F might be considered evidence of a fever in the early morning but not in the mid to late afternoon. These temperatures also vary with activity, e.g. exercise. In fact, the wikipedia article:
JT, I largely agree with your modified comments above — and made many of the same points. There is a “proven” association between fevers, at least, and a variety of birth defects. It is perfectly reasonable to ask the question: “Is environmentally induced hyperthermia a plausible cause of some of the birth defects known to be plausibly caused by fevers?”
However, you still miss one of Willis’ (and my) main points. This is not what they investigated. They investigated — data dredge style — whether or not there was any correlation between airport temperatures in the general vicinity and not one but a vast array of possible defects. Now, what do you think you would observe if you had a thermometer embedded inside your gut over the course of a day?
The answer is that the thermometer would read — under normal circumstances —
http://en.wikipedia.org/wiki/Human_body_temperature
lists not one but many factors that affect body temperature. Food, drink, tobacco, clothing, exercise, sleep cycle, psychological stress, and alcohol consumption all affect body core temperature. Sleeping under an electric blanket is known to raise nighttime core temperatures as well. Pregnancy was not listed as a risk factor for hyperthermia. That isn’t to say that it isn’t — indeed, the following article:
http://www.ncbi.nlm.nih.gov/pubmed/16933304
suggests that “an episode of hyperthermia is not uncommon during pregnancy” from all causes already and yes, this article does directly study the consequences, with neural defects prominently leading the way (not just one, but many, and in humans, not just animal models). It also specifically looks at episodes of hyperthermia (as well as fever) in pregnant women, not at “heat waves” at a nearby airport.
Medical hyperthermia occurs when the body produces more heat than it can dissipate. This can happen by increasing production — exercise, eating, drinking warm or stimulating liquids — or by interfering with the body’s heat loss mechanisms e.g. wearing sweatsuits to exercise in, spending a long time in very hot/humid conditions without drinking plenty of fluids and sweating. It leads to what we consider “heat exhaustion” — headache, confusion, fatigue — associated with a 1-2F increase in body temperature (about the same as a mild fever of 101-102 F). If left untreated, it can progress to heat stroke when body temperatures elevate to 104-105 F (about the same sort of fever one gets from serious diseases, e.g. malaria). Malaria used to be one of the few known cures for syphilis as the high fever it produced was fatal to the syphilis spirochete. Of course, you had to survive the malaria…
All of these factors are profound and unconsidered confounders in this data-dredge study. Consider — are birth defects rates correlated with keeping your household thermostat set high? Sleeping under an electric blanket if pregnant? Exercising during pregnancy (which would be by far the biggest risk factor, right)? Working outside picking cotton or harvesting fruits and vegetables in midsummer while pregnant? Living in Florida? Being fat (because fat is a good insulator and ready source of energy and requires more metabolic core expenditure to move around)? Because I would bet that there are plenty of fat female migrant workers who live in Florida and pick vegetables in midsummer while pregnant or who live in tent camps or non-air-conditioned trailers while their husbands work — are they an undetected epidemic of birth defects, and if so could we distinguish the defects caused by heat from those caused by exposure to e.g. toxic pesticides?
In order for this study to even think of having meaning, one would have to prove an association between airport temperatures and specific episodes of hyperthermia in pregnant women. It does not even try to assert a specific relationship between outside temperatures and episodes of hyperthermia in pregnant women. It leaves it to the imagination!
Is this science? It is not. B is known to be correlated with C (hyperthermia with birth defects) in a certain spectrum. A is hypothesized to be correlated with B (high airport temperatures cause hyperthermia in pregnant women). Instead of studying the relationship between A and B, study the relationship between A and C (assuming there is a relationship between A and B, as it were). Even then, observe precisely the distribution of correlations between A and C that one would expect from random chance (see the xkcd comic I posted up above, seriously — it says it all, screw “corrections”). Pick the most extreme of these, claim a possible causal relationship.
What have they proven? That high airport temperatures cause hyperthermia in pregnant women? Surely there are easier and more direct ways to prove that, and this is the only plausible causal connection between high airport temperatures and hyperthermia-induced birth defects!
In fact, given actual knowledge of the connection between hyperthermia and fever episodes and birth defects, one has only to study the incidence of episodes of clinical hyperthermia with outside temperature to be able to predict the expected increases in birth defects, is that not correct?
This was not done, and it was the first thing that should have been done. Then they could go further and try to associate specific episodes of hyperthermia that are actually caused by the heat wave with specific birth defects and maybe — just maybe — they’d get an association. But not with only 60,000 samples. That’s too small to get good numbers with a 0.0004 baseline prevalence. If they had 250,000 samples, all randomly drawn (we can talk about bias another time) then they’d expect to get around 100 of these particular birth defects “normally”. They then might be able to resolve the effect of specific episodes of hyperthermia on the birth defect, and would be left only having to prove a bump in the rate of episodes of hyperthermia during heat waves that corresponded accurately with the bump in this birth defect, and explain why all of the other defects studied had a null result!
Why was it only the green jellybeans that caused acne? Why not the blue, purple, mauve… ones?
There is a lovely book that you should all buy and read, called “How to Lie With Statistics”. It was written in 1952 by Darrell Huff. It is not heavy math — it is easy to read and very short. It walks one through how even well-meaning people with an axe to grind mispresent statistics in countless ways to deliberately or accidentally mislead their audience towards a desired conclusion.
These methods are in common use in climate science today, starting almost on page one — confusion of the three types of “averages” that can be presented as an average. In climate science this issue is enormously apropos as it is all but impossible to cleanly define or measure the mean enthalpy content of the Earth as a function of time. The Earth’s mean temperature is presented to two decimal places — another way of misleading discussed in the book (and used by e.g. Karl Marx with great effect). The “Gee-Whiz Graph”, however, is one of the major weapons. For example, leaving out the base and plotting only the variance (a.k.a. “the anomaly”) on a scale that arbitrarily distorts the size of the variation compared to the actual total value, on a range that happens to be the range that allows one to argue for the conclusions one wishes everybody to accept. The Darkening Shadow (map manipulation) is commonplace — painting Antarctica red. And of course, Post Hoc Rides Again (these are chapter titles), as in this study — he doesn’t explicitly describe data dredging, but he does point out that correlation is not causality.
This study is a pure data dredge. It doesn’t even study the right relationship, the one that actually would establish the right correlation from which the inference could reasonably be made, and it obtains a result precisely as meaningful as the green jellybeans cause acne example, right down to the headline at the end! The media loves to statisculate (term defined in book) because boring null statistics don’t sell the news. Two newspapermen caused an entire crime wave back in Theodore Roosevelt’s day, just by reporting every crime that occurred, no matter how small. The actual crime rate hadn’t changed — only the attention of the media — but people went in fear of their life and property.
How to Lie With Statistics should be mandatory reading in every intro stats class. It is actually more valuable to read it, for the ordinary human, than learning all about means and standard deviations and Student’s T and so on. Of course, a lot of people have a good feel for it as part of their sheer common sense. Joe the Cab Driver in Taleb’s equally awesome book, The Black Swan, understands this. Joe is a natural Bayesian.
BTW, your computation of 5% being “barely” wrong is incorrect. It is way off. This result is completely insignificant when viewed globally, precisely as is the case with green jellybeans.
rgb
rgbatduke says: @ December 23, 2012 at 6:40 am
….There is a lovely book that you should all buy and read, called “How to Lie With Statistics”. It was written in 1952 by Darrell Huff…
>>>>>>>>>>>>>>>>>>>>>>>>>>
I will second that suggestion.
After reading that book you will never look at a poll splashed all over the newspapers or a ‘Scientific study’ quite the same way again and you do not have to be a math wiz to understand the book.
It should be a must give to every high School student on your shopping list.
JazzyT, you discuss the Bonferroni correction. Your conclusion is as follows:
As I said, I’m not a journeyman statistician. And I, like you, had never heard of the Bonferroni correction, but I think that you have the stick by the wrong end.
The Bonferroni correction is an approximation. It is a correction such that
1- (1 – p/N)N ≈ p
for small values of p, regardless of the value of N
For example, for p = 0.05, you get 0.05 with N =1, and with p = 0.05 and N = 100 you get 0.049.
This doesn’t mean what you think it means, though. You think it means that in the data dredge, the cataract result at p=0.05 is significant. The correction works the opposite way.
It means that if you are looking at 28 results, in order to consider your data dredge as a whole to have yielded significant results at the p = 0.05 level, you need to find an individual result that is significant at the level of p divided by N, which is 0.05 / 28 = .003. As far as I know, the authors did not find anything approaching that level of significance.
As I mentioned, the Bonferroni correction is an approximation. It is a lovely and very accurate one for our normal range of interest, say from p = 0.05 and smaller. At p = 0.05, the error even with N = 100 is quite small, about 0.001.
At p = 0.5, on the other hand, the error with N=100 is about 0.1, not bad I suppose. The good news is that we never do probability calcs in that range of p-values, so it doesn’t matter. The Bonferroni calculation is a neat trick to approximate the p-value that you would need to declare a data dredge successful … I’ll remember that one.
A huge problem is that the data dredge is often invisible, because it is not all done at once. It may occur over some months. It is then dismissed as something like “the understandably long process of looking for a small signal that is difficult to find and isolate”.
Fair enough. But after someone has looked for the infamous “anthropological fingerprint” in enough obscure corners of the climate, they can’t just declare success because the results for the positive correlation they finally found have a p-value of 0.05 …
This is particularly epidemic among people looking for astronomical correlations with the weather. They search for relationship between the global temperature or some other climate variable with things like the synodic period of Jupiter and Saturn or the intervals between the nearest approach of the moon to the earth. Far too often, someone spends months looks through literally dozens and dozens of these correlations, and then finally finds a result with p = 0.045, and declares that it is significant.
This is one reason I very much dislike the significance level being taken as p = 0.05. That means you’ll find a false positive one time in twenty. If you look at as few as a dozen possible correlations in search of the real one, you have nearly a 50/50 chance of having a false positive.
If you take P = 0.01 as being significant, on the other hand, with a dozen possible correlations you have only a 11% chance of a false positive. So you are better insulated from the data dredge, with a dozen possible correlations you have an 11% chance of a false positive.
w.
Couple of things:
1) I’d add Joel Best’s “Damned Lies and Statistics” to the “How to Lie…” book recommendation. And if you get his sequel, “More Damned Lies and Statistics” you’ll even find an example about rabbits and Antismokers I’d recommended to him in an email! 🙂
2) RG, you said, “Now, what do you think you would observe if you had a thermometer embedded inside your gut over the course of a day?” Back when I was young and hypochondriaciacal (Ok, ok, not a word, but it works.) I went through a period of worrying that I would die in the wee hours when I’d take my temp and find it down around 96 degrees. :> Guess I’m just a cold-blooded guy.
:>
MJM
At p = 0.5, on the other hand, the error with N=100 is about 0.1, not bad I suppose. The good news is that we never do probability calcs in that range of p-values, so it doesn’t matter. The Bonferroni calculation is a neat trick to approximate the p-value that you would need to declare a data dredge successful … I’ll remember that one.
Also consider actually looking at the distribution of p. This gives you some very useful information. For p to have any meaning in the first place, the “mean results” one is studying have to be Gaussian, that is, the central limit theorem has to have kicked in. In that case, if the null hypothesis is true, the distribution of p should be uniform — your experiment is a very odd kind of a random number generator, because it is a projection of the two-sided complementary error function, the inverse of the gaussian distribution. This is a function that is one when the value occurs at the centroid of the gaussian around the (null hypothesis) expected value and decreases to zero when one reaches the wings. It is this kind of thing one is implicitly referring to when one talks of 0.05 in the fist place — it just means that the result is two standard deviations from the mean, and has enough data that you have “confidence” in it.
But are the results normal? Is p distributed uniformly? Can one distinguish p from a uniform distribution with e.g. a Kolmogorov-Smirnov test? A histogram of p-values from the study could be very revealing. If it were egregiously non-flat it would suggest that either their hypothesis concerning “confidence” is false, that there really isn’t enough data in the study to have much confidence in it (something I suspect is the case) or that the null hypothesis is false and there are correlations on a broad scale. However, figuring out which would be difficult without simply making the study four or five times as large and fixing the flaws.
rgb
Back when I was young and hypochondriaciacal (Ok, ok, not a word, but it works.) I went through a period of worrying that I would die in the wee hours when I’d take my temp and find it down around 96 degrees. :> Guess I’m just a cold-blooded guy.
96 is probably a bit on the low side, but there is considerable variation depending on where and how you measured your temperature, the precision of your instruments, and from person to person. That’s another kicker. We haven’t even touched drugs or foods that can affect body temperature, how your cardiovascular health affects your body temperature, how much natural variation there is in body temperature. For example, 98.6 plus or minus 0.9 degrees — what exactly does that 0.9 degrees stand for? A Gaussian standard deviation? An absolute range with or without some skew? Somewhere somebody may have had people swallow button recording thermometers, or stuck them up their butts or fastened them inside a cervical cap and had them wear them for weeks and then read off the results, and somewhere out there in the Universe of data one can probably find real time temperature vs time for 1000 people over twelve months and some variation in conditions. This is the sort of thing that is needed as a Bayesian prior for this study.
There are some very nifty recording thermometers available at this point — I looked into them extensively a decade ago when trying to think about clever ways of monitoring computers in server rooms. One really could attach a button device to the end of a tampon and measure not only core temperature, but core temperature right next to the womb in pregnant women, if you could find somebody willing to risk doing ANYTHING with pregnant women that COULD cause a miscarriage or whatever. That would give you some seriously useful information.
rgb
For applyinh the Bonferroni correction with 28 correlations,
Willis Eschenbach says:
December 23, 2012 at 5:02 pm
As far as I know, the authors did not find anything approaching that level of significance.
(5/28 = 0.018, but no matter here…)
Actually, what I’m saying is that they did get close to that level of significance, but they don’t seem to have realized this. It takes a few derivations to find out. Essentially, you move the ends of their confidence intervals from the p=0.05 level out to the p=0.05/28 level.
So, some about this article, but more about such studies in general:
It’s true that to draw really believable conclusions about about heat waves causing birth defects, you need to connect the dots to find out who was exposed to hot temperatures. Finding out who actually had an episode of hyperthermia may or may not be of interest depending on the study, since population effects of environmental stressors actually is a valid thing to study., Looking at the individual establishes the causal chain more rigorously, and that’s a different, but important study if you’re looking at important effects.
It looks like this was a pilot study, aimed at getting preliminary data for a grant proposal. All the data used were available as relatively simple records: airport temperatures, and various birth defect stats. For hypothermia episodes, these probably would have no record at all if there were no hospital admissions–heat stroke would show up, but not heat exhaustion. Even then, making correlations requires matching up birth defects with heat stroke for individuals using personally identifiable information, rather than summary statistics. This can require permission from the patients, which can get expensive. So instead, people settle for proxies for the real data, like airport temperature for local temperature, (The latter would itself require tracking individuals and the expense thereof.) Limitations, such as neural tube defects that aren’t always documented, or airport temps as proxies for local temps, just have to be accepted, at least until there’s more money. Cataracts, which show up more easily, could act as a proxy to suggest (not show) birth defects. (Sometimes we have no choice but to use proxies, ever: our best data on the effects of radiation on humans comes from survivors of the Nagasaki and Hiroshima bombings. Since they weren’t wearing dosimeters, and we don’t want to repeat the experiment, all we have to represent their radiation dose is their location at the time of the blast.)
That this was a pilot study is, perhaps, suggested in the abstract:
If a pilot study shows interesting results, it can support an application to fund a larger study, that starts to take care of these problems, and make more direct measurements–To do the science “right.” The early results are still science, but their limitations must be ackowleged. For grant finding, statistical significance is not necessary if there’s good reason to believe that a larger sample size would give them. A result that fails to give significance can still be used to estimate statistical power (how likely you are to get a true positive if it’s there). Insufficient statistical power, often from too small a sample, can sink an NIH grant application.
Pilot studies can give data worthy of publication. This one didn’t seem to, though it’s not up to me to set editorial policy at a journal in a field I don’t work in. In any event, the data must be presented coherently and honestly, and competently, which didn’t happen here. Probably dull-witted authors and lax reviewers, probably, although crazy reviewers insisting on bizarre edits is always possible.
So the study, at least, can’t have been intended to draw really firm conclusions, and it didn’t. Reporting any such, much less as a connection to climate change is one more indicator of the demise of that undervalued, but valuable asset: the competent science reporter.
(For my procedure of translating the confidence intervals from p=0.05 to p=(0.05/28), I wanted to re-check my derivations and comment, but I’m too tired right now–hopefully in the next few days.)
JazzyT says:
December 25, 2012 at 9:20 pm
Thanks, Jazzy. In fact, we are not dividing 5/28, we are dividing 0.05 by 28, which is .0018, just as I had said above. And there’s a problem with your math, 5/28 is 0.13, not 0.013 as you say above …
No, JazzyT, they didn’t get anything resembling .002 significance. Had they done so, they would have plastered that fact all over their paper.
Why would it take “derivations” to find out that there is nothing there? Seems simple to me. Essentially, you move their whole claim off of the board, because they failed to find any significant results.
JazzyT, you seem to be missing two fundamental facts about this study.
First, it did not find anything. Nothing. Zero. Nada. Zilch. The results were exactly as would be predicted by random chance. In fact it found contradictory results, and relatively unexplainable results. One defect went up, one went down, and despite a claimed heat effect on congenital cataracts, there was no thermal effect on the neural tube defects known to be affected by heat … sounds random to me.
Second, it lacks a critical step in the logical chain. Their claim is that higher airport temperatures lead to congenital cataracts. Obviously there are two steps in the logical chain for that claim:
1) that high airport temperatures cause elevated fetal temperatures, and
2) that elevated fetal temperatures cause birth defects, particularly neural tube defects.
The second of these steps is uncontroversial. A number of studies have shown that high fetal temperatures can damage the fetus and cause congenital defects. There’s no need to prove that further, it is established.
That leaves the first link in the logical chain as the only unestablished step. This study could have been useful if they studied whether “heat waves” at the airport were connected with incidences of elevated fetal temperatures. If they could show that, then the game would be over, because the second link in the chain is already established.
You note this, but then you drop it (emphasis mine):
How could the causal chain be established “more rigorously” when it has not been established at all??? You keep talking like something has been established, but all we have in this study is totally random results. As a result, looking at the individuals is the only possible way that the study could be rescued. As Gertrude Stein remarked, “There’s no there there” regarding the study.
Actually, I don’t fault the science reporter in this one. I fault the authors, for hyping a non-result, and the journal, for either not noticing or not caring that they were hyping a non-result.
Finally, once again you are playing with the semantics. The problem is not that this study was not “intended to draw really firm conclusions”. That implies you could draw firm conclusions from the study, just not really firm conclusions … when in fact, you cannot draw the slightest conclusion from the study.
You’ve got to grasp the nettle, Jazzy. The study is a waste of electrons. It is no better than random chance, it reports unbelievable opposing results, and the authors are trying desperately to tapdance around that fact.
My best to you,
w.
Willis Eschenbach says:
December 25, 2012 at 11:51 pm
“The study is a waste of electrons. It is no better than random chance, it reports unbelievable opposing results, and the authors are trying desperately to tapdance around that fact.”
No,the paper should not have been published. The authors, editors, and reviewers may, individually or together, live to regret through professional embarrassment. And certainly, publishing an uncorrected data dredge is misleading. I don’t blame the reporters for being taken in, although I wish they could recognize something that looks like a pilot study and not get so excited about it.
With airport temps as a proxy for other environmentalt temps, I felt that discussions were on two tracks; one about how to make a really precise study one that would strongly establish the relationships between environmental temperatures and hyperthermia, with extensive records, instrumentation etc The other was more about epidemology in general, using the airport temperature method to illustrate cheap, quick and dirty methods to scrape some data together so as to say, “do we want to look into this some more?” High temps at the airport don’t cause hyperthermia elsewhere, but when someone outside suffers hyperthermia, it’s likely that its hot where they are, and usually a good bet that it’s hot at the nearest airport as well. (Then again, what they did in the paper was more complicated, perhaps better, but perhaps much worse,)
A run through the records may show an association of some kind. A closer look ma6 or may not show a strong association between two variables. This may be enough to be useful, but as we all know, it takes much more to really establish that one thing actually causes the other:
http://m.xkcd.com/552/